Engineering Review of Wind-Induced Torsional Moment and Response of Buildings

Alinejad, Hamidreza; Kang, Thomas H.-K.; Jeong, Seung Yong; Ahn, Byeonguk

doi:10.1061/JSENDH.STENG-12546

Open access

State-of-the-Art Reviews

Sep 12, 2023

Engineering Review of Wind-Induced Torsional Moment and Response of Buildings

Authors: Hamidreza Alinejad https://orcid.org/0000-0002-4616-2131 [email protected], Thomas H.-K. Kang, M.ASCE [email protected], Seung Yong Jeong [email protected], and Byeonguk Ahn [email protected]Author Affiliations

Publication: Journal of Structural Engineering

Volume 149, Issue 11

https://doi.org/10.1061/JSENDH.STENG-12546

PDF

Abstract

For building service and strength design under wind load, torsional moment and response (or torsional-wind load) is a main component. Several factors contribute to torsional-wind load, including asymmetric distribution of wind pressure on the building façade (aerodynamic source), dynamic torsional vibration, and the contribution of resonant components of along-wind and across-wind loads in presence of mass-stiffness eccentricity. In addition, adjacent building influence can be considerable. For low (1 or 2 stories) to midrise (less than 10 stories) buildings, the main component in torsional-wind load typically is aerodynamic source. For tall buildings, contribution due to all sources is significant. In this article, theoretical background and procedures to calculate torsional-wind load, with a focus on the concept of equivalent eccentricity and equivalent static wind load, are discussed. Then, procedures and perspectives in several international standards, including ASCE 7-22, Architectural Institute of Japan-recommendations for loads on buildings (AIJ-RLB-2015), Australian and New Zealand Standard (AS/NZS 1170.2-2011), Korean Design Standard (KDS 41-2019), and ISO 4354-2009, are introduced to clarify differing points of view and how components of torsional-wind load are included. Finally, the main parameters of each standard are compared with wind tunnel test results. The results confirm consistency between the wind tunnel test results and those based on the standards with consideration of their covered ranges.

Introduction

Torsional-wind load has a pronounced effect on building performance under both service and strength loads. The magnitude of torsional-wind load and its action, whether static or dynamic, is affected by several factors. Given that human perception is more sensitive to angular motion than translational, torsional acceleration can significantly affect building serviceability (Tallin and Ellingwood 1984; Kareem 1985). In addition, loading on peripheral members and cladding systems can be increased significantly, when torsional-wind load is considerable (Zhou et al. 2002). Moreover, neighboring buildings can influence change of pressure distribution and, consequently, torsional load.

When wind flow passes a building, three torsional moments can be applied to the structure: (1) torsional moment due to asymmetric distribution of wind pressure on building surfaces (aerodynamic component), (2) torsional moment (resonant component) due to induced torsional vibration in response to aerodynamic component, and (3) torsional moment due to contribution of inertial forces in along-wind and across-wind directions of structures with mass-stiffness eccentricity.

Aerodynamic components typically bear pivotal influence in short and medium-rise buildings. The role of induced-dynamic torsional component becomes significant for tall buildings, as the natural frequency of the building approaches the high-energy frequency content of the background load, where angular acceleration due to torsional vibration becomes noticeable. In addition, the existence of mass-stiffness eccentricity can considerably intensify the load.

These effects can be directly measured using an accurate finite element model and performing time-history analysis for aerodynamic wind load obtained by wind tunnel tests. However, the wind tunnel test results are not available at the early stage of design, and performing time-history analysis is not convenient for required trial and error at the design stage. Static analysis using equivalent static wind load (ESWL) is a more efficient approach for design. ESWL for torsion (hereinafter referred to as torsional-wind load) should be determined so as to be representative of all mentioned components. In wind engineering, the contribution of aerodynamic load is introduced using mean and background components, and the effect of dynamic response is introduced by resonant component. Moreover, depending on the applicable range in different standards, torsional-wind load is defined in quite different ways.

This article is part of a study on torsional-wind load, with the purpose of identifying key parameters that should be considered in determining torsional-wind load. Provisions and procedures in relevant standards include ASCE 7-22 (ASCE 2022), AS/NZS 1170.2-2011 (AS/NZS 2011), AIJ-RLB-2015 (AIJ 2015), ISO 4354-2009 (ISO 2009), and KDS 41-2019 (KDS 2019); they are hereinafter referred to as ASCE 7-22, AS/NZS, AIJ, ISO, and KDS, respectively. In addition, components of torsional-wind load were calculated based on results of wind tunnel tests for a set of buildings with a square-shaped plan and different heights, and comprehensively compared with the values from the standards.

Aerodynamic Load Effect

Aerodynamic torsional moment is due to asymmetric distribution of pressure on building surfaces (Fig. 1). The background component of along-wind load is primarily derived from the turbulence in (or gustiness of) the atmospheric boundary layer (ABL). The background component of across-wind load depends on turbulence in both ABL and the local boundary layer (LBL) formed between wind flow and the sidewalls, especially due to vortex shedding (Tamura et al. 1996). Mean and background components of aerodynamic torsional moment are due to the contribution of pressures acting on all walls, and thus, is a combination of turbulence in both ABL and LBL. Typically, the mean value of aerodynamic torsional moment for buildings with a symmetric plan is negligible when the wind direction is parallel to the symmetric line (Zhou and Kareem 2000); it is not necessarily true when the plan shape is not symmetrical or when the wind direction is not parallel to the symmetric line.

Fig. 1. Instantaneous pressure distribution on the walls of buildings at the moment of maximum aerodynamic: (a) along-wind load; (b) across-wind load; and (c) torsional-wind load. (Reprinted with permission from Tamura et al. 2008.)

Several factors may be considered as key factors included in the aerodynamic source, such as geometry of building, the wind flow incidence angle, mean wind speed, turbulence in ABL and LBL, and interference of adjacent building(s).

Across-wind load and torsional-wind load on buildings with large aspect ratios (

H / \sqrt{B D}

) are mainly induced by vortex shedding, where

B

,

D

, and

H

are width (normal to wind direction), length (parallel to wind direction), and height of the building, respectively. From the experimental results of Marukawa et al. (1992) and Ha et al. (2007), the separated vortices reattached to buildings when the side ratio (

D / B

) was larger than 3. Due to reattachment, the power spectral density (PSD) of across- and torsional-wind loads has two peaks. Note that based on observation by Marukawa et al. (1992), the PSD of torsional moment has two peaks at almost all side ratios, and the frequencies of the two peaks approach each other with increase in side ratio.

Studies by Blessmann and Riera (1985) and Blessmann (1992) identified that torsional-wind load can be highly affected by the interference effect. Research results by Zhang et al. (1995), Yu et al. (2016), and Hui et al. (2017) also indicate that torsional-wind load can be significantly larger than that of a building in an isolated condition. The effect of adjacent buildings, which may either decrease or increase aerodynamic forces, primarily depends on the geometry and arrangement of these structures, incident angle of wind flow, and upstream terrain conditions (Khanduri et al. 1998).

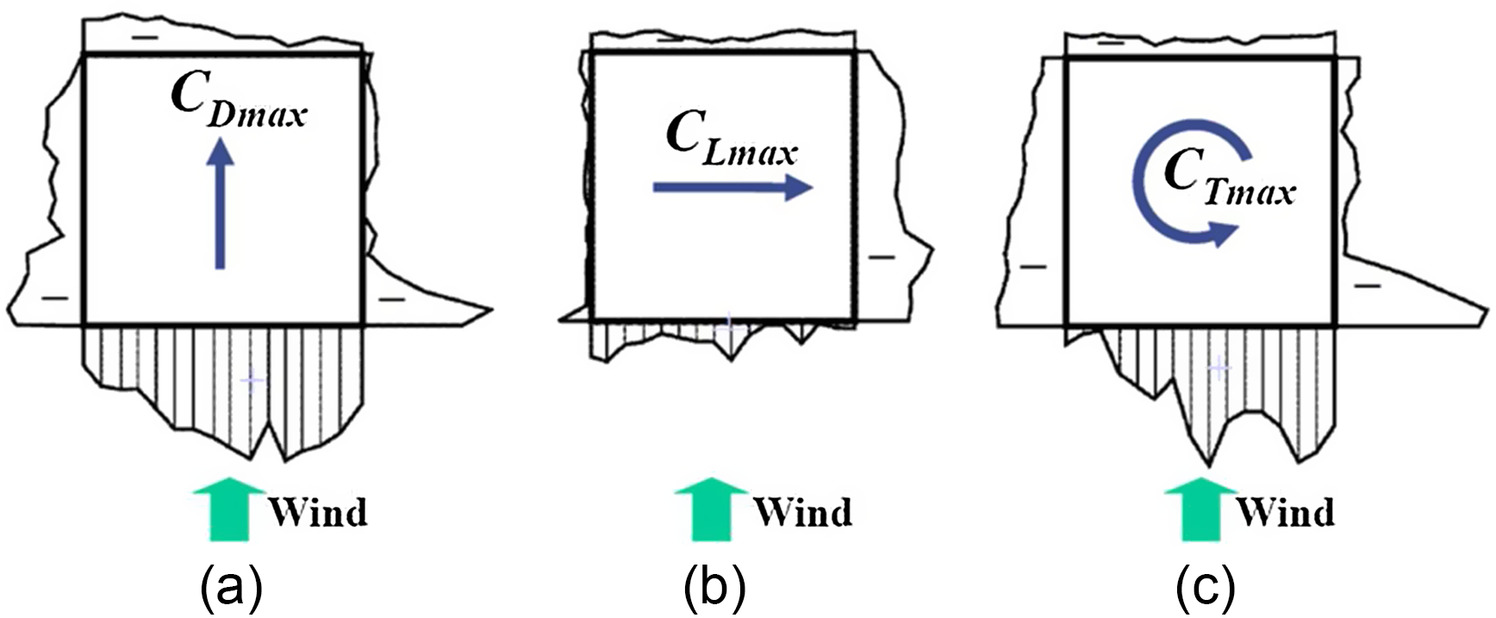
Dynamic Response Effect and Role of Mass-Stiffness Eccentricity

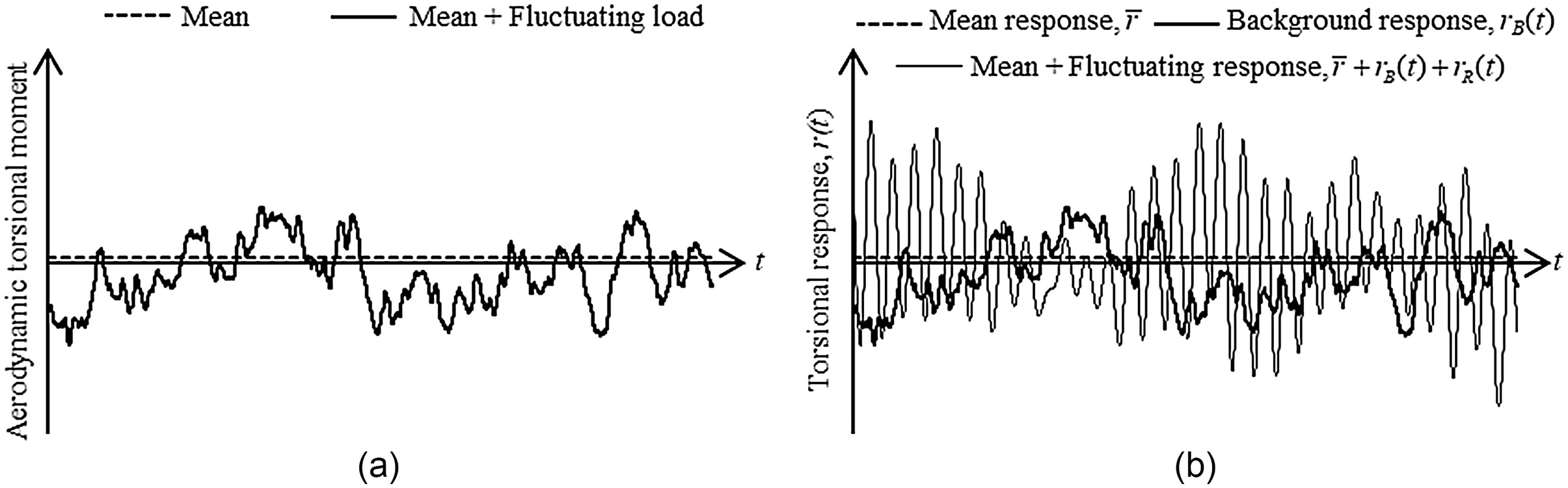
If the natural frequency of torsional mode is close to the high-energy frequency content of the aerodynamic load, the response can be significantly intensified due to inertial moment. The effect of dynamic response is introduced by resonant component in wind load. Fig. 2 illustrates the aerodynamic torsional moment and torsional response of the structure (e.g., rotation and base or story torsional moment) in the time domain. Aerodynamic torsional moment is composed of mean and background components. The total response is composed of mean (static response to mean load) and fluctuating components, where the fluctuating component is composed of background component (static response to fluctuating load) and resonant component (dynamic response to fluctuating load).

Fig. 2. (a) Aerodynamic torsional moment; and (b) torsional response.

The mean and background component of torsional-wind load is the summation of the torsional moment of pressure on the building surface with respect to a reference point (RP). The point can be considered at any arbitrary point of the floor plan, but is usually chosen at mass center (

C_{m}

), geometric center (

C_{g}

) (geometrical centroid of plan area), or elastic stiffness center (

C_{s}

). Regardless of the point selected, resonant components of along- and across-wind loads always form at mass center.

If

C_{m}

,

C_{g}

, and

C_{s}

are not the same, additional components are induced. Where

C_{m}

and

C_{s}

are not the same (i.e., mass-stiffness eccentricity), lateral and torsional modes of vibration are coupled. Although other cases of internal eccentricity (i.e., between

C_{m}

and

C_{g}

, or between

C_{s}

and

C_{g}

) do not result in coupling of lateral and torsional vibrations, their effect can also be significant for tall buildings. Study results by Tallin and Ellingwood (1985b), Kareem (1985), Saiful Islam et al. (1992), and Chen and Kareem (2005) showed that mass-stiffness eccentricity can change the overall load substantially.

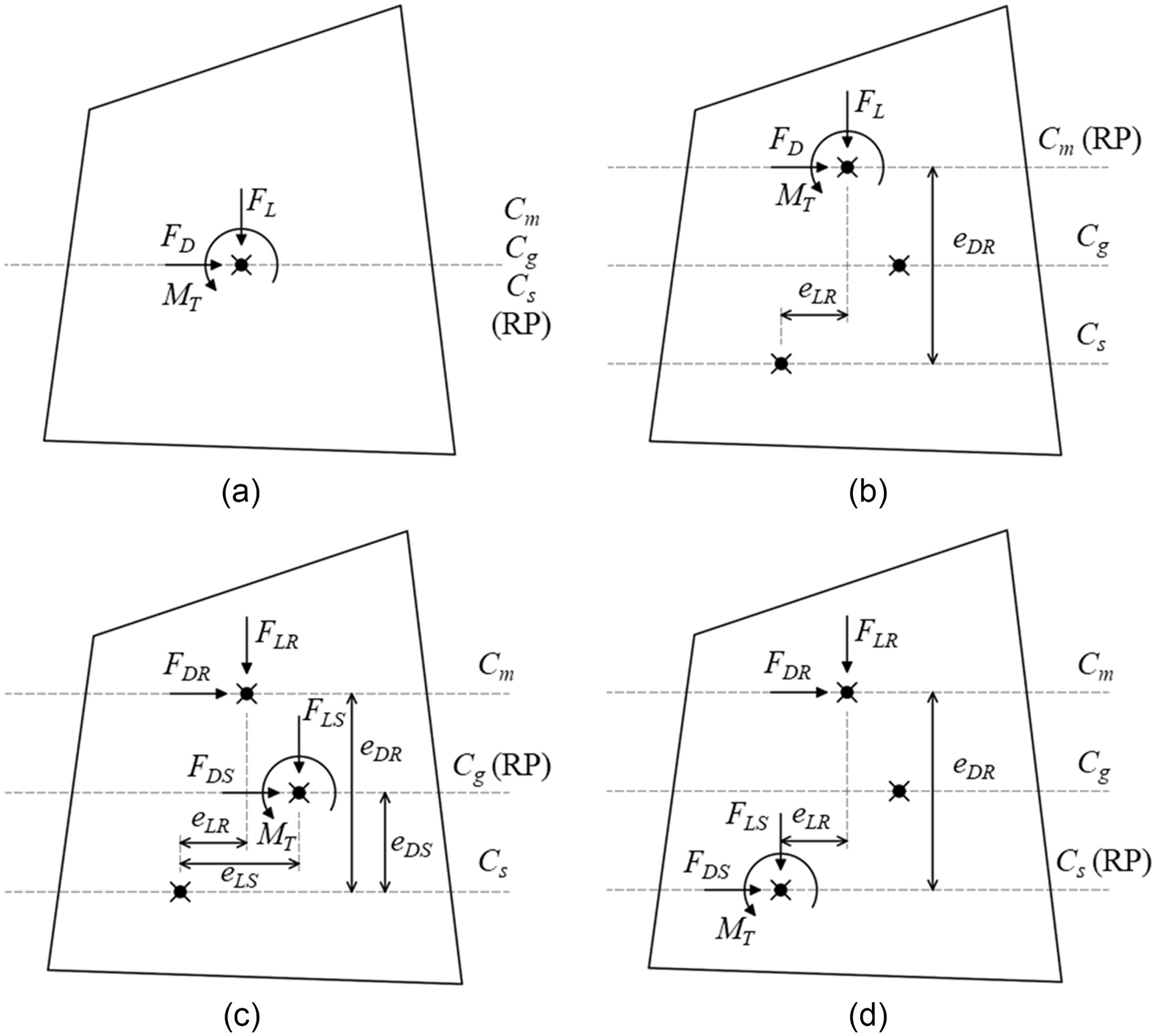
To illustrate possible eccentricities, four cases shown schematically in Fig. 3 for an arbitrary plan shape are considered. Here, total torsional-wind load (

M_{T T}

) acts at the center of stiffness and includes

M_{T}

(the summation of aerodynamic and dynamic torsional-wind moments) and the product of components

F_{D}

and

F_{L}

and their corresponding eccentricity. For the forces, the first subscripts

D

and

L

refer to along- and across-wind loads, respectively, and second subscripts

R

and

S

refer to resonant and the summation of mean and background (

F_{D S} = {\bar{F}}_{D} + F_{D B}

and

F_{L S} = {\bar{F}}_{L} + F_{L B}

), respectively. Eccentricities between centers of mass and stiffness are denoted by

e_{D R}

and

e_{L R}

, and eccentricities between centers of stiffness and geometry are denoted by

e_{D S}

and

e_{L S}

.

Fig. 3. Location of RP for an arbitrary plan shape: (a) at the center (the coincidence of $C_{g}$ , $C_{m}$ , and $C_{s}$ ); (b) at $C_{m}$ ; (c) at $C_{g}$ ; and (d) at $C_{s}$ .

A summary of the terms that should be considered in each case for calculation of

M_{T T}

is reported in Table 1. It is worth mentioning that floor behavior can be considered as a rigid diaphragm, which is common in analytical models of tall buildings. Hence, although the resonant component of

M_{T}

is also formed at the mass center, it is not necessary to decompose it into resonant component (

M_{T R}

) and aerodynamic component (

M_{T S}

).

Table 1. Contribution of components of

F_{D}

and

F_{L}

in

M_{T T}

due to eccentricity

Location of RP	Extra terms
Location of RP	Along-wind load	Across-wind load
Center^a	—	—
$C_{m}$	$e_{D R} F_{D}$	$e_{L R} F_{L}$
$C_{g}$	$e_{D S} F_{D S}$ , $e_{D R} F_{D R}$	$e_{L S} F_{L S}$ , $e_{L R} F_{L R}$
$C_{s}$	$e_{D R} F_{D R}$	$e_{L R} F_{L R}$

a

C_{g} = C_{m} = C_{s}

.

Mass-stiffness eccentricity may be inherent and accidental. In practice, even when a building is designed to have zero inherent eccentricity (zero eccentricity between centers of mass and stiffness), accidental eccentricity exists due to the nonuniform arrangement of mechanical, electrical and architectural components, construction error, etc. For this reason, consideration of accidental eccentricity in seismic design is recommended by codes and standards (e.g., 5% based on ASCE 7-22) where the load is essentially inertial force.

With regard to wind design, the resonant component (which is inertial force) in the case of short and medium-rise buildings is relatively small, and noninclusion of accidental eccentricity is reasonable. For tall buildings, the resonant component is generally large, especially for across-wind load, and even a small eccentricity can amplify the torsional-wind load. Hence, consideration of accidental eccentricity, as a minimum value for mass-stiffness eccentricity if inherent mass-stiffness is zero, for tall buildings can result in a safer design (Alinejad and Kang 2020b).

Evaluation of Torsional-Wind Load by Wind Tunnel Tests

Current wind tunnel tests can be divided into two categories: aeroelastic and aerodynamic. Aeroelastic wind tunnel tests are based on scaling of flow characteristics, geometry, and structural system; it is considered the most accurate available technique for the calculation of wind load, since all components including mean, background, and resonant are measured directly, and possible aeroelastic effects can be observed within the test. However, this test is expensive and preparation of the model is difficult and complex.

Aerodynamic wind tunnel tests are typically used in practice if the flow is not considerably affected by the building deformation and aeroelastic effects are not significant. Aerodynamic wind tunnel tests are based on scaling of flow characteristics and geometry, but structural properties are not included, and a rigid model is used. In the test, only aerodynamic components (mean and background) of the loads are measured, using high-frequency force balance or pressure integration techniques, and resonant component and contribution of mass-stiffness eccentricity should be obtained by performing numerical analysis.

For the calculation of torsional-wind load based on the result of aerodynamic wind tunnel tests, two approaches are considered.

In case of short and medium-rise buildings, across-wind load and resonant component of torsional-wind load are negligible. The mean and background components of along- and torsional-wind loads (

F_{D S}

and

M_{T S}

, respectively) are measured from the wind tunnel test as base shear and torsional moment with respect to center of geometry. Then, equivalent eccentricity (

e_{S}

) is representative of aerodynamic source of torsional-wind load and calculated as the ratio of

M_{T S \max} / (F_{D S \max} B)

, where

B

is projected width of building in the direction normal to wind direction, and

F_{D S \max}

and

M_{T S \max}

are the maximum values of

F_{D S}

and

M_{T S}

, respectively (Boggs et al. 2000; Isyumov and Case 2000; Elsharawy et al. 2012). If mass-stiffness eccentricity (

e_{R}

) is not zero, it should be considered for

F_{D R}

as an added term for torsional-wind load. To view the correlation between along- and torsional-wind loads, the load ratio is calculated as

F_{D S} (M_{T S \max}) / F_{D S \max}

, where

F_{D S} (M_{T S \max})

is the value of

F_{D S}

at the moment where

M_{T S} = M_{T S \max}

. This method is implemented in ASCE 7-22. Although the general procedure to obtain equivalent eccentricity is the same, sometimes slightly different assumptions are used (e.g., using

F_{D}

instead of

F_{D S}

for calculation of equivalent eccentricity).

For tall buildings, the condition is more complicated and both translational vibration in across-wind direction and torsional vibration are significant. In this condition, the procedure based on equivalent eccentricity is not suitable. Equivalent static torsional-wind load, comprising mean, background, and resonant components, can be a more realistic representation of wind-induced torsional effects. Because of the complexity associated with distribution of forces and torsional moment along with height, base forces and moments, in general, are measured and distributed based on fundamental mode shapes. Some models do not explicitly include turbulence intensity of ABL (Tamura et al. 1996; Li et al. 2014), while others include it (Liang et al. 2004; Katsumura et al. 2014).

Despite differences in the derivation of the equivalent static torsional-wind load, the load should be representative of aerodynamic load (mean and background loads) and dynamic response. The equivalent static load for the dynamic response (resonant load) is typically obtained based on either peak deformation or acceleration (Ryu et al. 2020). In current practice, with assumptions of negligible mean value and linear mode shape, equivalent static torsional-wind load based on measured torsional moment in wind tunnel tests is defined based on Eq. (1) (Tamura et al. 1996; Ha 2017; ISO 2009; AIJ 2015; KDS 2019)

M_{T} (z_{j}) = 3 g_{T} q_{H} (ϕ_{T 0} C_{T}^{'}) B A_{j} μ (z_{j}) \sqrt{1 + ϕ_{T} R_{T}}

(1)

where

z_{j}

= elevation of

j

th story;

g_{T}

= peak factor;

q_{H}

= velocity pressure at building height,

H

;

B

= width of building normal to wind direction;

A_{j} = B h_{j}

is the projected area normal to wind direction;

h_{j}

= height of

j

th story;

C_{T}^{'} = σ_{MTB} / (q_{H} H B^{2})

is the normalized

σ_{MTB}

, standard deviation of measured base torsional moment in wind tunnel;

R_{T} = {(σ_{MTR} / σ_{MTB})}^{2}

is the normalized

σ_{MTR}

, standard deviation of resonant response; and

μ (z) = {(z / H)}^{β}

is the mode shape. Also,

ϕ_{T}

is the mode correction factor for nonlinear mode shape and is usually defined as the ratio of the standard deviation or PSD of generalized load based on different mode shapes (Tallin and Ellingwood 1985a; Holmes 1987; Kijewski and Kareem 1998; Zhou and Kareem 2000; Zhou et al. 2002); and

ϕ_{T 0}

is the mode correction factor for generalized base torsion and is applied to

C_{T}^{'}

. This is used because measured base torsional moment in wind tunnel test is based on uniform mode shape (

β = 0

), while the load is based on linear mode shape (

β = 1

). In common practice, a value between 0.6 and 0.7 is used for

ϕ_{T 0}

in Marukawa et al. (1992), ASCE 49-21 (ASCE 2021), AIJ (2015), ISO (2009), and KDS (2019).

To calculate

R_{T}

,

σ_{MTR}

can be obtained by time-history analysis or by applying mechanical transfer function to the PSD of the base moment. In a case where a smooth PSD is available and the assumptions that the external load can be considered as white noise,

σ_{MTR}

can be estimated by

\sqrt{π f_{1 T} S_{MTB} (f_{1 T}) / 4 ξ_{1 T}}

, where

f_{1 T}

and

ξ_{1 T}

are the frequency and damping of the first torsional mode, respectively, and

S_{MTB} (f_{1 T})

is the value of PSD of base torsional moment at frequency of

f_{1 T}

(Lin 1967; Tallin and Ellingwood 1985b; Boggs and Dragovich 2006). The general procedure for obtaining equivalent static torsional-wind load based on wind tunnel test results is reported in Appendix I.

In the above procedure, it is assumed that there is no coupling between lateral and torsional mode shapes, and thus mass-stiffness eccentricity is zero. Several models were proposed to consider coupled mode shapes and the contribution of mass-stiffness eccentricity to torsional-wind load. Cui and Caracoglia (2018) proposed a universal formula based on a novel generalized aerodynamic formulation for calculating the coupled dynamic response of a tall building with consideration of aerodynamic damping and stiffness.

Exploring Torsional-Wind Load in Standards

In general, standards that include torsional-wind load can be divided in two categories, where the first group is based on equivalent eccentricity (ASCE 7-22 and AS/NZS) and the second group is based on computational procedure for calculation of equivalent static torsional-wind load (AIJ 2015; ISO 2009; KDS 2019). These procedures are explained in detail in the following subsections.

Procedure in ASCE 7-22 and AS/NZS

The provisions for wind design in ASCE 7-22 are provided mainly for short and medium-rise buildings with heights less than 122 m (150 m in practice) and cases that are not subject to vortex shedding and associated across-wind load. ASCE 7-22 does not provide an analytical equation for across-wind load by the vortex shedding. In addition, it is assumed that torsional vibration is not considerable. Hence, torsional-wind load,

M_{T}

, in ASCE 7-22 is defined based on contribution of aerodynamic torsional-wind load and resonant component of along-wind load (if mass-stiffness eccentricity is not zero). Therefore, it can be viewed that provisions in ASCE 7-22 are for short and medium-rise buildings, with wind tunnel tests required for tall buildings. Based on this code, the torsional-wind load for rigid and flexible buildings is defined by

M_{T} = e_{Q} B F_{D}

and

M_{T} = e B F_{D}

, respectively, where

B

is the width of building normal to wind direction,

e_{Q}

is eccentricity for rigid buildings, and

e

is eccentricity for flexible buildings. Based on results of aerodynamic wind tunnel tests, the measured

e_{Q}

for the rigid building is about 0.15.

Note that

e_{Q}

is the equivalent eccentricity introduced in the section “Evaluation of Torsional-wind Load by Wind Tunnel Tests.” Eccentricity for the flexible building is calculated by using the following equation:

e = \frac{e_{Q} + 1.7 I_{\bar{z}} \sqrt{{(g_{Q} Q e_{Q})}^{2} + {(g_{R} R e_{R})}^{2}}}{1 + 1.7 I_{\bar{z}} \sqrt{{(g_{Q} Q)}^{2} + {(g_{R} R)}^{2}}}

(2)

where

Q

and

R

= background and resonant factors, respectively;

I_{\bar{z}}

= turbulence intensity at equivalent height (60% of building height);

g_{Q}

and

g_{R}

= peak factors for background and resonant forces, respectively; and

e_{R}

= eccentricity between mass and stiffness center.

It is worth noting that accidental eccentricity can be simply included in ASCE 7-22 by directly adding its value to

e_{R}

. Based on the results of Alinejad and Kang (2020a), variation of

e

as a function of building time period, damping ratio,

e_{R}

, and wind speed is shown schematically in Fig. 4.

Fig. 4. Variation of eccentricity in ASCE 7.

When

R

is zero (i.e., for rigid buildings), Eq. (2) is reduced simply to

e_{Q}

. However, for flexible buildings (with nonzero

R

) with

e_{R} = 0

, the value of

e

is smaller than

e_{Q}

. The reason is that

M_{T}

is calculated based on

F_{D}

(including its mean, background, and resonant components). However, mean and background are multiplied by

e_{Q} B

and resonant component by

e_{R} B

. Hence, when the resonant component is not zero but

e_{R}

is zero,

e

is smaller to adjust the required correction for exclusion of the resonant component. Thus, the value of

e

is smaller for a larger

R

component (due to higher wind speed, longer period of the structure, and smaller damping ratio). For cases with non-zero

e_{R}

but less than

e_{Q}

, the value of

e

is also less than

e_{Q}

. By subtracting

e_{Q}

from the numerator, the multiplier of

R

would be

e_{R} / e_{Q}

, with the multiplier in the denominator being 1. Hence, the value of

e

is always less than

e_{Q}

, unless

e_{R}

is larger than

e_{Q}

. When

e_{R}

is larger than

e_{Q}

for a larger

R

component, the value of

e

is larger. For better understanding of the above observation, the procedure to derive Eq. (2) is provided in Appendix II.

To consider the maximum impact of the wind load on the structure, four load cases are defined by ASCE 7-22, as shown in Table 2. Case 2 and Case 4 are for the combination of along- and torsional-wind loads. Case 3 and Case 4 identified in the table are for the maximum load effect scenario when the wind load acts in a diagonal direction. Based on wind tunnel tests of a rigid building, the peak torsional-wind load is equivalent to the case where 15% eccentricity exists for a portion of peak along-wind load. It occurs at about 75% of the peak along-wind load. Thus, a reduction factor of 0.75 is included for Case 2 and Case 4.

Table 2. Combination of along- and torsional-wind loads in ASCE 7-22

Case	$F_{D}$	$M_{T}$	Eccentricity, $e$ ^a
1	$F_{D X}$	—	—
1	$F_{D Y}$	—	—
2	$0.75 F_{D X}$	$0.75 e_{X} F_{D X}$	$e_{X} = \pm e B_{X}$
2	$0.75 F_{D Y}$	$0.75 e_{Y} F_{D Y}$	$e_{Y} = \pm e B_{Y}$
3	$0.75 F_{D X}$ $+$ $0.75 F_{D Y}$	—	—
4	$0.563 F_{D X}$ $+$ $0.563 F_{D Y}$	$0.563 e_{X} F_{D X} + 0.563 e_{Y} F_{D Y}$	$e_{X} = \pm e B_{X}$ , $e_{Y} = \pm e B_{Y}$

Note: $F_{D X}$ and $F_{D Y}$ are the wind force $F_{D}$ corresponding to $x$ and $y$ directions, respectively; $B_{X}$ and $B_{Y}$ are the widths of building normal to $x$ and $y$ axes, respectively; $e_{X}$ and $e_{Y}$ are the eccentricities for $x$ and $y$ axes, respectively.

a

e_{Q}

is used for rigid building in lieu of

e

.

Based on AS/NZS, torsional-wind load should be included based on 20% eccentricity with respect to the center of geometry of the building on the along-wind load for rectangular buildings taller than 70 m. It is also required where the plan aspect ratio is larger than 1.5, due to the influence of across- and torsional-wind loads. In contrast to ASCE 7-22, the eccentricity in AS/NZS is applied to all components of along-wind load (mean, background, and resonant components). In addition, the eccentricity should be used for medium-rise to tall buildings, and thus includes torsional vibration (resonant component). Based on the evaluation by Alinjead et al. (2020), the ratio of torsional-wind load (including resonant component) and along-wind load for buildings with height of 80 to 200 m and different wind speeds varies between 0.11 to 0.24. Therefore, a value of 0.2 for eccentricity can be considered a logical value for the estimation of torsional-wind load.

Procedure in AIJ, ISO, and KDS

In addition to wind load provisions for short and medium-rise buildings, AIJ, ISO, and KDS provide procedures to calculate across- and torsional-wind loads for tall buildings with a rectangular plan for a range of wind speeds and building properties (Table 3).

Table 3. Covered range by AIJ, ISO, and KDS

Item	Covered range
Plan section	Uniform rectangular
Height to plan aspect ratio	$3 \leq \frac{H}{\sqrt{B D}} \leq 6$
Plan aspect ratio	$0.2 \leq \frac{D}{B} \leq 5$
Wind speed and natural frequency	$\frac{V_{H}}{f_{1 L} \sqrt{B D}} \leq 10$ and $\frac{V_{H}}{f_{1 T} \sqrt{B D}} \leq 10$

Note: $H$ = building height; $B$ and $D$ = width of building normal and parallel to wind direction, respectively; $V_{H}$ = wind speed at building height; and $f_{1 L}$ and $f_{1 T}$ = fundamental natural frequency in across and torsional modes of vibration, respectively.

Torsional-wind loads in these standards are obtained based on the procedure explained in the section “Evaluation of Torsional-Wind Load by Wind Tunnel Tests” and by the format of Eq. (1) (Ha 2017). With assumption of negligible mean component and only consideration of background component (

M_{T B}

) and resonant component (

M_{T R}

), torsional-wind load is defined in the form of

M_{T} = \sqrt{M_{T B}^{2} + M_{T R}^{2}}

. The definition of

M_{T B}

and

M_{T R}

in each code is provided in Table 4.

Table 4. Definition of background and resonant component in AIJ, ISO, and KDS

Code	Background components ( $M_{T B}$ )	Resonant component ( $M_{T R}$ )
AIJ	$1.8 g_{T} C_{T}^{'} q_{H} B A_{j} (\frac{z_{j}}{H})$	$1.8 g_{T} C_{T}^{'} q_{H} B A_{j} ϕ_{T} {(\frac{z_{j}}{H})}^{β} \sqrt{R_{T}}$
ISO	$3 g_{T} C_{T}^{'} q_{H} B A_{j} {(\frac{z_{j}}{H})}^{β}$	$3 g_{T} C_{T}^{'} q_{H} B A_{j} K {(\frac{z_{j}}{H})}^{β} \sqrt{R_{T}}$
KDS	$1.8 g_{T} C_{T}^{'} q_{H} B A_{j} (\frac{z_{j}}{H})$	$1.8 g_{T} C_{T}^{'} q_{H} B A_{j} (\frac{z_{j}}{H}) \sqrt{R_{T}}$

Note: $q_{H}$ = pressure velocity at building height; $B$ and $H$ = width and height of the building, respectively; $z_{j}$ , $h_{j}$ , and $A_{j}$ = elevation, height, and area normal to wind direction ( $= B h_{j}$ ) of $j$ th story, respectively; $C_{T}^{'}$ = normalized standard deviation of torsional moment fluctuation; $g_{T}$ = peak factor in torsional-wind load; $R_{T}$ = resonant response factor for torsional-wind load; $K$ and $ϕ_{T}$ = mode shape correction factors; and $β$ = exponent of power law for the first mode vibration shape.

Peak factor in torsional-wind load,

g_{T}

, based on ISO, is defined by Eq. (3), and for AIJ and KDS by Eq. (4). The values from both equations are almost the same

g_{T} = \sqrt{2 \ln (600 f_{1 T})} + \frac{0.577}{\sqrt{2 \ln (600 f_{1 T})}}

(3)

g_{T} = \sqrt{2 \ln (600 f_{1 T}) + 1.2}

(4)

where

f_{1 T}

= natural frequency of the first mode of torsional vibration.

In contrast to KDS, the mode shape correction factor for nonlinear mode shape is included in AIJ and ISO (

K

and

ϕ_{T}

, respectively);

K

and

ϕ_{T}

are defined by

0.27 β + 0.73

and

I_{T 1} / I_{T} (1 - 0.4 \ln β)

, respectively, where

β

is the exponent of power-law for the first torsional vibration mode,

I_{T}

is the generalized mass of building for torsional vibration, and

I_{T 1}

is the value of

I_{T}

for linear mode shape (i.e.,

β = 1

). Values of

K

and

ϕ_{T}

are very close to each other for

β

in the range of 0.1 to 2.

Resonant response factor for torsional vibration,

R_{T}

, is defined by

π F_{T} / (4 ξ_{1 T})

, where

ξ_{1 T}

is the damping ratio of the first mode of torsional vibration and

F_{T}

is the coefficient of spectrum in torsional vibration.

Procedures to calculate

F_{T}

in ISO and KDS are the same (Table 5), while in AIJ the procedure differs (Table 6).

Table 5. Definition of

F_{T}

and its related parameters in ISO and KDS

Parameter	Content
Coefficients of spectrum in torsional vibration	$\begin{array}{l} F_{T} = \frac{0.14 K_{T}^{2} {(V_{T}^{})}^{2 β_{T}}}{π} \frac{D {(B^{2} + D^{2})}^{2}}{L_{D B}^{2} B^{3}} & V_{T}^{} \leq 4.5 or 6 \leq V_{T}^{} \leq 10 \\ F_{T} (V_{T}^{} = 4.5) = F_{4.5} and F_{T} (V_{T}^{} = 6) = F_{6} \\ F_{T} = F_{4.5} \exp [3.5 \ln (\frac{F_{6}}{F_{4.5}}) \ln (\frac{V_{T}^{}}{4.5})] & 4.5 < V_{T}^{*} < 6 \end{array}$
Amplification factor for torsional vibration spectrum	$K_{T} = {\begin{cases} \frac{- 1.1 (D / B) + 0.97}{{(D / B)}^{2} + 0.85 (D / B) + 3.3} + 0.17 & V_{T}^{} \leq 4.5 \\ \frac{0.077 (D / B) - 0.16}{{(D / B)}^{2} - 0.96 (D / B) + 0.42} + \frac{0.35}{(D / B)} + 0.095 & 6 \leq V_{T}^{} \leq 10 \end{cases}$
Exponential factor for the normalized wind speed for torsional vibration	$K_{T} = {\begin{cases} \frac{(D / B) + 3.6}{{(D / B)}^{2} - 5.1 (D / B) + 9.1} + \frac{0.14}{D / B} + 0.14 & V_{T}^{} \leq 4.5 \\ \frac{0.44 {(D / B)}^{2} - 0.0064}{{(D / B)}^{4} - 0.26 {(D / B)}^{2} + 0.1} + 0.2 & 6 \leq V_{T}^{} \leq 10 \end{cases}$
Normalized wind speed for the torsional vibration	$V_{T}^{*} = \frac{V_{H}}{f_{1 T} \sqrt{B D}}$

Note: $B$ and $D$ = widths of building normal and parallel to wind direction, respectively; $L_{D B}$ = greater value of $D$ and $B$ ; $V_{H}$ = wind speed at building height; and $f_{1 T}$ = fundamental natural frequency in torsional mode of vibration.

Table 6. Definition of

F_{T}

and its related parameters in AIJ

Parameter	Content
Coefficients of spectrum in torsional vibration	$F_{T} = 0.8 F_{B} + v_{1} F_{V} + w_{1} F_{W}$
Component of $F_{T}$ due to approach flow and turbulence created by the building^a	$F_{B} = \frac{18 f_{m}^{}}{{(1 + 0.46 {(18 f_{m}^{})}^{1.8})}^{2.3}}$
Component of $F_{T}$ due to vortex shedding^a	$F_{V} = \frac{1}{v_{2} \sqrt{2 π}} \exp (- 0.5 {(\frac{\ln (f_{s}^{*} / v_{3}) + 0.5 v_{2}^{2}}{v_{2}})}^{2})$
Component of $F_{T}$ due to reattachment^a	$F_{W} = \frac{1}{w_{2} \sqrt{2 π}} \exp (- 0.5 {(\frac{\ln (f_{m}^{*} / w_{3}) + 0.5 w_{2}^{2}}{w_{2}})}^{2})$
Amplification factor for $F_{V}$	$v_{1} = {\begin{cases} - 2 ({(D / B)}^{2} - (D / B)) & D / B \leq 0.9 (* * 1.0) \\ 0.1 {(D / B)}^{- 1} & D / B > 0.9 (* * 1.0) \end{cases}$
Factor related to $F_{V}$	$v_{2} = {\begin{cases} 0.56 I_{H} {(D / B)}^{- 1} & D / B \leq 0.9 (* * 1.0) \\ 2 I_{H} {(D / B)}^{0.5} & D / B > 0.9 (* * 1.0) \end{cases}$
Factor related to $F_{V}$	$v_{3}^{* } = {\begin{cases} 0.8 {(D / B)}^{- 0.2} & D / B \leq 0.9 ( * 1.0) \\ 0.18 (D / B) & D / B > 0.9 (* * 1.0) \end{cases}$
Amplification factor for $F_{W}$	$w_{1} = {\begin{cases} 0.04 {(D / B)}^{- 0.5} & D / B \leq 0.9 (* * 1.0) \\ 0.06 & D / B > 0.9 (* * 1.0) \end{cases}$
Factor related to $F_{W}$	$w_{2} = {\begin{cases} 1.75 \sqrt{I_{H}} & D / B \leq 0.9 (* * 1.0) \\ 0.7 \sqrt{I_{H}} & D / B > 0.9 (* * 1.0) \end{cases}$
Factor related to $F_{W}$	$w_{3} = 0.24 {(D / B)}^{- 0.4}$
Nondimensional frequency for $F_{B}$ and $F_{W}$	$f_{m}^{*} = \frac{f_{1 T} B}{V_{H}}$
Nondimensional frequency for $F_{V}$	$f_{s}^{*} = \frac{8.3 f_{1 T} B {(1 + 0.38 {(D / B)}^{1.5})}^{0.89}}{V_{H}}$

Note: $B$ and $D$ = widths of building normal and parallel to wind direction, respectively; $V_{H}$ = wind speed at building height; $I_{H}$ = turbulence intensity at building height; and $f_{1 T}$ = fundamental natural frequency in torsional mode of vibration.

a

Definitions were taken from Katsumura et al. (2014).

C_{T}^{'}

is equal to

σ_{MTB} / (q_{H} H B^{2})

, where

σ_{MTB}

is the standard deviation of base torsional moment fluctuation, and its definitions based on listed standards are provided in Table 7.

Table 7. Definition of

C_{T}^{'}

in AIJ, ISO, and KDS

Standard	Content
AIJ	$C_{T}^{'} = 0.04 {(D / B)}^{2} + 0.02$
KDS	$C_{T}^{'} = {0.0066 + 0.015 {(D / B)}^{2}}^{0.78}$
ISO	$C_{T}^{'} = {0.0034 + 0.0078 {(D / B)}^{2}}^{0.78}$

Note: $B$ and $D$ = widths of building normal and parallel to wind direction, respectively.

Derivation of procedures in these standards is more-or-less similar to the method described in the section “Evaluation of Torsional-Wind Load by Wind Tunnel Tests.” In these standards, torsional-wind load is calculated based on linear mode shape with a correction factor for generalized base torsion,

ϕ_{T 0}

, equal to 0.6. In ISO, the standard deviation is multiplied by the factor and directly included in

C_{T}^{'}

, while in AIJ and KDS it is included in the multiplier of the load (

3 \times 0.6 = 1.8

). The values of

C_{T}^{'}

in ISO (after applying

ϕ_{T 0} = 0.6

) and KDS are similar to that in the former version of AIJ (AIJ 2004), whereas for AIJ, a fitted function developed by Katsumura et al. (2014) is introduced for

C_{T}^{'}

.

Load case combinations for along-, across-, and torsional-wind loads based on AIJ, ISO, and KDS are listed in Table 8.

Table 8. Combination of along-, across-, and torsional-wind loads in AIJ, ISO, and KDS

Load case	$F_{D}$			$F_{L}$			$M_{T}$
Load case	AIJ	ISO	KDS	AIJ	ISO	KDS	AIJ	ISO	KDS
1	1			0.4			0.4
2	$0.4 + \frac{0.6}{G_{D}}$			1			$\sqrt{2 + 2 ρ_{L T}} - 1$	$κ$
3	$0.4 + \frac{0.6}{G_{D}}$			$\sqrt{2 + 2 ρ_{L T}} - 1$	$κ$		1

Note: $F_{D}$ , $F_{L}$ , and $M_{T}$ = along-, across-, and torsional-wind loads, respectively; $G_{D}$ = gust-effect factor (mean dynamic response factor for $F_{D}$ in ISO); and $κ$ and $ρ_{L T}$ = wind load combination factors and correlation coefficient for across- and torsional-wind load.

The values of factors for combining across- and torsional-wind loads (

κ

and

ρ_{L T}

) shown in Table 8 are listed in Tables 9 and 10. Overall, AIJ considers larger load combination factors for buildings with smaller plan aspect ratios (

D / B

).

Table 9. Combination factor for across- and torsional-wind loads,

κ

, of ISO and KDS

$D / B$	$n_{1} B / V_{H}$	$κ$
$\leq 0.5$	0.1	0.55
	0.2	0.65
	0.6	0.8
1	0.1	0.55
	0.3	0.55
	0.6	0.65
$\geq 2$	—	0.55

Note = For intermediate values of $D / B$ and $n_{1} B / U_{H}$ , linear interpolation can be used. $B$ and $D$ = widths of building normal and parallel to wind direction, respectively; $V_{H}$ = wind speed at building height; and $n_{1}$ = smaller of natural frequency in first translational mode in across-wind direction ( $f_{1 L}$ ) and first torsional mode ( $f_{1 T}$ ).

Table 10. Correlation coefficient for across- and torsional-wind loads,

ρ_{LT}

, of AIJ

$D / B$	$n_{1} B / V_{H}$	$ρ_{LT}$			$\sqrt{2 + 2 ρ_{LT}} - 1$
$D / B$	$n_{1} B / V_{H}$	$ζ = 1.0$	$ζ = 1.1$	$ζ \geq 1.4$	$ζ = 1.0$	$ζ = 1.1$	$ζ \geq 1.4$
$\leq 0.5$	$\leq 0.1$	0.9	0.7	0.5	0.95	0.84	0.73
	0.2	0.3	0.6	0.5	0.61	0.79	0.73
	0.3	0.4	0.6	0.6	0.67	0.79	0.79
	0.6	0.6	0.6	0.6	0.79	0.79	0.79
	$\geq 1$	0.7	0.7	0.7	0.84	0.84	0.84
1	$\leq 0.1$	0.8	0.5	0.2	0.90	0.73	0.55
	0.2	0.6	0.5	0.5	0.79	0.73	0.73
	$\geq 0.3$	0.5	0.5	0.5	0.73	0.73	0.73
$\geq 2$	$\leq 0.05$	0.6	0.4	0.3	0.79	0.67	0.61
	0.1	0.6	0.2	0.2	0.79	0.55	0.55
	$\geq 0.2$	0.2	0.2	0.2	0.55	0.55	0.55

Note = For intermediate values of $D / B$ , $ζ$ , and $n_{1} B / V_{H}$ , linear interpolation can be used. $B$ and $D$ = widths of building normal and parallel to wind direction, respectively; $V_{H}$ = wind speed at building height; $n_{1}$ = smaller of natural frequency of first translational mode in across-wind direction ( $f_{1 L}$ ) and first torsional mode ( $f_{1 T}$ ); and $ζ = f_{1 L} \geq f_{1 T} ζ = f_{1 L} / f_{1 T}$ , $f_{1 L} < f_{1 T} ζ = f_{1 T} / f_{1 L}$ .

In the derivation of the load combinations in these standards, it is assumed that the response can be expressed by the normal distribution, which can be attributed to the significant contribution of resonance response for tall buildings with small natural frequencies. Responses in two directions,

M_{x}

and

M_{y}

, are expressed through a 2D normal distribution, where

M_{x}

and

M_{y}

can be base overturning or torsional moments, respectively. In this condition, the equivalence line of probability becomes an elliptical line using the correlation coefficient of the response,

ρ

, as shown in Fig. 5 (Solari et al. 1998; Solari and Pagnini 1999). Given that the probability of any design point (a combination of

M_{x}

and

M_{y}

) outside of the ellipse is small, all points on the elliptical line (solid line) can be considered as a load combination. However, it is impractical to consider all load combinations. Therefore, load combinations, based on the model proposed by Asami (2000), are defined with eight points on the apexes of the enveloping octagon. In this model, the moment in

y

-direction (

M_{y c}

) to be combined with the maximum moment in

x

-direction (

M_{x \max}

) is defined by

M_{y c} = {\bar{M}}_{y} + m_{y \max} (\sqrt{2 + 2 ρ} - 1)

(5)

where

{\bar{M}}_{y}

and

m_{y \max}

= mean and the maximum of fluctuating component of the moment in the

y

-direction; and

ρ

= correlation coefficient between

M_{x}

and

M_{y}

. Regarding the components of wind load,

ρ

is defined as

ρ_{D L}

(correlation coefficient between along- and across-wind loads),

ρ_{D T}

(correlation coefficient between along- and torsional-wind loads), and

ρ_{L T}

(correlation coefficient between across- and torsional-wind loads).

Fig. 5. Schema of AIJ load combination in consideration of response correlation.

The correlation factor for across- and torsional-wind loads (

κ

and

ρ_{L T}

) is defined based on (1) co-coherence (correlation coefficient for each frequency) between along- and across-wind loads and also between along- and torsional-wind loads being negligible, i.e.,

ρ_{D L}

and

ρ_{D T}

are zero; and co-coherence between across- and torsional-wind loads not being zero, where the absolute value of the correlation coefficient of response,

ρ_{L T}

, is defined based on wind tunnel tests.

Factors for along-wind load,

F_{D}

, in load cases 2 and 3 are obtained as follows. Because

ρ_{D L}

and

ρ_{D T}

are zero, the value inside the parenthesis in Eq. (5) is equal to roughly 0.4. By replacing

M_{y c}

with components of

F_{D}

(

= {\bar{F}}_{D} + F_{D \max}^{'}

, i.e., summation of mean and maximum fluctuation component, respectively), Eq. (5) can be written as

F_{D} = {\bar{F}}_{D} + 0.4 F_{D \max}^{'}

. Substituting

{F^{'}}_{D \max}

by

F_{D} - {\bar{F}}_{D}

and considering the definition of along-wind load,

F_{D} = G_{D} {\bar{F}}_{D}

, it is further modified as

F_{D} (0.4 + 0.6 / G_{D})

.

In case of across- (

F_{L}

) and torsional-wind (

M_{T}

) loads, the mean term in Eq. (5) is zero. Therefore, the factors of 0.4 for both of

F_{L}

and

M_{T}

in load case 1 are obtained by considering zero

ρ_{D L}

and

ρ_{D T}

. Similarly, the factors for load cases 2 and 3 are obtained by replacing

ρ

with

ρ_{L T}

.

If damping ratio,

ξ

, is sufficiently small, the steady-state response of structure,

u (t)

, with natural frequency,

f_{n}

, under external sinusoidal force (with the frequency of

f

) can be calculated by Eqs. (6)–(8) (Chopra 2017)

u (t) = u_{s t 0} R_{d} \sin (2 π f t - ϕ)

(6)

R_{d} = {(\sqrt{{[1 - {(f / f_{n})}^{2}]}^{2} + {[2 ξ (f / f_{n})]}^{2}})}^{- 1}

(7)

ϕ = \tan^{- 1} \frac{2 ξ (f / f_{n})}{1 - {(f / f_{n})}^{2}}

(8)

where

{(u_{s t})}_{o}

= maximum value of static deformation;

R_{d}

= deformation response factor; and

ϕ

= phase lag. Regardless of natural frequency, the responses can be considered as sinusoidal functions with frequency of load. Aerodynamic wind loads are wideband processes and can be decomposed into a summation of sinusoidal functions with different frequencies. The total response of a linear system to aerodynamic wind load is the combination of the responses to harmonic loads corresponding to each frequency content of the load. If resonant response is very significant and the governing response, the contribution of response from the harmonic load with the frequency equal to natural frequency, will be significantly larger than other frequencies. In this condition, overall response can be assumed as a single harmonic response with the natural frequency, especially for across-wind and torsional response.

Consider two resonant responses

X (t) = A_{X} \cos (2 π f_{X} t)

and

Y (t) = A_{Y} \cos (2 π f_{Y} t + θ)

with natural frequencies of

f_{X}

and

f_{Y}

, respectively, where

A_{X}

and

A_{Y}

are amplification factors for the two resonant responses, respectively, and

θ

is phase difference between

X (t)

and

Y (t)

. Here,

X (t)

and

Y (t)

may be across- and torsional-wind responses. It can be shown that covariance between

X (t)

and

Y (t)

can be derived by using Eq. (9)

Cov (X (t), Y (t)) = E [(A_{X} \cos (2 π f_{X} t)) (A_{Y} \cos (2 π f_{Y} t + θ))] = \frac{A_{X} A_{Y}}{2} (E [\cos (2 π (f_{X} - f_{Y}) t - θ)] + E [\cos (2 π (f_{X} + f_{Y}) t + θ)])

(9)

where

E [\cdot]

= the expected value. Because

f_{X}

and

f_{Y}

are positive values, the right expectation is equal to zero. However, the left expectation is equal to zero if

f_{X}

and

f_{Y}

are not equal. Thus, unless

f_{X}

and

f_{Y}

are the same, the covariance between

X (t)

and

Y (t)

is zero, and the resultant correlation coefficient is also zero. In practice, natural frequency in torsional mode of vibration is not the same as that of translational modes. Natural frequency of torsional mode in ISO was assumed to be around 1.3 to 1.4 times those of translation modes. Thus, if torsional mode is not coupled with translational modes, it can be assumed that the correlation coefficient between torsional-resonant response and both along- and across-resonant responses is zero. On the other hand, for background components, if original two aerodynamic wind loads are correlated at a specific frequency, the background responses are still correlated, provided that contribution of phase lags,

ϕ

, by natural frequencies is not significant. However, amplitudes of background responses are negligible compared with resonant responses. Consequently, a value of 0.4 can be used instead of an exact value of

κ

.

The values of

κ

(= \sqrt{2 + 2 ρ} - 1)

in ISO and KDS are also calculated following a similar procedure.

Values of

ρ_{L T}

in Table 10 for AIJ are obtained based on time-history analysis (AIJ 2015; Somekawa et al. 2014), while the values of

κ

in ISO and KDS are calculated by the statistical analysis method (Asami 2000). In all cases, analysis is done under a specific range of damping ratios (e.g., 0.01–0.05) and the assumption that the building has no coupling vibration mode (i.e., zero eccentricity). Hence, provisions are not applicable when the damping factor is not in the range, or if the vibration mode of the building is significantly coupled (i.e., nonzero eccentricity).

Based on ISO, if the building has some eccentricity, a more detailed examination should be made for the wind-load combinations; whereas, in AIJ, buildings with an eccentricity (eccentric distance/radius of rotation) of 0.15 or less (i.e.,

e_{R} \leq 0.15

) are subject to the estimation equation. However, the wind load on a building for which eccentricity cannot be ignored needs to be calculated based on the results of wind tunnel tests or computational fluid dynamics (CFD).

Comparison with Results of Wind Tunnel Tests

Tokyo Polytechnic University (TPU) provides an open-access aerodynamic database for high-rise buildings (Tamura 2012), which includes results of pressure integration tests on 1/400 scaled rigid rectangular prism models with different heights, side ratios (

D / B

), exposure types, and angles of attack. Sampling frequency and duration of all tests are 1,000 Hz and 32.768 s, respectively. For the purpose of this study, wind pressure data were extracted for buildings with aspect ratio (

height ∶ breadth ∶ depth

) of

2 ∶ 1 ∶ 1

,

3 ∶ 1 ∶ 1

,

4 ∶ 1 ∶ 1

, and

5 ∶ 1 ∶ 1

(which correspond to buildings with width of 40 m and height of 80, 120, 160, and 200 m in real scale); the sample included urban and suburban areas with wind speed profile power (exposure factor),

α

, of 1/4 and 1/6, respectively, and 0° to 45° angle of attack. Information regarding dimensions of specimens and wind speeds in the wind tunnel test is summarized in Table 11.

Table 11. Wind tunnel information

Model dimensions		Averaged wind speed at building height ( $m / s$ )
$H$ (m)	$B = D$ (m)	$α = 1 / 4$	$α = 1 / 6$
0.2	0.1	10.97	10.87
0.3		10.75	11.15
0.4		11.00	11.37
0.5		11.14	11.25

Note: $H$ = building height; $B$ = building width; $D$ = building depth; and $α$ = exposure factor.

Below, wind tunnel results are compared with ASCE 7-22, AIJ, and ISO (which is similar to KDS).

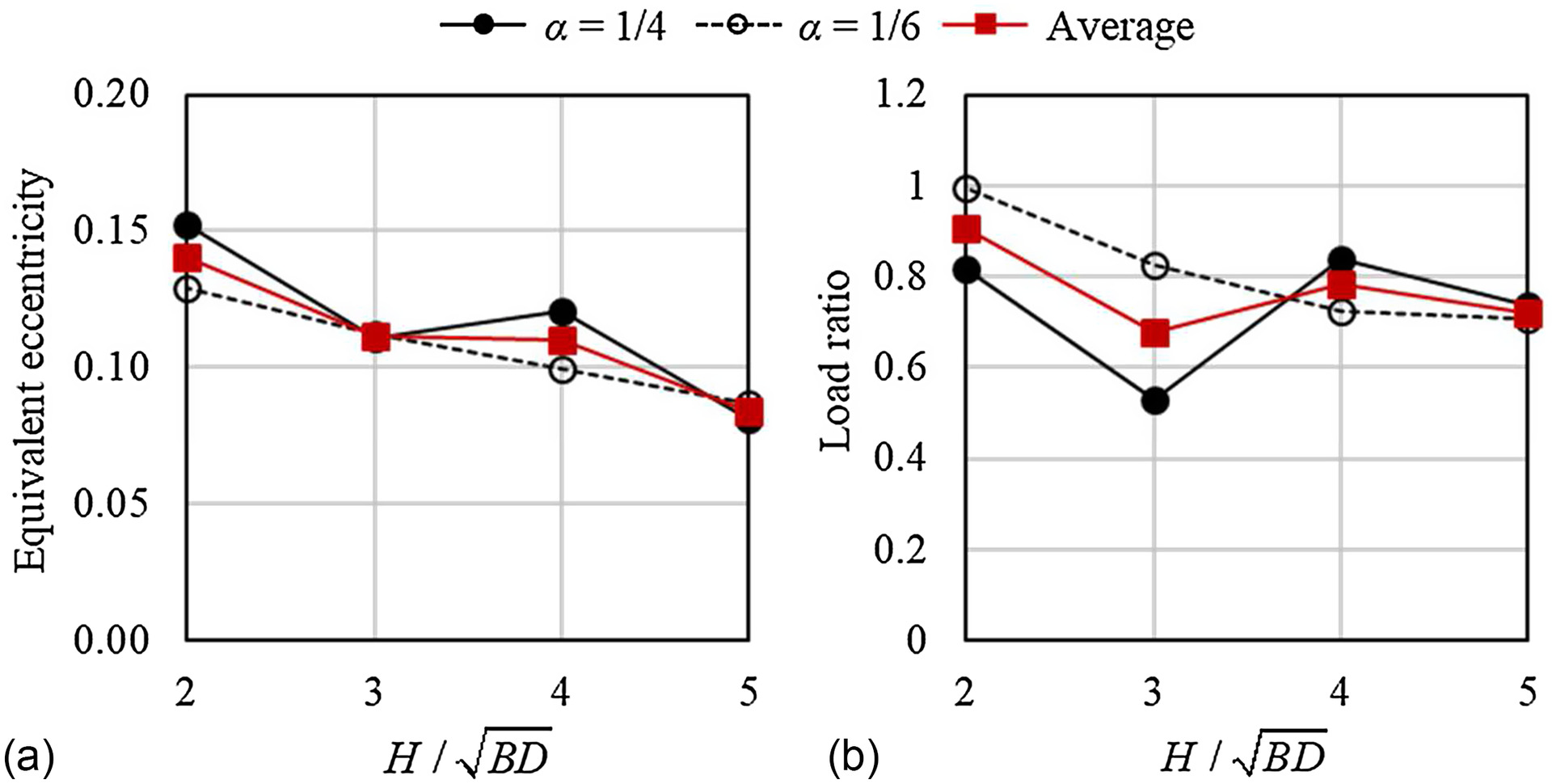
To compare the results based on wind tunnel tests with ASCE 7-22, equivalent eccentricity and load ratio were calculated for buildings with different aspect ratios and for angles of attack of 0°, as shown in Fig. 6. The results show that both equivalent eccentricity and load ratio decrease with increasing building aspect ratio. In general, the value of equivalent eccentricity for

α = 1 / 4

is considerably larger than that which can be attributed to the higher turbulence in comparison with

α = 1 / 6

, but the load ratio for

α = 1 / 4

is less than

α = 1 / 6

. Overall, the average value of equivalent eccentricity is between 0.1 and 0.15, which is comparable to the value of

e_{Q} = 0.15

in ASCE. For load ratio, the average value is between 0.7 and 0.9, which is generally compatible with the load ratio of 0.75 in ASCE.

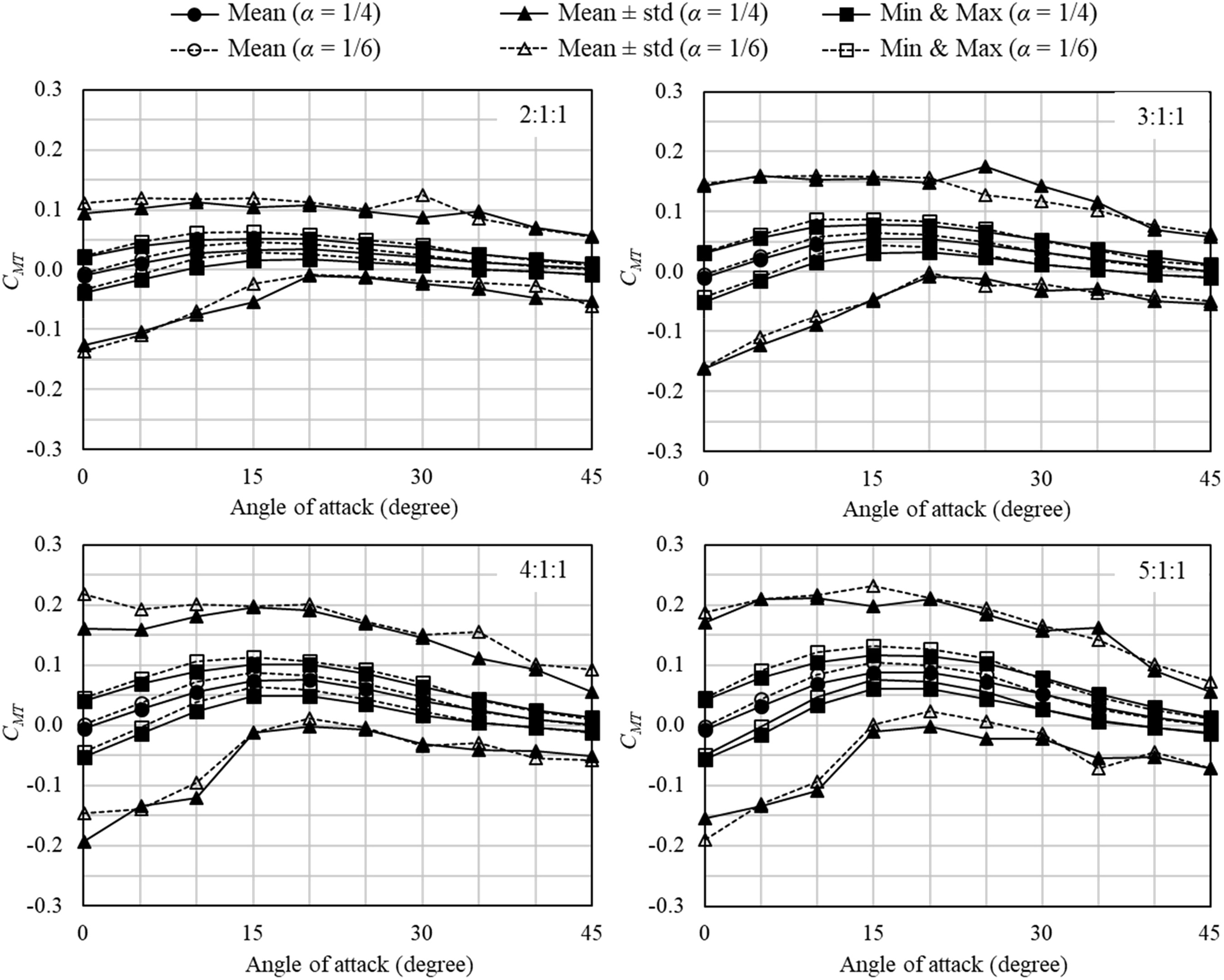
Fig. 6. (a) Equivalent eccentricity; and (b) load ratio based on TPU.

Normalized coefficient of base torsional moment,

C_{M T}

(obtained by dividing the component by

(q_{H} H B^{2})

), of buildings with different aspect ratio and exposure factor is shown in Fig. 7. According to the figure, the effect of exposure type is not considerable on the values of

C_{M T}

, especially for mean and standard deviation. In addition, the mean value is relatively small in comparison with standard deviation and maximum value, and is almost zero in the 0° angle of attack.

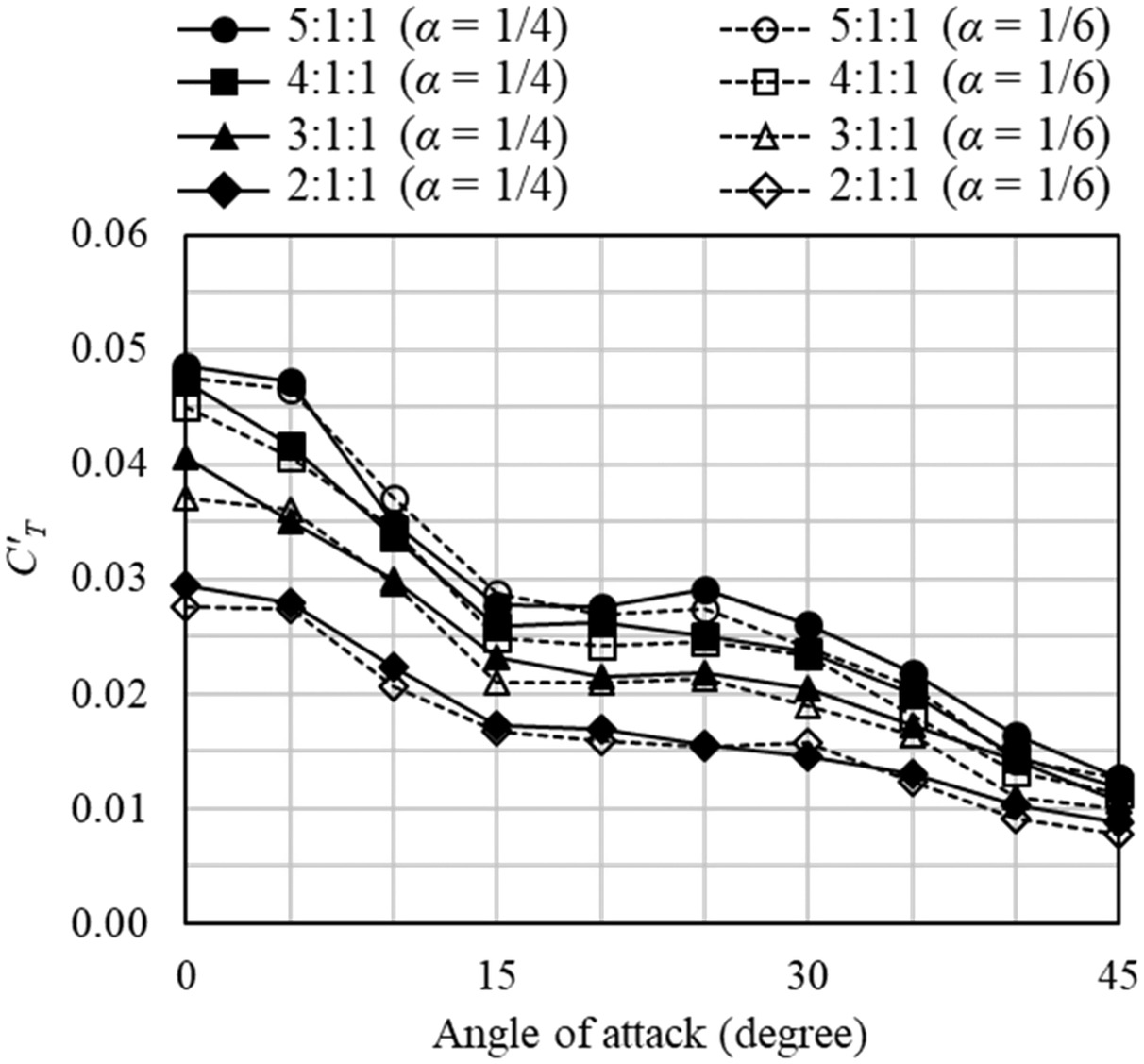
Fig. 7. Normalized coefficient of base torsional moment, $C_{M T}$ .

Fig. 8 shows the value of

C_{T}^{'}

[

= σ_{T B} / (q_{H} H B^{2})

] for the buildings to compare with the listed standards. It can be seen that the value of

C_{T}^{'}

for all buildings is maximum at the angle of attack of 0°, and its value decreases by increasing angle of attack. The effect of exposure type is also negligible.

Fig. 8. Normalized standard deviation of base torsional moment, $C_{T}^{'}$ .

The observations, including negligible value of the mean component and the largest value of

C_{T}^{'}

at an angle of attack of 0°, and recalling the fact that maximum along- and across-wind loads usually occur at the angle of attack of 0° for square-shape plan, confirm the consistency of the standards with the wind tunnel test results.

According to Fig. 8, the value of

C_{T}^{'}

at 0° angle of attack is between 0.03 and 0.05 for buildings with different aspect ratios, whereby increasing the aspect ratio, the difference between the values of

C_{T}^{'}

becomes smaller. Note that buildings with an aspect ratio of

2 ∶ 1 ∶ 1

are not in the covered range of the listed standards (Table 3). Based on test results, the values of

C_{T}^{'}

at 0° angle of attack for buildings with aspect ratios of

3 ∶ 1 ∶ 1

,

4 ∶ 1 ∶ 1

, and

5 ∶ 1 ∶ 1

are 0.037, 0.045, and 0.048, respectively.

The listed standards provide

C_{T}^{'}

as a function of plan aspect ratio (

D / B

) and independent of building aspect ratio. The value

C_{T}^{'}

for the building with

D / B = 1

, based on AIJ, is equal to 0.06 and, based on KDS and ISO, is equal to 0.05 (Table 7). Note that the value of ISO is multiplied by 0.6 (the mode shape correction) to be comparable with KDS and AIJ. The value from ISO almost fits with the value from wind tunnel tests for buildings with an aspect ratio of

5 ∶ 1 ∶ 1

, while the value from AIJ is about 20% larger.

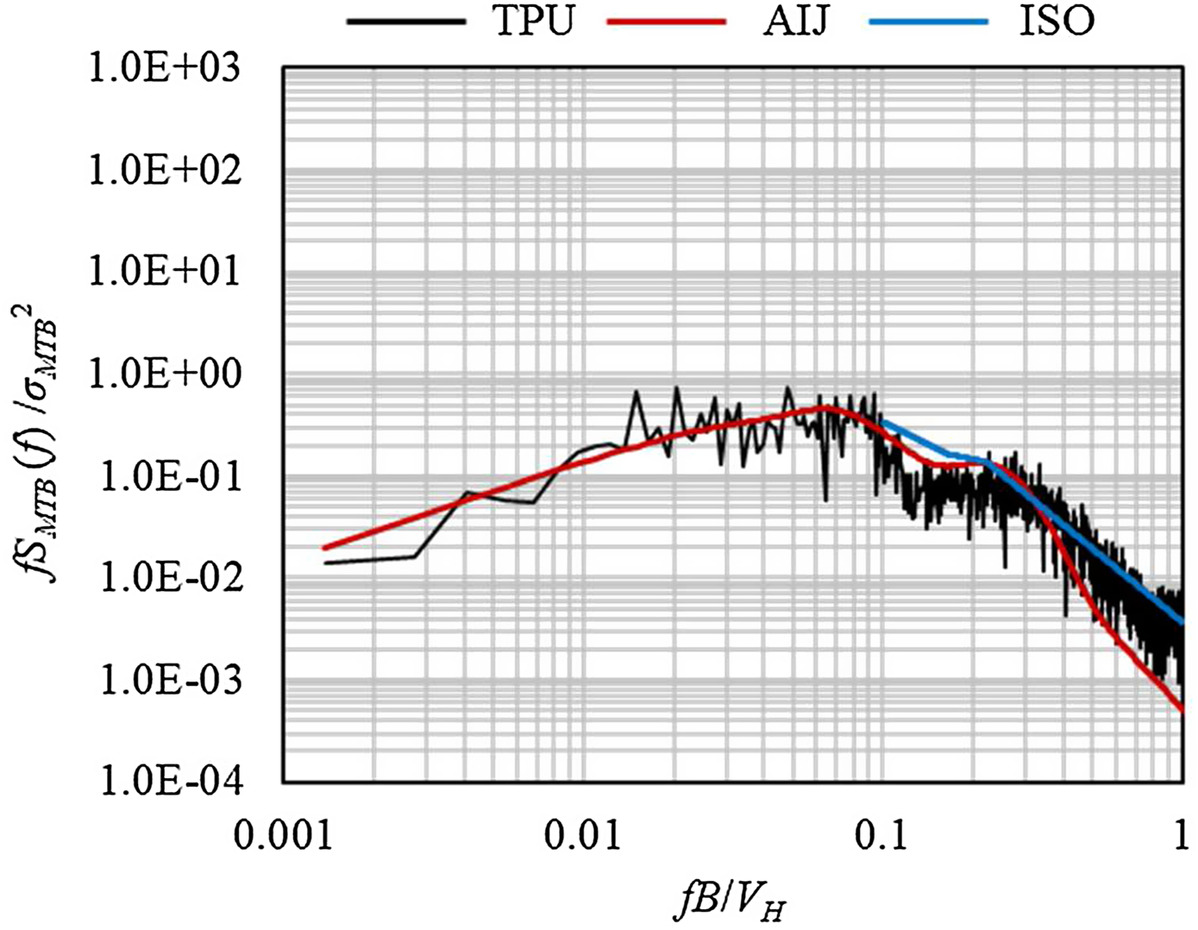
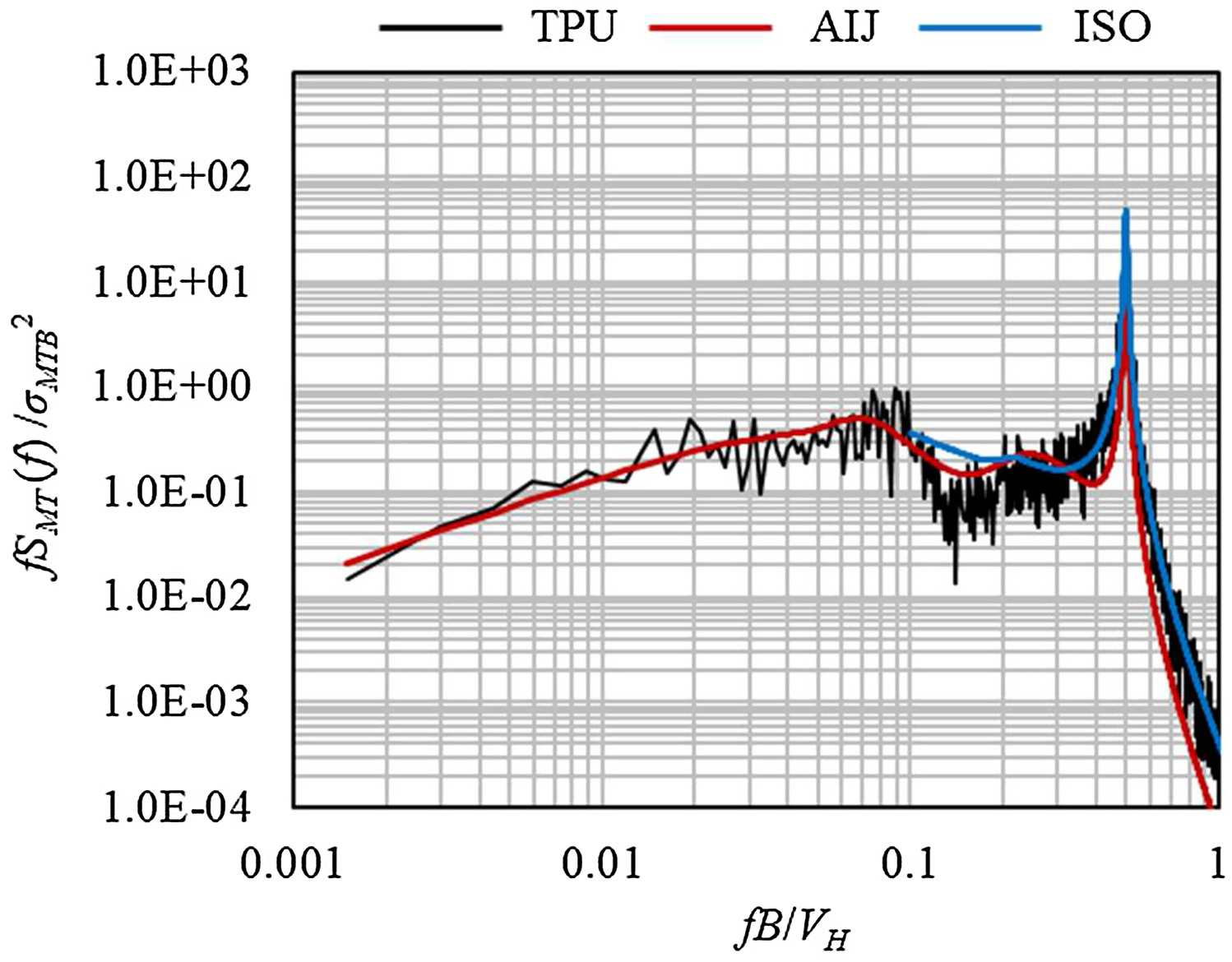
Normalized PSD of base torsional moment,

f S_{MTB} (f) / σ_{MTB}^{2}

, of buildings with an aspect ratio of

5 ∶ 1 ∶ 1

was calculated based on TPU results and compared with AIJ and ISO, as shown in Fig. 9. Note that the formulation in ISO does not cover the normalized frequency of less than 0.1. The results illustrate a good agreement between the standards and wind tunnel results. However, the model by AIJ can reproduce the step part of the PSD (in the range of normalized frequency between about 0.1 and 0.2) better than ISO. Although it is not depicted here, the results for other buildings show similar consistency.

Fig. 9. Normalized PSD of base torsional moment based on wind tunnel test, AIJ, and ISO ( $5 ∶ 1 ∶ 1$ and $α = 1 / 6$ ).

To compare equivalent static torsional-wind load, the first PSD of torsional response was calculated for buildings 200-m high, exposure C (

α = 1 / 6

), and angle of attack of 0°. Damping ratio,

ξ

, and wind speed at building height,

V_{H}

, were assumed to be equal to 1% and

45 m / s

, respectively. The response was calculated for normalized natural frequency of structure,

f_{T 1} B / V_{H}

, in the range of 0.1 to 0.5. Corresponding value of

f_{T 1}

was calculated and the PSD of torsional response based on wind tunnel results, AIJ, and ISO were obtained as the product of corresponding PSD and mechanical admittance function (Fig. 10). As shown in the figure, the PSD of the response based on the wind tunnel test results is in a good agreement with AIJ and ISO.

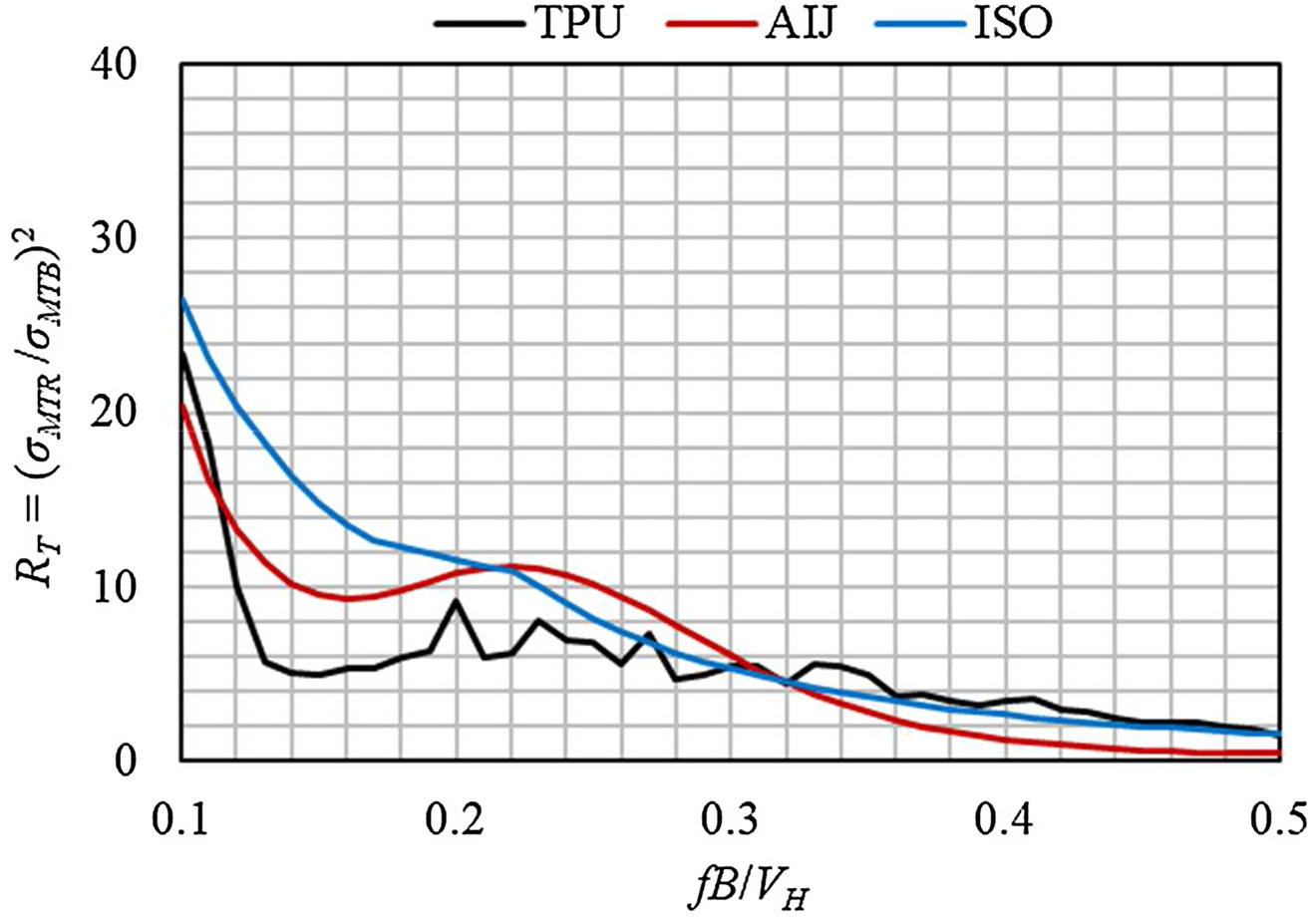
Fig. 10. Normalized PSD of torsional response based on wind tunnel test, AIJ, and ISO ( $5 ∶ 1 ∶ 1$ , $f_{T 1} B / V_{H} = 0.5$ , and $α = 1 / 6$ ).

In the next step, the standard deviation of the total response,

σ_{M T}

, was obtained by integration of the area below the PSD of the response. The standard deviation of resonant response,

σ_{MTR}

, was calculated by extracting background components,

σ_{MTB}

(which is equal to the standard deviation of the base torsional moment obtained from wind tunnel test) from the standard deviation of total response

(σ_{M T} = \sqrt{σ_{MTB}^{2} + σ_{MTR}^{2}})

. Then,

R_{T}

[

= {(σ_{MTR} / σ_{MTB})}^{2}

] was calculated and compared with the values of AIJ and ISO (refer to Tables 4–6), as shown in Fig. 11. It can be seen that the results from AIJ, ISO, and wind tunnel tests are comparable in most ranges. Values of

R_{T}

based on ISO for normalized frequency of 0.3 and larger match well with wind tunnel test results, and for normalized frequency less than 0.2 are more conservative than TPU. However, the results based on AIJ fit more closely with the trend based on wind tunnel test results, especially for normalized frequencies of 0.3 and less.

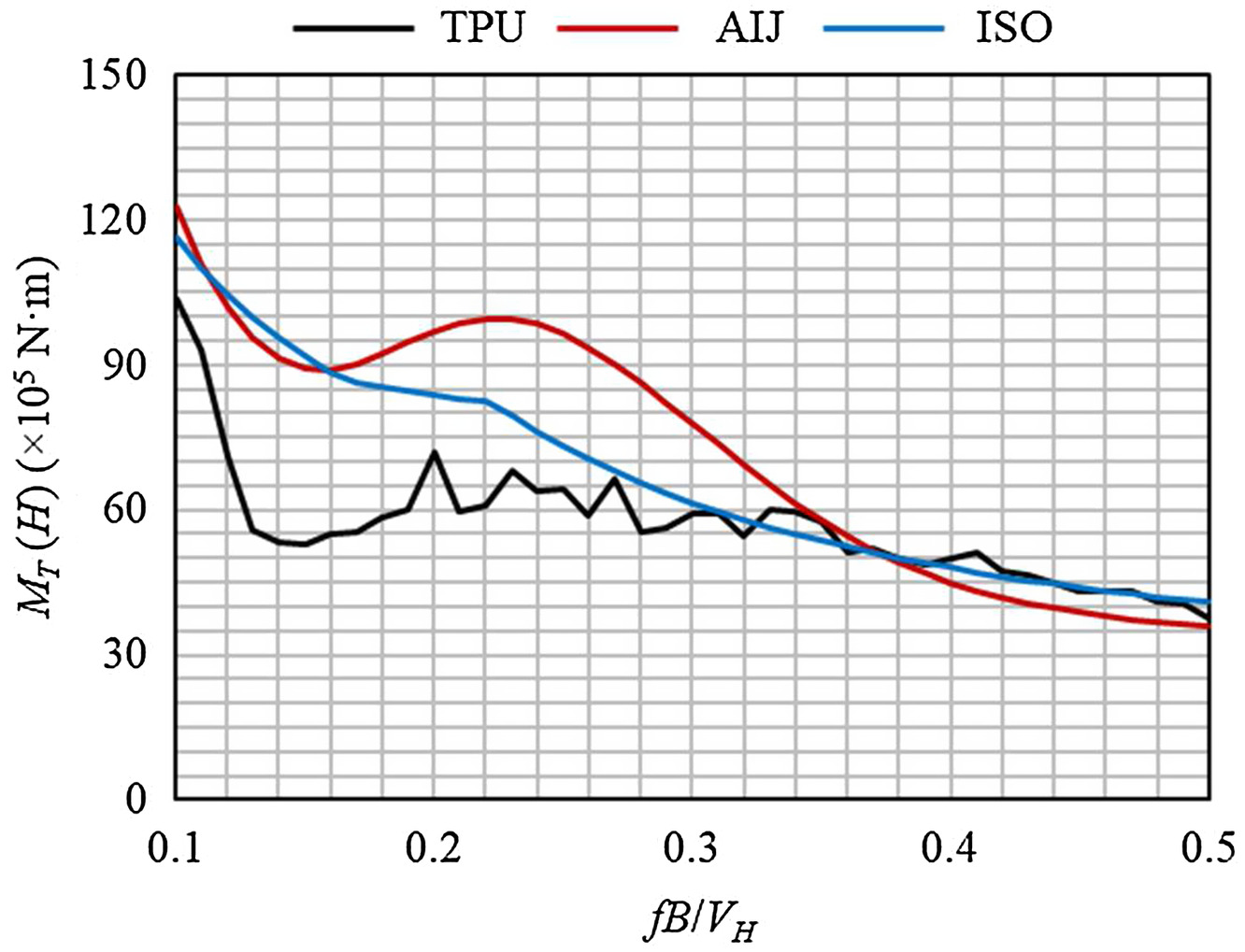
Fig. 11. Comparison of $R_{T}$ based on wind tunnel test, AIJ, and ISO ( $5 ∶ 1 ∶ 1$ and $α = 1 / 6$ ).

The equivalent static load is a function of both

C_{T}^{'}

and

R_{T}

. Therefore, the equivalent static torsional-wind load at building height,

M_{T}

(

H

), was calculated based on AIJ, ISO, and wind tunnel tests, as shown in Fig. 12.

M_{T}

(

H

) based on wind tunnel test results was calculated based on Eqs. (1) and (4), and

ϕ_{T 0} = 0.6

was used to be compatible with AIJ and ISO. Based on the results, for normalized frequencies of about 0.3 and larger, the load calculated from the wind tunnel test is comparable with AIJ and ISO. In addition, the values of AIJ and ISO are very close for normalized frequencies of less than about 0.2. The main reason for differences of AIJ and ISO for the range of 0.2 to 0.3 the different modeling for the step-shape part of the PSD. Overall, the value of both AIJ and ISO is larger than that based on the wind tunnel test for normalized frequencies of less than 0.3 (AIJ is between 20% and 70%, with an average of 50% larger, and ISO is between 2% and 80%, with an average of 34% larger). In addition to general conservatism in estimation of the load in comparison with wind tunnel test results, one reason can be that, based on AIJ, the provision is applicable to the structure with mass-stiffness eccentricity smaller than 0.15.

Fig. 12. Comparison of equivalent static torsional moment at building height, $M_{T}$ ( $H$ ), based on wind tunnel test, AIJ, and ISO ( $5 ∶ 1 ∶ 1$ and $α = 1 / 6$ ).

To evaluate the load case factors, a series of linear time-history analyses have been performed using a single degree of freedom (SDOF) system. For simplification, evaluation was done only for a building with an aspect ratio of

5 ∶ 1 ∶ 1

. Also, 0° angle of attack was chosen to be consistent with the listed standards. Properties of the SDOF system were defined using generalized mass and mass moment of inertia, stiffness, and damping with assumption of linear mode shape. Damping ratio,

ξ

, of 1% and 2% were examined as representative values for wind design.

Time-histories were made by dividing the full length of extracted data into five parts (with duration of 600 s in scaled-up time-histories), and ensemble averages were reported. To examine the results for different normalized frequencies (

f B / V_{H}

), two approaches can be taken: (1) fix

f

and change

V_{H}

, or (2) fix

V_{H}

and change

f

. With the change of

V_{H}

, time scale and length of time-histories vary. Because the correlation between the applied loads themselves is also important, particularly in higher values of normalized frequency where resonant components are small, it is crucial to avoid overlapping between the parts. For this reason,

V_{H}

was fixed to preserve the inherent correlation between the applied loads themselves. Recalling the values of length scale and duration of measurement, a value of

45 m / s

was chosen for

V_{H}

, at which the total time of five time series is almost equal to the total length of available data.

In addition to the values of natural frequencies, the studies by Somekawa et al. (2014) and Jeong and Kang (2021) showed that the ratio of frequencies is also important to calculate load case factors. They examined different cases of ratio of frequencies (in the range of 1 to 1.5), and found that if the frequencies are not equal (even for ratio of frequencies equal to 1.1), the load case factors can be significantly smaller than the case with equal frequencies. In contrast to ISO, the combination factors for directional load in AIJ are provided based on the frequency ratio (refer to Tables 9 and 10). SDOF systems were investigated with respect to natural frequencies, including natural frequency ratios of (

f_{D} ∶ f_{L} ∶ f_{T} = 1 ∶ 1 ∶ 1

) and (

f_{D} ∶ f_{L} ∶ f_{T} = 1 ∶ 1 ∶ 1.1

) as representative of cases with equal and nonequal frequencies.

Normalized frequencies were set in the range of 0.1 to 0.5 with an increment of 0.01, and for each value a set of five analyses for along-, across-, and torsional-wind directions were performed for two natural frequency ratios and two damping ratios. Because the values of

V_{H}

(

45 m / s

) and

B

(40 m) were constant, natural frequency was defined by manipulating corresponding normalized frequency and associated stiffness and damping coefficient of the SDOF system.

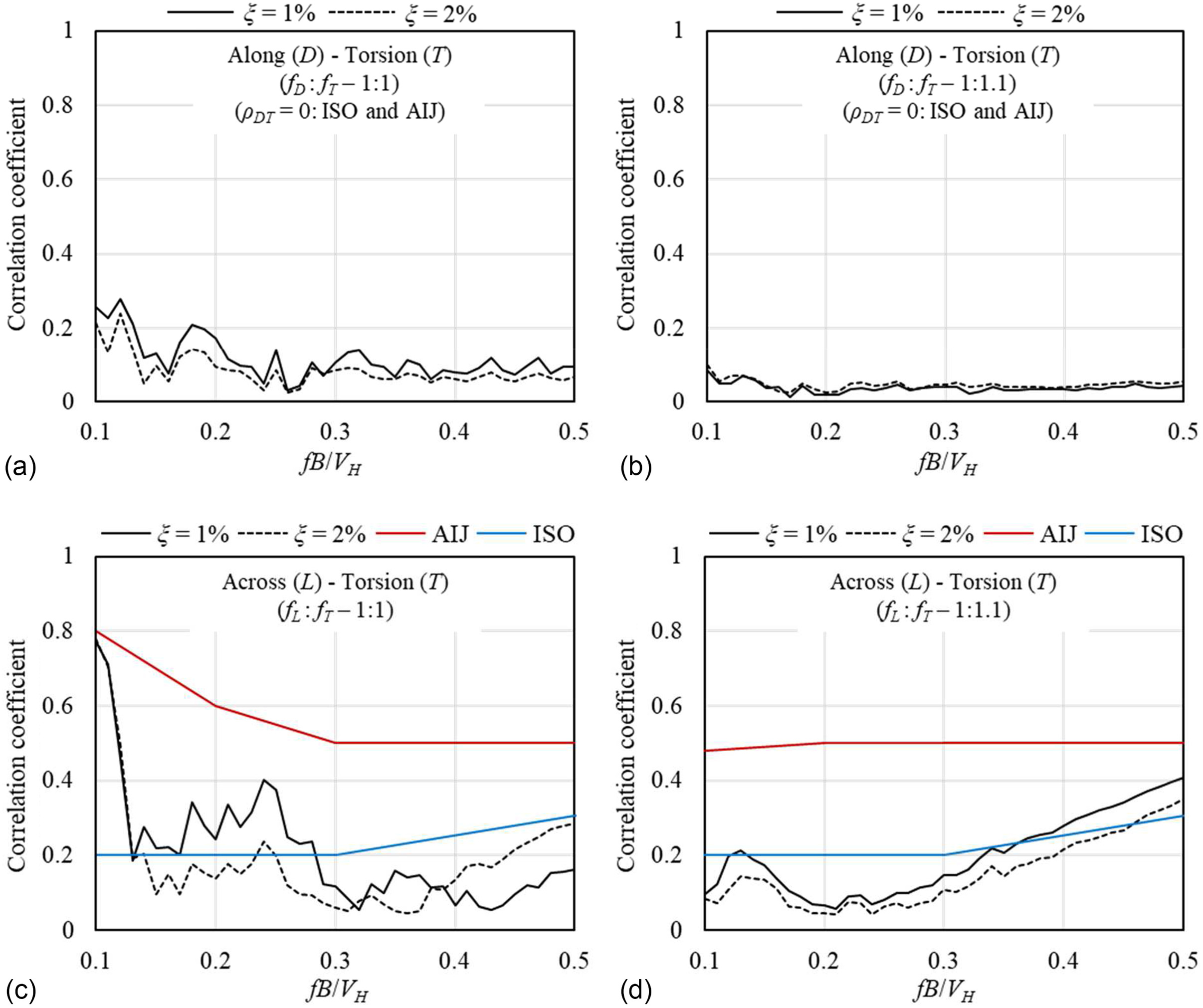
Absolute values of correlation coefficient between the fluctuation components of responses for along- and torsional-wind directions and across- and torsional-wind directions are shown in Fig. 13. It can be seen that the correlation coefficient between along- and torsional-wind responses,

ρ_{D T}

, is very small in all ranges of normalized frequencies and for both cases of (

f_{D} ∶ f_{T} = 1 ∶ 1

) and (

f_{D} ∶ f_{T} = 1 ∶ 1.1

). Therefore, it is logical to assume that along- and torsional-wind responses are uncorrelated.

Fig. 13. Correlation coefficient between responses: (a) ( $f_{D} ∶ f_{T} = 1 ∶ 1$ ); (b) ( $f_{D} ∶ f_{T} = 1 ∶ 1.1$ ); (c) ( $f_{L} ∶ f_{T} = 1 ∶ 1$ ); and (d) ( $f_{L} ∶ f_{T} = 1 ∶ 1.1$ ).

For the case of (

f_{L} ∶ f_{T} = 1 ∶ 1

), the correlation coefficient between across- and torsional-wind responses,

ρ_{L T}

, is very large at a small normalized frequency around 0.1, and decreases by increasing the normalized frequency. For the case of (

f_{L} ∶ f_{T} = 1 ∶ 1.1

), there is no large correlation at small normalized frequencies. At higher normalized frequency of about 0.3 or larger,

ρ_{L T}

increases for both cases of (

f_{L} ∶ f_{T} = 1 ∶ 1

) and (

f_{L} ∶ f_{T} = 1 ∶ 1.1

). Because the resonant component of responses is smaller at higher normalized frequency, large values of

ρ_{L T}

are due to the correlation between across- and torsional-wind loads itself rather than the responses. According to the results, the values provided by ISO are close to the average value of correlation coefficients in the examined range of normalized frequency, and the values provided by AIJ are based on an envelope to the analysis results with some degree of conservatism. For the case of (

f_{L} ∶ f_{T} = 1 ∶ 1

) at smaller values of normalized frequency, the correlation coefficients provided by AIJ fit better with the analysis results than those provided by ISO. For the case of (

f_{L} ∶ f_{T} = 1 ∶ 1.1

), large values of

ρ_{L T}

at small normalized frequency are not observed. These observations imply that, with a little difference between the natural frequencies, the correlation coefficient is very small for small normalized frequency.

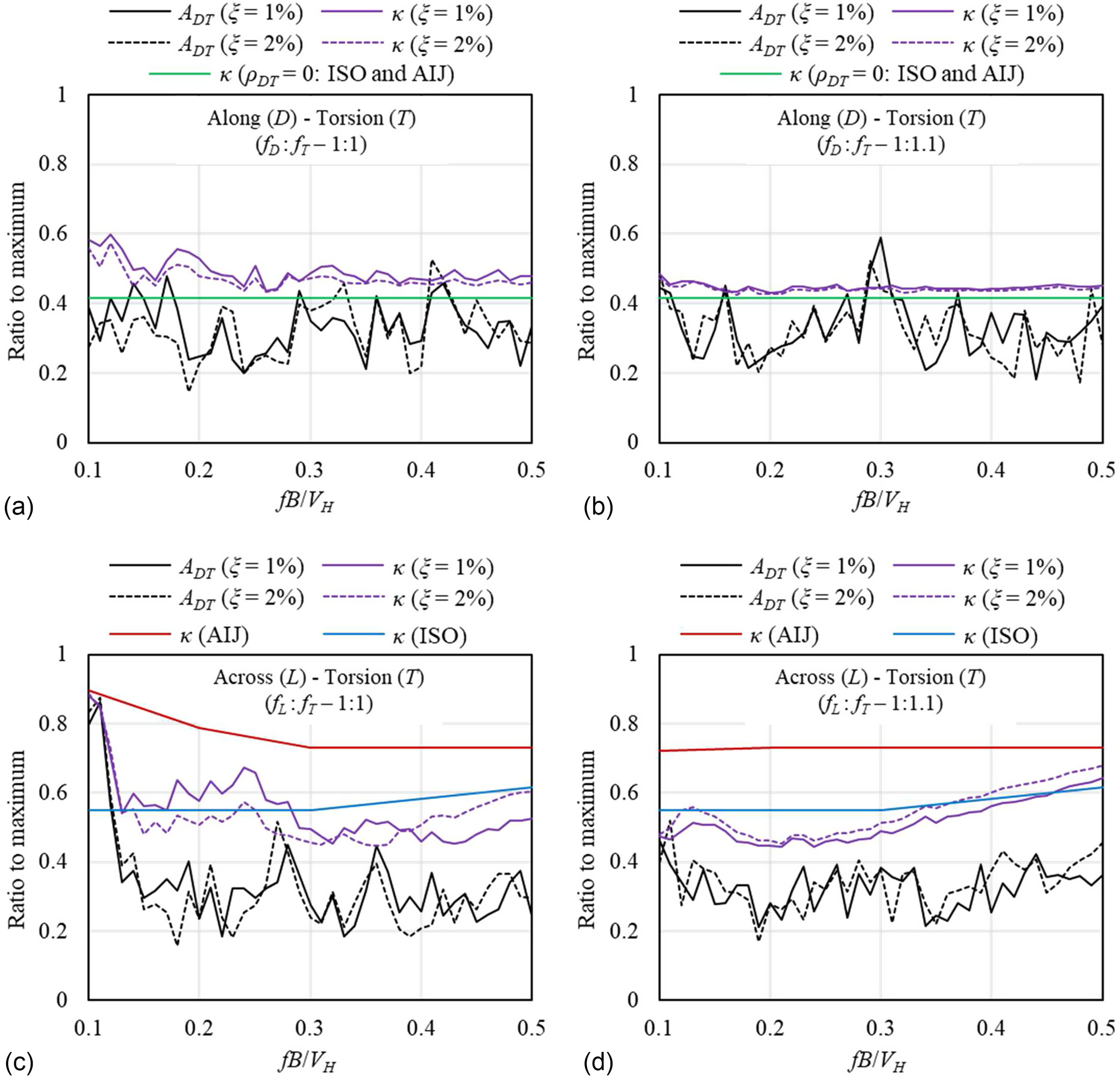
In the next step, the value of a component when the other component is the maximum was extracted from the results of time-history analysis, and scaled by the maximum value of that time-history (i.e.,

m_{Y X} / m_{Y \max}

). Ensemble average of these ratios was calculated for each set of five time-histories, and is denoted by

A_{Y X}

(ratio to the maximum). Here,

Y

and

X

are

D

for along-wind,

L

for across-wind, and

T

for torsional-wind (for instance,

A_{D T}

is equal to

m_{D T} / m_{D \max}

). It is worth mentioning that for every two components, two cases including

A_{X Y}

and

A_{Y X}

can be calculated, and the maximum of two is shown in Fig. 14. Additionally, values of

κ

based on correlation coefficients shown in Fig. 13, uncorrelated cases for along-wind and torsional-wind (

ρ_{D T} = 0

, similar to the assumption of ISO and AIJ), and the provided values of ISO and AIJ for across-wind and torsional-wind are calculated and shown in Fig. 14.

Fig. 14. Comparison of values of $A_{X Y}$ and $κ$ based on analysis and ISO: (a) ( $f_{D} ∶ f_{T} = 1 ∶ 1$ ); (b) ( $f_{D} ∶ f_{T} = 1 ∶ 1.1$ ); (c) ( $f_{L} ∶ f_{T} = 1 ∶ 1$ ); and (d) ( $f_{L} ∶ f_{T} = 1 ∶ 1.1$ ).

It can be seen that values of

κ

for the exact value of

ρ_{D T}

and for

ρ_{D T} = 0

are very close, especially for (

f_{D} ∶ f_{T} = 1 ∶ 1.1

). The values of

A_{D T}

and

κ

are well matched in all the ranges of normalized frequencies. Thus, the value of 0.4 for

κ

in AIJ and ISO, with the assumption that along-wind and torsional-wind responses are uncorrelated, seems logical.

As shown in Fig. 14, the value of

κ

based on wind tunnel tests is matched with that based on AIJ and ISO, except for the small normalized frequency around 0.1 where the underestimation by ISO is quite large. However, for the case with (

f_{L} ∶ f_{T} = 1 ∶ 1.1

), the accuracy is higher and the values are closer. It is worth mentioning that natural frequency of tall buildings in translational and torsional modes are usually different in practice, and thus the application of the case with (

f_{L} ∶ f_{T} = 1 ∶ 1

) is limited.

Summary and Conclusion

The purpose of the present study was to discuss perspectives behind the source of torsional-wind load and the current code-based procedures. Characteristics of torsional moment due to asymmetric wind pressure distribution on building surfaces (aerodynamic source) and possible torsional vibration in response to the load were explained, which are primary components of torsional-wind load. The role of mass-stiffness eccentricity in calculation of torsional load was clarified, and it was explained that the contribution of mass-stiffness eccentricity can be significant and should be carefully considered in the calculation of the load. Accordingly, it was noted that for even buildings with no inherent eccentricity between centers of mass and stiffness, a minimum eccentricity (accidental eccentricity) may need to be considered for more reliable design. The concept is similar to that commonly used in seismic design to address uncertainties in both dead and live loads, and quantitative research on this aspect is being conducted.

Although procedures in wind standards for calculating torsional-wind load from a theoretical point of view should be the same, clear differences can be seen in the formulation among various codes. To clarify these differences and perspectives, procedures in ASCE 7-22, AS/NZS 1170.2-2011, AIJ-RLB-2015, ISO 4354-2009, and KDS 41-2019 were explained in detail. In the next step, the main parameters of the standards were comprehensively compared with the results of wind tunnel test for several case studies. In general, a good consistency was observed between results of the standards and wind tunnel tests for the covered range of each standard.

It is expected that the study will lead to a deeper understanding of the critical parameters that should be considered in the calculation of torsional-wind load, which can result in a more logical and accurate design.

Notation

The following symbols are used in this paper:

$A$: projected area normal to wind direction;
$A_{Y X}$: ratio to the maximum ( $= m_{Y X} / m_{Y \max}$ );
$B$: width of building normal to wind direction;
$B_{X}$: width of building normal to $x$ -axis;
$B_{Y}$: width of building normal to $y$ -axis;
$C_{g}$: geometric center;
$C_{M T}$: normalized coefficient of base torsional moment;
$C_{m}$: mass center;
$C_{s}$: elastic stiffness center;
$C_{T}^{'}$: normalized standard deviation of base torsional moment [ $= σ_{MTB} / (q_{H} H B^{2})$ ];
$D$: width of building parallel to wind direction;
$e$: eccentricity for flexible buildings (ASCE 7-22);
$e_{D R}$: eccentricity between centers of mass and stiffness for along-wind load;
$e_{D S}$: eccentricity between centers of geometry and stiffness for along-wind load;
$e_{L R}$: eccentricity between centers of mass and stiffness for across-wind load;
$e_{L S}$: eccentricity between centers of geometry and stiffness for across-wind load;
$e_{Q}$: eccentricity for rigid buildings ( $= e_{s}$ ) (ASCE 7-22);
$e_{R}$: eccentricity between centers of mass and stiffness;
$e_{s}$: equivalent eccentricity for aerodynamic torsional-wind load [ $= M_{T S \max} / (F_{D S \max} B)]$ ;
$e_{X}$: eccentricity for flexible buildings for $x$ -axis (ASCE 7-22);
$e_{Y}$: eccentricity for flexible buildings for $y$ -axis (ASCE 7-22);
$F_{B}$: component of $F_{T}$ due to the approach flow and turbulence created by the building (AIJ);
$F_{D}$: along-wind load;
${\bar{F}}_{D}$: mean component of along-wind load;
$F_{D B}$: background component of along-wind load;
$F_{D R}$: resonant component of along-wind load;
$F_{D S}$: summation of mean and background components of along-wind load;
$F_{D S \max}$: max of $F_{D S}$ ;
$F_{L}$: across-wind load;
${\bar{F}}_{L}$: mean component of across-wind load;
$F_{L B}$: background component of across-wind load;
$F_{L R}$: resonant component of across-wind load;
$F_{L S}$: summation of mean and background components of across-wind load;
$F_{L S \max}$: max of $F_{L S}$ ;
$F_{T}$: coefficient of spectrum in torsional vibration (AIJ, ISO, and KDS);
$F_{V}$: component of $F_{T}$ due to vortex shedding (AIJ);
$F_{W}$: component of $F_{T}$ due to reattachment (AIJ);
$f$: frequency;
$f_{n}$: natural frequency;
$f_{m}^{*}$: normalized frequency for $F_{B}$ and $F_{W}$ ( $= f_{1 T} B / V_{H}$ ) (AIJ);
$f_{S}^{*}$: normalized frequency for $F_{V}$ (AIJ);
$f_{1 D}$ , $f_{D}$: natural frequency of the first lateral mode in along-wind direction;
$f_{1 L}$ , $f_{L}$: natural frequency of the first lateral mode in across-wind direction;
$f_{1 T}$ , $f_{T}$: natural frequency of the first torsional mode;
$G_{D}$: gust-effect factor (AIJ, KDS), mean dynamic response factor for $F_{D}$ (ISO);
$g_{Q}$: peak factor for background response of along-wind load (ASCE 7-22);
$g_{R}$: peak factor for resonant response of along-wind load (ASCE 7-22);
$g_{T}$: peak factor for torsional-wind load;
$H$: building height;
$h$: story height;
$I_{H}$: turbulence intensity at building height;
$I_{T}$: generalized mass of building for torsional vibration;
$I_{T 1}$: generalized mass of building for torsional vibration for linear mode shape;
$I_{\bar{z}}$: turbulence intensity at equivalent height ( $0.6 H$ ) (ASCE 7-22);
$K$: mode shape correction factor (ISO);
$K_{T}$: amplification factor for the torsional vibration spectrum (KDS, ISO);
$L_{D B}$: greater value of $D$ and $B$ (ISO, KDS);
$M_{T}$: torsional-wind load, summation of aerodynamic and dynamic torsional-wind moments (exception: summation of aerodynamic and eccentric torsional-wind moments in ASCE 7-22);
${\bar{M}}_{T}$: mean component of torsional-wind load;
$M_{T B}$: background component of torsional-wind load;
$M_{T R}$: resonant component of torsional-wind load;
$M_{T S}$: summation of mean and background components of torsional-wind load;
$M_{T S \max}$: maximum of $M_{T S}$ ;
$M_{T T}$: total torsional-wind load (including $M_{T}$ and moments due to eccentricity);
$m_{Y \max}$: maximum value of Y(t);
$m_{Y X}$: value of $Y (t)$ at the moment that $X (t)$ is maximum;
$n_{1}$: smaller of $f_{1 L}$ and $f_{1 T}$ (AIJ, ISO, KDS);
$Q$: background response factor for along-wind load (ASCE 7-22);
$q_{H}$: velocity pressure at building height;
$R$: resonant response factor for along-wind load (ASCE 7-22);
$R_{d}$: deformation response factor;
$R_{T}$: normalized standard deviation of resonant response for torsional vibration [ $= {(σ_{MTR} / σ_{MTB})}^{2}$ ] and [ $= π F_{T} / (4 ξ_{1 T})$ in AIJ, ISO, and KDS];
$S$: power spectral density (PSD);
$S_{M T}$: PSD of torsional response;
$S_{MTB}$: PSD of base torsional moment;
$V_{H}$: wind speed at building height;
$V_{T}^{*}$: normalized wind speed for torsional vibration [ $= V_{H} / (f_{1 T} \sqrt{B D})$ ] (ISO, KDS);
$v_{1}$ , $v_{2}$ , $v_{3}$: factors related to $F_{V}$ (AIJ);
$w_{1}$ , $w_{2}$ , $w_{3}$: factors related to $F_{W}$ (AIJ);
$z$: elevation;
$α$: exponent of power law for mean wind speed profile;
$β$: exponent of power law for mode shape;
$β_{T}$: exponential factor for the normalized wind speed for the torsional vibration (ISO, KDS);
$κ$: wind load combination factors for across- and torsional-wind loads (ISO, KDS);
$μ$: mode shape [ $= {(z / H)}^{β}$ ];
$ϕ$: phase angle;
$ϕ_{T}$: mode shape correction factor;
$ϕ_{T 0}$: mode shape correction factor for generalized base torsion;
$ρ$: correlation coefficient;
$ρ_{D L}$: correlation coefficient between along- and across-wind loads;
$ρ_{D T}$: correlation coefficient between along- and torsional-wind loads;
$ρ_{L T}$: correlation coefficient between across- and torsional-wind loads;
$σ$: standard deviation;
$σ_{M T}$: standard deviation of response;
$σ_{MTB}$: standard deviation of measured base torsional moment;
$σ_{MTR}$: standard deviation of resonant response;
$ξ$: damping ratio; and
$ξ_{1 T}$: damping ratio of the first torsional mode.

Appendix I. Procedure for Equivalent Static Torsional-Wind Load (AIJ, ISO, and KDS)

The general procedure to obtain equivalent static torsional-wind load based on peak rotation is as follows. The equivalent static torsional-wind load is defined as the product of peak factor for torsion,

g_{T}

, and standard deviation of the equivalent static load,

σ_{M T} (z)

, at the height

z

, that is,

M_{T} (z) = g_{T} σ_{M T} (z)

. It can be defined as

M_{T} (z) = K_{θ} (z) θ_{\max} (z)

, where

K_{θ} (z)

is torsional stiffness at height

z

; and

K_{θ} (z)

can be estimated as

I (z) {(2 π f_{1 T})}^{2}

, where

I (z)

is mass moment of inertia at height

z

, and

f_{1 T}

is the frequency of first torsional mode (Ha 2017). The peak rotation is defined by

θ_{\max} (z) = g_{T} σ_{θ^{*}} μ (z)

, where

σ_{θ^{*}}

is standard deviation of generalized rotation,

θ^{*}

, and

μ (z)

is the mode shape. Given the above, torsional-wind load can be defined by

M_{T} (z) = I (z) {(2 π f_{1 T})}^{2} g_{T} σ_{θ^{*}} μ (z)

(10)

Given the dynamic properties of the building,

σ_{θ^{*}}

are determined from postprocessing of the results from wind tunnel tests. The basic parameters from the test are standard deviation of background torsional moment at the base,

σ_{MTB}

, and its power spectral density (PSD),

S_{MTB} (f)

, where

f

is frequency. The generalized externally applied torsional-wind load,

M_{T B}^{*} (t)

, is defined by

M_{T B}^{*} (t) = \int_{0}^{H} M_{T B} (z, t) μ (z) d z

(11)

where

M_{T B} (z, t)

= external torsional moment at height

z

and time

t

. Assuming uniform mode shape, that is,

μ (z) = 1

,

M_{T B}^{*} (t)

and measured base torsion from the test are equal. Therefore, the PSD of

M_{T B}^{*} (t)

,

S_{{MTB}^{*}} (f)

, is equal to the PSD of base torsion,

S_{MTB} (f)

, and so the PSD of

θ^{*}

,

S_{θ^{*}} (f)

, can be defined by

S_{θ^{*}} (f) = \frac{S_{MTB} (f) {| H (f) |}^{2}}{K_{θ}^{* 2}}

(12)

where

{| H (f) |}^{2} = {({[1 - {(f / f_{1 T})}^{2}]}^{2} + {[2 ξ_{1 T} (f / f_{1 T})]}^{2})}^{- 1}

is the mechanical transfer function;

ξ_{1 T}

is the damping ratio in first torsional mode;

K_{θ}^{*} = I^{*} {(2 π f_{1 T})}^{2}

is the generalized torsional stiffness; and

I^{*} = \int_{0}^{H} I (z) μ^{2} (z) d z

is generalized mass moment of inertia. The value of

σ_{θ^{*}}

is obtained by integrating the PSD of torsional response,

σ_{θ^{*}} = \sqrt{\int_{0}^{\infty} S_{θ^{*}} (f) d f}

. Substituting

S_{θ^{*}} (f)

from Eq. (12) and calculation of the integral, and then decomposing

σ_{θ^{*}}

into resonant and background components,

σ_{θ^{*}}

can be expressed by

σ_{θ^{*}} = \frac{σ_{MTB}}{{(2 π f_{1 T})}^{2} I^{*}} \sqrt{1 + R_{T}}

(13)

where

R_{T}

= normalized standard deviation of resonant response. By substituting

σ_{θ^{*}}

from Eq. (13) into Eq. (10),

M_{T}

is defined by

M_{T} (z) = \frac{I (z)}{I^{*}} g_{T} σ_{MTB} μ (z) \sqrt{1 + R_{T}}

(14)

By assuming a linear mode shape and

I (z) = I

, the ratio of

I (z) / I^{*}

is equal to

3 / H

.

Where resonance response is measured as peak acceleration [

{\ddot{θ}}_{\max} (z)

], the general procedure is the same, and standard deviation of angular acceleration (

σ_{\ddot{θ}}

) can be estimated as

σ_{θ} / {(2 π f_{1 T})}^{2}

.

Appendix II. Derivation of Eccentricity for Flexible Building (ASCE)

Eq. (2) is obtained by modifying gust-effect factor in ASCE 7-22. Along-wind load in ASCE 7-22 is defined by

F_{D} = q_{3 s} C_{d} A G

(15)

where

q_{3 s}

= 3-second gust velocity pressure based on basic wind speed, which is 3-second gust wind speed;

A

= projected area normal to wind direction;

C_{d}

= drag force coefficient; and

G

= gust-effect factor, which is defined by

G = 0.925 \frac{1 + 1.7 I_{\bar{z}} \sqrt{{(g_{Q} Q)}^{2} + {(g_{R} R)}^{2}}}{1 + 1.7 g_{V} I_{\bar{z}} g_{V}}

(16)

A multiplier of 0.925 is included to match the value of

G

with its values in former versions of the code (Kwon and Kareem 2013; ASCE 1995). The numerator and denominator of Eq. (16) are gust-displacement factor,

G_{X}

, and gust-pressure factor,

G_{q}

, respectively.

In general, gust load factor (GLF) is defined by

G_{X}

, which is the ratio of peak displacement to mean displacement. Recalling the numerator of Eq. (16), the terms

1.7 I_{\bar{z}} g_{Q} Q

and

1.7 I_{\bar{z}} g_{R} R

are called background and resonant components of

G_{X}

, which are shown by

G_{X B}

and

G_{X R}

, respectively.

G_{X}

can be written as

G_{X} = 1 + \sqrt{G_{X B}^{2} + G_{X R}^{2}}

(17)

In ASCE 7-22, duration for averaging to obtain mean and peak wind speeds is 1 h and 3 s, respectively. However, rather than mean hourly wind speed, wind speed maps in ASCE 7-22 are based on gust wind speed (3-s average). As a result, the velocity pressure is also the peak value (gust velocity pressure), i.e.,

q_{3 s}

. Thus, it is reduced to mean hourly velocity pressure,

q_{1 h}

, by using

G_{q}

, which is the ratio of peak pressure to mean pressure (

q_{3 s} / q_{1 h}

). In this way,

G

in ASCE 7-22 is defined as the ratio of

G_{X} / G_{q}

to modify Eq. (17) as shown in Eq. (18) (Solari and Kareem 1998; Kwon and Kareem 2013)

F_{D} = q_{3 s} C_{d} A \frac{G_{X}}{G_{q}} = q_{1 h} C_{d} A G_{X}

(18)

This approach is used wherever peak (or gust) wind speed is provided instead of mean wind speed. A similar concept is also implemented in AS/NZS (2011) and the peak approach in ISO 4354 (ISO 2009). However, in standards such as AIJ (2015), KDS 41 (KDS 2019), the mean approach of ISO 4354 (ISO 2009), where basic wind speed is the mean value (10-min. mean wind speed), this modification is not included.

Mean (hourly) along-wind load,

{\bar{F}}_{D}

, can be obtained as the ratio of

F_{D} / G_{X}

. Eq. (18) can be rewritten as

F_{D} = {\bar{F}}_{D} + \sqrt{F_{D B}^{2} + F_{D R}^{2}}

(19)

where

F_{D B}

(

= {\bar{F}}_{D} G_{X B}

) and

F_{D R}

(

= {\bar{F}}_{D} G_{X R}

) are background and resonant components of along-wind load, respectively. Multiplying each component of along-wind load (mean, background, and resonant) by its corresponding eccentricity, corresponding component of torsional-wind load can be obtained. Recalling eccentricity for mean and background (

e_{Q}

) and eccentricity for resonant component (

e_{R}

), the mean, background, and resonant components of torsional-wind load are

e_{Q} B {\bar{F}}_{D}

;

e_{Q} B {\bar{F}}_{D} G_{X B}

; and

e_{R} B {\bar{F}}_{D} G_{X R}

, respectively. A modified form of gust-displacement factor for torsional-wind load,

G_{X}^{'}

, simply can be defined by

G_{X}^{'} = e_{Q} + 1.7 I_{\bar{z}} \sqrt{{(g_{Q} Q e_{Q})}^{2} + {(g_{R} R e_{R})}^{2}}

(20)

Finally,

e

is defined as the ratio of

G_{X}^{'} / G_{X}

for calculation of torsional-wind load directly based on calculated along-wind load, as shown in

M_{T} = e B F_{D} = \frac{G_{X}^{'}}{G_{X}} q_{1 h} C_{d} A B G_{X} = q_{1 h} C_{d} A B G_{X}^{'}

(21)

Data Availability Statement

All data, models, and code generated or used during the study appear in the published article.

Acknowledgments

This research was supported by National Research Foundation of Korea (No. 2021R1D1A1B06044752) and by the Institute of Construction and Environmental Engineering at Seoul National University. The views expressed are those of the authors, and do not necessarily represent those of the sponsors.

References

AIJ (Architectural Institute of Japan). 2004. Recommendations for loads on buildings. AIJ-RLB-2004. Tokyo: AIJ.

Google Scholar

AIJ (Architectural Institute of Japan). 2015. Recommendations for loads on buildings. AIJ-RLB-2015. Tokyo: AIJ.

Google Scholar

Alinejad, H., S. Y. Jeong, and T. H.-K. Kang. 2020. “Comparative assessment of ASCE 7-16 and KBC 2016 for determination of design wind loads for tall buildings.” Wind Struct. 31 (6): 575–591. https://doi.org/10.12989/was.2020.31.6.575.

Google Scholar

Alinejad, H., and T. H.-K. Kang. 2020a. “Engineering review of ASCE 7-16 wind-load provisions and wind effect on tall concrete-frame buildings.” J. Struct. Eng. 146 (6): 04020100. https://doi.org/10.1061/(ASCE)ST.1943-541X.0002622.

Google Scholar

Alinejad, H., and T. H.-K. Kang. 2020b. “Importance of considering accidental eccentricity in wind design of tall buildings.” In Proc., 2020 World Congress on Advances in Civil, Environmental, and Materials (ACEM20). Daejeon, South Korea: International Association of Structural Engineering and Mechanics.

Google Scholar

Asami, Y. 2000. “Combination method for wind loads on high-rise buildings.” [In Japanese.] In Proc., 16th National Symp. on Wind Engineering, 531–534. Tokyo: Japan Association for Wind Engineering.

Google Scholar

ASCE. 1995. Minimum design loads and associated criteria for buildings and other structures. ASCE 7-95. Reston, VA: ASCE.

Google Scholar

ASCE. 2021. Wind tunnel testing for buildings and other structures. ASCE 49-21. Reston, VA: ASCE.

Google Scholar

ASCE. 2022. Minimum design loads and associated criteria for buildings and other structures. ASCE 7-22. Reston, VA: ASCE.

Google Scholar

AS/NZS (Australian/New Zealand Standard). 2011. Structural design actions—Part 2: Wind actions. AS/NZS 1170.2-2011. Sydney, NSW, Australia: Standards Australia.

Google Scholar

Blessmann, J. 1992. “Neighbouring wind effects on two tall buildings.” J. Wind Eng. Ind. Aerodyn. 42 (1–3): 1041–1052. https://doi.org/10.1016/0167-6105(92)90111-M.

Google Scholar

Blessmann, J., and J. D. Riera. 1985. “Wind excitation of neighbouring tall buildings.” J. Wind Eng. Ind. Aerodyn. 18 (1): 91–103. https://doi.org/10.1016/0167-6105(85)90076-5.

Google Scholar

Boggs, D., and J. Dragovich. 2006. “The nature of wind loads and dynamic response.” ACI Spec. Publ. 240 (Oct): 15–44.

Google Scholar

Boggs, D., N. Hosoya, and L. Cochran. 2000. “Sources of torsional wind loading on tall buildings: Lessons from the wind tunnel.” In Proc., Structures Congress and Exposition, Advanced Technology in Structural Engineering, 1–8. Reston, VA: ASCE.

Google Scholar

Chen, X., and A. Kareem. 2005. “Coupled dynamic analysis and equivalent static wind loads on buildings with three-dimensional modes.” J. Struct. Eng. 131 (7): 1071–1082. https://doi.org/10.1061/(ASCE)0733-9445(2005)131:7(1071).

Google Scholar

Chopra, A. K. 2017. Dynamics of structures: Theory and applications to earthquake engineering. London: Pearson.

Google Scholar

Cui, W., and L. Caracoglia. 2018. “A fully-coupled generalized model for multi-directional wind loads on tall buildings: A development of the quasi-steady theory.” J. Fluids Struct. 78 (Apr): 52–68. https://doi.org/10.1016/j.jfluidstructs.2017.12.008.

Google Scholar

Elsharawy, M., T. Stathopoulos, and K. Galal. 2012. “Wind-induced torsional loads on low buildings.” J. Wind Eng. Ind. Aerodyn. 104–106 (May): 40–48. https://doi.org/10.1016/j.jweia.2012.03.011.

Google Scholar

Ha, Y.-C. 2017. “Evaluation of the across-wind load and response of high-rise buildings.” [In Korean.] In MIDAS expert column. Seongnam, Korea: MIDAS Information Technology.

Google Scholar

Ha, Y.-C., Y.-S. Kil, S.-K. Hwang, and D.-W. Kim. 2007. “Simplified formulas for estimating the across-wind induced response of rectangular tall buildings.” [In Korean.] J. Archit. Inst. Korea Struct. Constr. 23 (6): 39–48.

Google Scholar

Holmes, J. D. 1987. “Mode shape corrections for dynamic response to wind.” Eng. Struct. 9 (3): 210–212. https://doi.org/10.1016/0141-0296(87)90017-4.

Google Scholar

Hui, Y., Y. Tamura, and Q. Yang. 2017. “Analysis of interference effects on torsional moment between two high-rise buildings based on pressure and flow field measurement.” J. Wind Eng. Ind. Aerodyn. 164 (May): 54–68. https://doi.org/10.1016/j.jweia.2017.02.008.

Google Scholar

ISO. 2009. Wind actions on structures. ISO 4354. Geneva: ISO.

Google Scholar

Isyumov, N., and P. C. Case. 2000. “Wind-induced torsional loads and responses of buildings.” In Proc., Structures Congress, Advanced Techniques in Structural Engineering. Reston, VA: ASCE.

Google Scholar

Jeong, S. Y., and T. H.-K. Kang. 2021. “Correlation of directional wind loads on high-rise buildings with square-shaped plan.” In Proc., 2021 World Congress on Advances in Structural Engineering and Mechanics (ASEM21). Daejeon, South Korea: International Association of Structural Engineering and Mechanics.

Google Scholar

Kareem, A. 1985. “Lateral-torsional motion of tall buildings to wind loads.” J. Struct. Eng. 111 (11): 2479–2496. https://doi.org/10.1061/(ASCE)0733-9445(1985)111:11(2479).

Google Scholar

Katsumura, A., H. Kawai, H. Terazaki, Y. Tamura, and Y. Fugo. 2014. “Modeling of wind-induced torsional moment on tall buildings.” [In Japanese.] In Proc., 23th National Symp. on Wind Engineering, 421–426. Tokyo: Japan Association for Wind Engineering.

Google Scholar

KDS (Korean Design Standard). 2019. Korean design standard. KDS 41-2019. Seoul: KDS.

Google Scholar

Khanduri, A. C., T. Stathopoulos, and C. Bédard. 1998. “Wind-induced interference effects on buildings—A review of the state-of-the-art.” Eng. Struct. 20 (7): 617–630. https://doi.org/10.1016/S0141-0296(97)00066-7.

Google Scholar

Kijewski, T., and A. Kareem. 1998. “Dynamic wind effects: A comparative study of provisions in codes and standards with wind tunnel data.” Wind Struct. 1 (1): 77–109. https://doi.org/10.12989/was.1998.1.1.077.

Google Scholar

Kwon, D. K., and A. Kareem. 2013. “Comparative study of major international wind codes and standards for wind effects on tall buildings.” Eng. Struct. 51 (Jun): 23–35. https://doi.org/10.1016/j.engstruct.2013.01.008.

Google Scholar

Li, Y., J. W. Zhang, and Q. S. Li. 2014. “Experimental investigation of characteristics of torsional wind loads on rectangular tall buildings.” Struct. Eng. Mech. 49 (1): 129–145. https://doi.org/10.12989/sem.2014.49.1.129.

Google Scholar

Liang, S., Q. S. Li, S. Liu, L. Zhang, and M. Gu. 2004. “Torsional dynamic wind loads on rectangular tall buildings.” Eng. Struct. 26 (1): 129–137. https://doi.org/10.1016/j.engstruct.2003.09.004.

Google Scholar

Lin, Y. K. 1967. Probabilistic theory of structural dynamics, 366. New York: McGraw-Hill.

Google Scholar

Marukawa, H., T. Ohkuma, and Y. Momomura. 1992. “Across-wind and torsional acceleration of prismatic high rise buildings.” J. Wind Eng. Ind. Aerodyn. 42 (1–3): 1139–1150. https://doi.org/10.1016/0167-6105(92)90121-P.

Google Scholar

Ryu, H.-J., D.-H. Shin, and Y.-C. Ha. 2020. “Serviceability evaluation methods for high-rise structures considering wind direction.” Wind Struct. 30 (3): 275–288. https://doi.org/10.12989/was.2020.30.3.275.

Google Scholar

Saiful Islam, M., B. Ellingwood, and R. B. Corotis. 1992. “Wind-induced response of structurally asymmetric high-rise buildings.” J. Struct. Eng. 118 (1): 207–222. https://doi.org/10.1061/(ASCE)0733-9445(1992)118:1(207).

Google Scholar

Solari, G., and A. Kareem. 1998. “On the formulation of ASCE 7-95 gust effect factor.” J. Wind Eng. Ind. Aerodyn. 77–78 (Sep): 673–684. https://doi.org/10.1016/S0167-6105(98)00182-2.

Google Scholar

Solari, G., and L. C. Pagnini. 1999. “Gust buffeting and aeroelastic behaviour of poles and monotubular towers.” J. Fluids Struct. 13 (7–8): 877–905. https://doi.org/10.1006/jfls.1999.0240.

Google Scholar

Solari, G., T. A. Reinhold, and F. Livesey. 1998. “Investigation of wind actions and effects on the Leaning Tower of Pisa.” Wind Struct. 1 (1): 1–23. https://doi.org/10.12989/was.1998.1.1.001.

Google Scholar

Somekawa, D., H. Kawai, and H. Nishimura. 2014. “Experimental study on the correlation coefficient for combination of wind loads.” [In Japanese.] In Proc., Summaries of Technical Papers of Annual Meeting, AIJ, Structures I, 149–150. Tokyo: Architectural Institute of Japan.

Google Scholar

Tallin, A., and B. Ellingwood. 1984. “Serviceability limit states: Wind induced vibrations.” J. Struct. Eng. 110 (10): 2424–2437. https://doi.org/10.1061/(ASCE)0733-9445(1984)110:10(2424).

Google Scholar

Tallin, A., and B. Ellingwood. 1985a. “Analysis of torsional moments on tall buildings.” J. Wind Eng. Ind. Aerodyn. 18 (2): 191–195. https://doi.org/10.1016/0167-6105(85)90097-2.

Google Scholar

Tallin, A., and B. Ellingwood. 1985b. “Wind-induced motion of tall buildings.” Eng. Struct. 7 (4): 245–252. https://doi.org/10.1016/0141-0296(85)90004-5.

Google Scholar

Tamura, Y. 2012. “Aerodynamic database for high-rise buildings.” In Tokyo: Global center of excellence program. Tokyo: Tokyo Polytechnic Univ.

Google Scholar

Tamura, Y., H. Kawai, Y. Uematsu, H. Marukawa, K. Fujii, and Y. Taniike. 1996. “Wind load and wind-induced response estimations in the recommendations for loads on buildings, AIJ 1993.” Eng. Struct. 18 (6): 399–411. https://doi.org/10.1016/0141-0296(95)00121-2.

Google Scholar

Tamura, Y., H. Kikuchi, N. Pillai, and K. Hibi. 2008. “Pressure distributions and flow fields imposing extreme wind force components.” In Proc., Int. Colloquium on Bluff Body Aerodynamics and Applications (BBAA VI), 20–24. Amsterdam, Netherlands: Elsevier.

Google Scholar

Yu, X. F., Z. N. Xie, X. Wang, and B. Cai. 2016. “Interference effects between two high-rise buildings on wind-induced torsion.” J. Wind Eng. Ind. Aerodyn. 159 (Dec): 123–133. https://doi.org/10.1016/j.jweia.2016.10.011.

Google Scholar

Zhang, W. J., Y. L. Xu, and K. C. S. Kwok. 1995. “Interference effects on aeroelastic torsional response of structurally asymmetric tall buildings.” J. Wind Eng. Ind. Aerodyn. 57 (1): 41–61. https://doi.org/10.1016/0167-6105(94)00098-X.

Google Scholar

Zhou, Y., and A. Kareem. 2000. “Torsional load effects on buildings under wind.” In Proc., Structures Congress, Advanced Techniques in Structural Engineering, 1–8. Reston, VA: ASCE.

Google Scholar

Zhou, Y., A. Kareem, and M. Gu. 2002. “Mode shape corrections for wind load effects.” J. Eng. Mech. 128 (1): 15–23. https://doi.org/10.1061/(ASCE)0733-9399(2002)128:1(15).

Google Scholar

Information & Authors

Information

Published In

Journal of Structural Engineering

Volume 149 • Issue 11 • November 2023

Copyright

This work is made available under the terms of the Creative Commons Attribution 4.0 International license, https://creativecommons.org/licenses/by/4.0/.

History

Published online: Sep 12, 2023

Published in print: Nov 1, 2023

Discussion open until: Feb 12, 2024

Authors

Affiliations

Hamidreza Alinejad https://orcid.org/0000-0002-4616-2131 [email protected]

Postdoctoral Researcher, Institute of Engineering Research, Seoul National Univ., 1 Gwanak-ro, Gwanak-gu, Seoul 08826, Korea. ORCID: https://orcid.org/0000-0002-4616-2131. Email: [email protected]

View all articles by this author

Thomas H.-K. Kang, M.ASCE [email protected]

Professor, Dept. of Architecture and Architectural Engineering and Institute of Engineering Research, Seoul National Univ., 1 Gwanak-ro, Gwanak-gu, Seoul 08826, Korea (corresponding author). Email: [email protected]

View all articles by this author

Seung Yong Jeong [email protected]

Postdoctoral Researcher, Institute of Engineering Research, Seoul National Univ., 1 Gwanak-ro, Gwanak-gu, Seoul 08826, Korea. Email: [email protected]

View all articles by this author

Byeonguk Ahn [email protected]

Ph.D. Student, Dept. of Architecture and Architectural Engineering, Seoul National Univ., 1 Gwanak-ro, Gwanak-gu, Seoul 08826, Korea. Email: [email protected]

View all articles by this author

Metrics & Citations

Metrics

Citations

Download citation

If you have the appropriate software installed, you can download article citation data to the citation manager of your choice. Simply select your manager software from the list below and click Download.

Engineering Review of Wind-Induced Torsional Moment and Response of Buildings

Abstract

Introduction

Aerodynamic Load Effect

Dynamic Response Effect and Role of Mass-Stiffness Eccentricity

Evaluation of Torsional-Wind Load by Wind Tunnel Tests

Exploring Torsional-Wind Load in Standards

Procedure in ASCE 7-22 and AS/NZS

Procedure in AIJ, ISO, and KDS

Comparison with Results of Wind Tunnel Tests

Summary and Conclusion

Notation

Appendix I. Procedure for Equivalent Static Torsional-Wind Load (AIJ, ISO, and KDS)

Appendix II. Derivation of Eccentricity for Flexible Building (ASCE)

Data Availability Statement

Acknowledgments

References

Information & Authors

Information

Published In

Copyright

History

Authors

Affiliations

Metrics & Citations

Metrics

Citations

Download citation

View Options

Media

Figures

Other

Tables

NEXT ARTICLE

Verify Phone

Congrats!

Abstract

Introduction

Aerodynamic Load Effect

Dynamic Response Effect and Role of Mass-Stiffness Eccentricity

Evaluation of Torsional-Wind Load by Wind Tunnel Tests

Exploring Torsional-Wind Load in Standards

Procedure in ASCE 7-22 and AS/NZS

Procedure in AIJ, ISO, and KDS

Comparison with Results of Wind Tunnel Tests

Summary and Conclusion

Notation

Appendix I. Procedure for Equivalent Static Torsional-Wind Load (AIJ, ISO, and KDS)

Appendix II. Derivation of Eccentricity for Flexible Building (ASCE)

Data Availability Statement

Acknowledgments

References

Information

Published In

Copyright

History

Authors

Affiliations

Metrics

Citations

Download citation

Figures

Other

Share

Copy the content Link

Share with email

Share

Request Username

Create a new account

Change Password

Password Changed Successfully

Verify Phone

Congrats!