Application of a Workflow to Determine the Feasibility of Using Simulated Streamflow for Estimation of Streamflow Frequency Statistics
Publication: Journal of Hydrologic Engineering
Volume 29, Issue 5
Abstract
Streamflow records from hydrologic models are attractive for use in operational hydrology, such as a streamflow frequency analysis. The amount of bias inherent to simulated streamflow from hydrologic models is often unknown, but it is likely present in derivative products. Therefore, a workflow may help determine where streamflow frequency analysis is credibly feasible from simulated streamflow and allow for a systematic way to assess and correct for bias. The proposed workflow consists of hydrologically matching model output locations with streamflow-gauging station (stream gauge) locations, computing the desired statistic from the simulated and observed streamflow record, computing the differences between the simulated and observed statistic (i.e., the bias), and constructing generalized additive models (GAMs) from the differences to determine bias corrections. The US Geological Survey, in cooperation with the Gulf Coast Ecosystem Restoration Council and the US Environmental Protection Agency, is testing the proposed workflow on a low-streamflow frequency (LFF) analysis. Simulated streamflows for the LFF analysis were sourced from a machine-learning model that estimated daily streamflow at Level-12 hydrologic unit code (HUC12) pour points (outlets) in the southern and southeastern US for 1950–2010. The comparison data set consists of 497 stream gauges that are coincident with a HUC12 outlet. The simulated LFF statistics were being overestimated on average; thus, there are limits to using simulated streamflow for frequency analysis. The magnitude of the overprediction generally increases where no-flow conditions are common. Bias corrections determined from the GAMs decreased the magnitude of bias observed in the simulated LFF statistics on average, suggesting it is feasible to expand the operational use of simulated streamflows to frequency analyses with the proposed workflow. The proposed workflow could be advantageous to practitioners interested in leveraging existing and future simulated streamflow data sets with regional and or global coverage.
Practical Applications
Globally, the direct observations of streamflow needed to characterize the likelihood of a hydrologic event (such as a flood or drought) are not readily available, and hydrologic models that predict streamflow at ungauged locations can ostensibly solve this problem. However, assumptions used to create these models could affect the accuracy of the results from streamflow analyses conducted with the modeled data. To address this issue, a workflow is proposed to assess and correct for any biases. The workflow involves matching the model output locations with streamflow-gauging station locations where there are direct observations, computing the desired streamflow statistic from the modeled and observed streamflow records, calculating the differences between them, and constructing models to determine correction values. The proposed workflow was tested on modeled streamflow data from the southern and southeastern US, and the results showed that there is some potential in using the predicted streamflow to solve operational problems like the statistical characterization of drought events.
Introduction
Hydrologic models are becoming more prevalent with advances in artificial intelligence and machine-learning methods (Kim et al. 2021). Accordingly, the employment of hydrologic model outputs to solve operational problems is likely to expand. In particular, simulated streamflow as a hydrologic model output has the potential to provide practitioners with the valuable data that are otherwise nonexistent and are needed for operational hydrology. However, with an increasing prevalence of diverse, often complex, hydrologic modeling approaches (Horton et al. 2022), multiple ways of assessing model performance (Ritter and Muñoz-Carpena 2013; Bourdin et al. 2012), and a timely need for decision-support products to have readily incorporated the latest climate-change science (Wasko et al. 2021; Blum et al. 2019), a practitioner who is far-removed from the modeling exercise risks employing simulated streamflow for an objective that is beyond the hydrologic model’s theoretical capabilities or one for which it is not uniquely calibrated (Zhang et al. 2018). The risk is inherent to scenarios involving the deterministic use of simulated streamflow from hydrologic models because the predictions do not possess the full distributional range and properties originally present in the observed streamflow (Farmer and Vogel 2016).
In operational hydrology, water-resource managers commonly require a statistical characterization of a hydrologic extreme, such as the probability or risk of a flood or drought. Practitioners generally conduct streamflow frequency analyses wherein observed streamflows are used to compute streamflow (flow) frequency statistics that the water-resource managers can use to make informed management decisions (Smakhtin 2001). There is increasing uncertainty in flow frequency statistics as the probability (depth into the tail of the flow frequency distribution) increases because of the extrapolation beyond available data, and this increasing uncertainty applies to frequency analyses based on observed and simulated streamflows alike. The problem is exacerbated if simulated streamflow outputs are used for left or right tail frequency estimates because of variance reduction (Kirby 1975; Vogel 1999; Farmer and Vogel 2016). Because many hydrologic models are data-driven, less available input for characterizing the left and right tails of the streamflow distribution means that models cannot be expected to reliably extrapolate extremes (Sivakumar 2005).
There are several states in the southern and southeastern US where the use of simulated streamflows for operational hydrology could be beneficial to water-resource managers. For example, estimates for low-flow frequency (LFF) statistics at gauged sites have been published by the USGS for the state of Mississippi (albeit not since the early 1990s) (Telis 1991), but there are no published estimates for ungauged locations. In contrast, there are at least four models to date that have simulated streamflow for ungauged locations in Mississippi. These data could be used to estimate LFF statistics at ungauged locations; however, a plot of the observed flow-duration curve (FDC) (gray line) (Searcy 1959) in Fig. 1 for a particular streamflow-gauging station (stream gauge) located in central Mississippi shows that the four hydrologic models (Russell et al. 2021; Robinson et al. 2020) misrepresent both the lower and upper tails of the streamflow distribution.
It is reasonable to assume that derivative products of the simulated streamflow, such as LFF statistics, would mimic the overestimation or underestimation, i.e., the bias, shown by the simulated streamflow examples at ungauged locations. Additionally, one could predict that the magnitude of the bias would increase as the depth into the tail of a probability distribution increases because the agreement with the observed FDC tends to decrease as tail depth increases in Fig. 1 (moving away from the middle of the plot).
Unlike the example in Fig. 1, where a model output location is coincident with a stream gauge, the direction and magnitude of the bias in the simulated streamflow at ungauged locations is unknown; therefore, assessing and correcting for the bias may be useful for practitioners interested in leveraging the growing wealth of hydrologic models for frequency work. Previous studies have compared the relative performance of simulated streamflow from different modeling approaches in context of a specific operational objective (Murphy et al. 2013; Guo et al. 2014; Zhang et al. 2018), but comparisons between models may cause practitioners to rely on a vetted model that will inevitably become outdated as new inputs become available or approaches improve. Others have investigated a general method for correcting the distributional bias of simulated streamflow outputs (Farmer et al. 2018), but a practitioner may need to know how the bias extends into the domain of an estimate derived from simulated streamflow. A more generalized bias assessment and correction workflow could be applied to any streamflow-frequency statistic derived from any simulated streamflow data set.
Objectives
The primary goal of this work is to provide practitioners with a general workflow to assess the feasibility of flow-frequency analyses from simulated streamflow data sets. In order to illustrate the application of the proposed workflow, the simulated streamflow data set from Robinson et al. (2020) is used to compute LFF statistics and associated bias assessment, bias correction, and uncertainty analysis, but it is intended to be flexible for use with simulated streamflow outputs from other hydrologic models, both past and future, and application to other types of flow-frequency analyses not tested here.
Scope
The proposed workflow consists of hydrologically matching model output locations with stream gauging locations, computing the desired flow-frequency statistic from the simulated and observational streamflow record, computing the differences between the simulated and observed flow-frequency statistic (i.e., the bias), modeling the differences to determine bias corrections, and propagating the uncertainties into the domain of the derivative statistic. Modeling the differences is essentially an exercise of modeling the residuals left over from the model used to simulate streamflow in the domain of each simulated flow-frequency statistic.
For a demonstration of the workflow, we used simulated streamflows provided by Robinson et al. (2020) for the period 1950–2009 that used the machine-learning model output from Worland et al. (2019a) at 9,203 Level-12 hydrologic unit code (HUC12) pour points (watershed outlet locations) for streams draining to the Gulf Coast (Fig. 2). The Robinson et al. (2020) data set has a large temporal range (six decades of streamflow represented), and the spatial coverage is large enough to investigate the characteristics of a spatial bias. Worland et al. (2019b, their Fig. 5) showed a combination of a statistical and a machine-learning approach is effective for modeling daily streamflow, with coverage probabilities that achieve near 95% for most nonexceedance probabilities not too deep in the tails. However, it is in the tails of the flow-frequency distribution where we (and practitioners, generally) have interest in the feasibility of operational use of simulated streamflow.
A comparison data set of 497 stream gauge-model pairs (Fig. 2) is used to explore the amount of bias shown by the simulated LFF statistics. Bias corrections are determined in a two-stage process by fitting thin-plate cross-validated splines to the stream gauge-model LFF statistic differences using generalized additive models (GAMs) (Wood 2003, 2011). The bias corrections are applied to the simulated LFF statistics to arrive at bias-corrected statistics, but more importantly, they are used to determine if the results are reliable or not in the specific context that a practitioner wishes to employ them in.
A LFF analysis was specifically chosen (as opposed to high flow) to test the workflow because the low-flow regime is inherently difficult to model. The low-flow regime is affected by various anthropogenic impacts such as groundwater abstraction (Smakhtin 2001) that are difficult to capture in data-driven hydrologic model input and calibration data sets. Consequently, the low-flow regime has greater variability in the predictions (Fig. 1) and promotes a better understanding of the feasibility of computing simulated statistics from an operational standpoint because large biases are to be expected.
LFF statistics are hereafter referred to with the notation format NQT for the averaging period, where N refers to day and Q is for flow at the T-year return period (7Q10, for example). Three N-day averaging periods (1, 7, and 30 days) and four return periods (2, 5, 10, and 20 years, the 0.50, 0.20, 0.10, and 0.05 nonexceedance probabilities, respectively) are investigated in this study for a total of 12 LFF statistics (1Q2, 1Q5, 1Q10, 1Q20, 7Q2, 7Q5, 7Q10, 7Q20, 30Q2, 30Q5, 30Q10, and 30Q20) to explore the effect of the N-day averaging period and depth into the tail on the bias.
The approach used for estimation of the magnitude of the LFF statistics follows conventional USGS frequency analyses for gauged locations in the study area (Funkhouser et al. 2008; Hammett 1985; Gotvald 2016; Martin and Arihood 2010; Telis 1991; Southard 2013; Huntzinger 1978; Law et al. 2009). Annual minima are computed for the climate years ranging from 1951 to 2009. The climate year is defined as April 1–March 31, where the climate year is the calendar year in which the period ends, thus covering the period from April 1, 1950, to March 31, 2009. Annual minima are fit to the three-parameter log-Pearson type III probability distribution (PE3) by method of L-moments (linear moments). Uncertainty of the magnitude of LFF is documented through 95% prediction limits.
Background
Low-Streamflow Frequency Analyses
Water-resources managers and planners are interested in LFF statistics to assess effluent discharge regulations and attendant permitting (Brooks et al. 2006). For example, the 7Q10 is commonly computed and represents the lowest 7-day consecutive mean streamflow that falls below on average once every 10 years. The 10-year return period, as an example, is stated as a nonexceedance probability of 0.10, where the probability is the reciprocal of the return period. LFF analyses require a streamflow record, which in the US are typically sourced from a network of stream gauges (USGS 2023). Usually, the daily mean streamflows recorded at stream gauges are used to compute LFF statistics by fitting the base-10 logarithms of a time series of annual minimum N-day average flows to a probability distribution (Funkhouser et al. 2008; Hammett 1985; Gotvald 2016; Martin and Arihood 2010; Telis 1991; Southard 2013; Huntzinger 1978; Law et al. 2009). Averaging over N-day duration mitigates day-to-day fluctuations and smooths out low-flow data that may be influenced by diurnal or weekly variations, including those from industrial and water supply uses (Smakhtin 2001).
The reliable estimation of LFF statistics partly depends on the length of the stream gauge flow record, which is usually longer than 10 or 20 years to have a statistically sufficient sample size, but even longer records may be required to account for possible trends Blum et al. (2019). Longer record length criteria limit the locations with observational-based LFF. Furthermore, any number of discrete stream gauge locations cannot account for the indeterminate number of ungauged locations where water-resources managers and planners may need LFF statistics. For LFF estimation at locations with insufficient streamflow data and at ungauged locations, regional regression equations are commonly used. Such equations are based on statistical relations between LFF statistics at stream gauges and watershed and climatic characteristics (Feaster et al. 2020; Funkhouser et al. 2008; Martin and Arihood 2010; Wright and Ensminger 2004; Southard 2013; Law et al. 2009).
Robinson et al. (2020) Simulated Streamflow
Robinson et al. (2020) provided a data set of simulated streamflow produced from a hydrological model that used a combination of a statistical (Worland et al. 2019b) and machine-learning model approach (Worland et al. 2019a). Specifically, mean estimates for each of 15 decadal streamflow quantiles with nonexceedance probabilities that ranged from 0.0003 to 0.9997 were computed for six decades beginning in 1950 using an artificial neural network (ANN) (Worland et al. 2019a) to reconstruct the FDC at many thousands of HUC12 locations.
Subsequently, Robinson et al. (2020) used the mean estimates of the decadal quantiles to simulate daily mean streamflow for the period January 1, 1950, through December 31, 2009, by implementing the so-called QppQ method (Fennessey 1994) within the framework of copulas (Nelson 2006) following Worland et al. (2019a). The QppQ method converts streamflow for a nearby stream gauge through the flow-duration curve at the stream gauge to a probability, assuming the probabilities transfer without modification to the ungauged site, and then converts the probability to streamflow through the estimated FDC at the HUC12 location. The temporal structure between days as seen in real-world time series is removed by the estimated FDC, but the probability to probability (pp) transfer within the framework of a copula provides a scheme to restore the temporal structure (Worland et al. 2019b).
The ANN that estimated the decadal streamflow quantiles (Worland et al. 2019a) utilized information from 40 watershed and climatic characteristics and a training data set of 688 stream gauges having records with predominantly nonzero streamflow values. Importantly, daily streamflow values of zero were not mathematically predicted in the final simulated streamflow data set (Robinson et al. 2020). Therefore, biases are not only expected to be present in the streamflow predictions because of the variance reduction that is common to hydrologic model outputs (Kirby 1975; Vogel 1999), but also because of the aforementioned modeling approach.
Motivation
In 2017, the USGS, in cooperation with the USEPA, began research to statistically characterize the quantity and timing of surface water delivered to the Gulf Coast of the US as a component of research initiatives sponsored by the Gulf Coast Ecosystem Restoration Council (RESTORE Council) (RESTORE 2016). LFF analyses are key to the RESTORE initiative; however, there are places within the RESTORE study area where LFF statistics are lacking. Decreases in 7-day low flows (Dudley et al. 2020; Stephens and Bledsoe 2020) and trends in streamflow alteration (Rodgers et al. 2020) observed at the stream gauges in the study area over the last several decades further demonstrated an increased need for updated LFF statistics.
LFF statistics computed from the simulated streamflow might mitigate some obstacles that are common to LFF analyses based directly on observed streamflow—gaps in the periods of streamflow record and unequal periods of records (sample sizes) among sites—because all decades are represented and as a result, sample sizes are identical. Further, the spatial density of locations with streamflow record may limit some approaches for estimating LFF statistics (Reilly and Kroll 2003), but the production of simulated streamflow at the HUC12 level can provide a greater spatial coverage and density of locations with LFF statistics across the study area. The implementation of the bias-assessment and correction workflow has the potential to expand operational use of simulated streamflow for LFF analysis, or flow-frequency analysis more generally, because it provides a more systematic and unified platform for reporting statistics on a regional scale.
However, there are potential limitations to the use of these data including restriction to HUC12 outlets as well as bias, variance reduction in LFF statistics, and uncertainty in the GAMs. To that end, this study explores whether such issues can be mitigated. The workflow presented here has the potential to leverage existing and future simulated streamflow data sets for frequency analyses in consideration of their known limitations and provide practitioners with a way to assess if bias-corrected predictions are reliable for operational use.
Workflow Description
The workflow proposed to assess the feasibility of using streamflow simulated from a hydrologic model to estimate flow-frequency statistics is outlined as follows:
Step 1: Model output location and stream gauge matching.
Step 2: Candidate stream gauge screening.
Step 3: Streamflow record matching.
Step 4: Computation of streamflow frequency statistics.
Step 5: Scaling correction.
Step 6: Initial bias computation.
Step 7: GAM fitting.
Step 8: Bias correction.
Step 9: Workflow evaluation.
Step 10: Uncertainty analysis.
The generalized workflow is described subsequently, and the section “Practical Application of the Workflow” demonstrates the practical application of this workflow to the computation of LFF statistics from simulated streamflow provided by Robinson et al. (2020). A suite of scripts (Whaling et al. 2022) were written in the R language (R Core Team 2022) as companion software to this paper and provide publicly accessible and reproducible procedures and computations for all data preparation, manipulation, and results following Steps 1–10 specific to the practical application.
Step 1: Model Output and Stream Gauge Matching
In Step 1, stream gauges in the study area are matched to one modeling location with simulated streamflow to build a one-to-one comparison data set of stream gauge-model pairs. The comparison data set provides a foundation to compare simulated statistics with gauged flow-frequency statistics. The matching scheme can rely on an underlying hydrologic indexing system useful for aligning hydrologic data with a mapped stream network or watershed. The watershed boundary data set (WBD) (McKay et al. 2016) developed for the US, for example, is composed of HUCs that form the basis of one indexing scheme; HUCs are subdivided into successively smaller hydrologic units and indexed in such a way that information is retained about both the larger and nested watershed.
The modeling locations of the simulated streamflows exemplified in Fig. 1 are all indexed to a specific HUC watershed and associated pour point, so a suitable approach would be to search for any stream gauges located within that HUC or to match by the assigned index. Alternatively, a GIS approach could be used for spatially matching stream gauges to model output locations that are not hydrologically indexed. Inherently, this workflow applies to simulated streamflow output provided as daily records for a finite location and duration in space and time, respectively.
Step 2: Candidate Stream Gauge Screening
Candidate stream gauge screening is intended to eliminate incompatible stream gauge-model pairs identified in Step 1 and stream gauge records too short for frequency analysis; the latter is a context and user-specific choice. Requiring longer records could reduce error in the final flow-frequency statistic in some cases (Blum et al. 2019), but the minimum required record length may be limited by the availability and spatial distribution of stream gauges in the study area because record lengths in the US range from a few years to several decades long. The type of frequency analysis, such as monthly, flow-duration, flood, low-flow, and trend analysis, might also affect which stream gauges are eliminated; USGS guidance, for example, is to use a minimum of 10 years of record for flood-frequency analysis (England et al. 2019).
Importantly, screening of candidate stream gauges is based on the absolute value of the base-10 logarithm of the ratio of the network-accumulated drainage area [cumulative drainage area (CDA)] of the stream gauge watershed and the watershed represented by the modeling output location. A log-ratio criterion is hydrologically based in that it helps to ensure that both gauged and simulated streamflow records reflect similar watersheds. Stream gauges with a large difference in CDA compared with the model output location CDA need to be excluded from the analysis. A CDA log-ratio criterion of no greater than one-fourth (0.25) is suggested following Asquith et al. (2006). The criterion could be decreased to improve comparability, but too small could reduce the sample size and density of stream gauge-model pairs in the study area to an undesirable level.
Step 3: Streamflow Record Matching
Streamflow record matching is taken to help ensure comparisons between gauged and simulated flow-frequency statistics are compatible. In that regard, matching is based on the start and end dates of the period of available record as well as data gaps. For example, if there was a 3-month period where the gauge was not operational, then the simulated daily streamflow record for the same 3-month period would be removed from the analysis despite it being available. One could imagine how inclusion of the simulated streamflow could add additional uncertainty to the bias predictions, especially if the 3-month period coincided with an extreme drought that was captured in the simulated streamflow, for example.
Step 4: Computation of Streamflow-Frequency Statistics
The methodology to compute the desired flow-frequency statistics will vary based on the user’s needs. We illustrate the workflow in the context of LFF statistics, and as such, general and detailed methodologies for computing LFF statistics are provided in the section “Computation of Low-Flow Frequency Statistics” and Appendix I, respectively.
Step 5: Scaling Correction
A key aspect of the proposed workflow is to help ensure comparability between simulated and gauged flow frequency statistics for a reliable bias assessment and correction. All model output locations are unlikely to coincide where there is gauged streamflow available for direct comparison. Despite enforcing a maximum allowable log-ratio (absolute value) of the CDA in Step 2, any stream gauge-model pair having a log-ratio greater than zero is still not directly comparable because that implies the CDAs do not agree exactly and therefore neither do the watersheds. The drainage-area ratio (DAR) method (Hirsch 1979; Asquith et al. 2006) is typically used to estimate streamflow at an ungauged location by using streamflow from a nearby stream gauge with the assumption that the relation between streamflows at the ungauged and gauged sites are equivalent to the ratio of the drainage areas; in the context of this workflow, it is used to scale the gauged statistic to the model output location with a correspondingly smaller or larger CDA. The DAR method is expressed as:where = scaled gauged NQT statistic [cubic length (L) per time ()] for the ungauged (model output) location; = NQT statistic () for the stream gauge; = cumulative drainage area () for the ungauged (model output) location; = cumulative drainage area () for the stream gauge; and = exponent of unity. The value for is often assumed equal to 1, although Asquith et al. (2006) investigated this assumption and found that ranged from 0.700 to 0.935 for daily mean streamflows in Texas, and work by Asquith and Thompson (2008) found that moved away from unity for peak streamflows in Texas.
(1)
Reformulating Eq. (1) for estimation of flow-frequency statistics in base-10 logarithm units (all log-transformations in this paper are base-10 logarithms), the gauged LFF statistics are scaled to the same measure space of the simulated streamflow using Eq. (2):where = gauged LFF statistic [] computed without any adjustments; = CDA () at the simulated streamflow model output location; = CDA () at the stream gauge location; and = flow-frequency statistic [] for the stream gauge scaled by the CDA ratio.
(2)
Step 6: Initial Bias Computation
During Step 6, biases present initially in the simulated streamflow statistics (without a bias correction) are investigated to inform the practitioner how the simulated flow-frequency statistics compare with their gauged counterparts. The initial biases in the NQT statistic, [units of ] [Eq. (3)], are computed by subtracting the simulated flow-frequency statistics from the corresponding gauged flow-frequency statistics (adjusted with the DAR method in Step 5) in base-10 logarithm-space for each of stream gauge-model pairs in the comparison data set given by
(3)
The practitioner could use the initial biases to determine the average magnitude and direction of the bias in the simulated flow-frequency statistics. The mean initial bias, formulated by Eq. (4), is simply the arithmetic mean of [Eq. (3)] shown by the number of stream gauge-model pairs
(4)
Another diagnostic useful for interpreting the initial biases, [units of squared ] is computed by taking the average of squared deviations for each observation of stream gauge-model pairs from a zero-mean bias
(5)
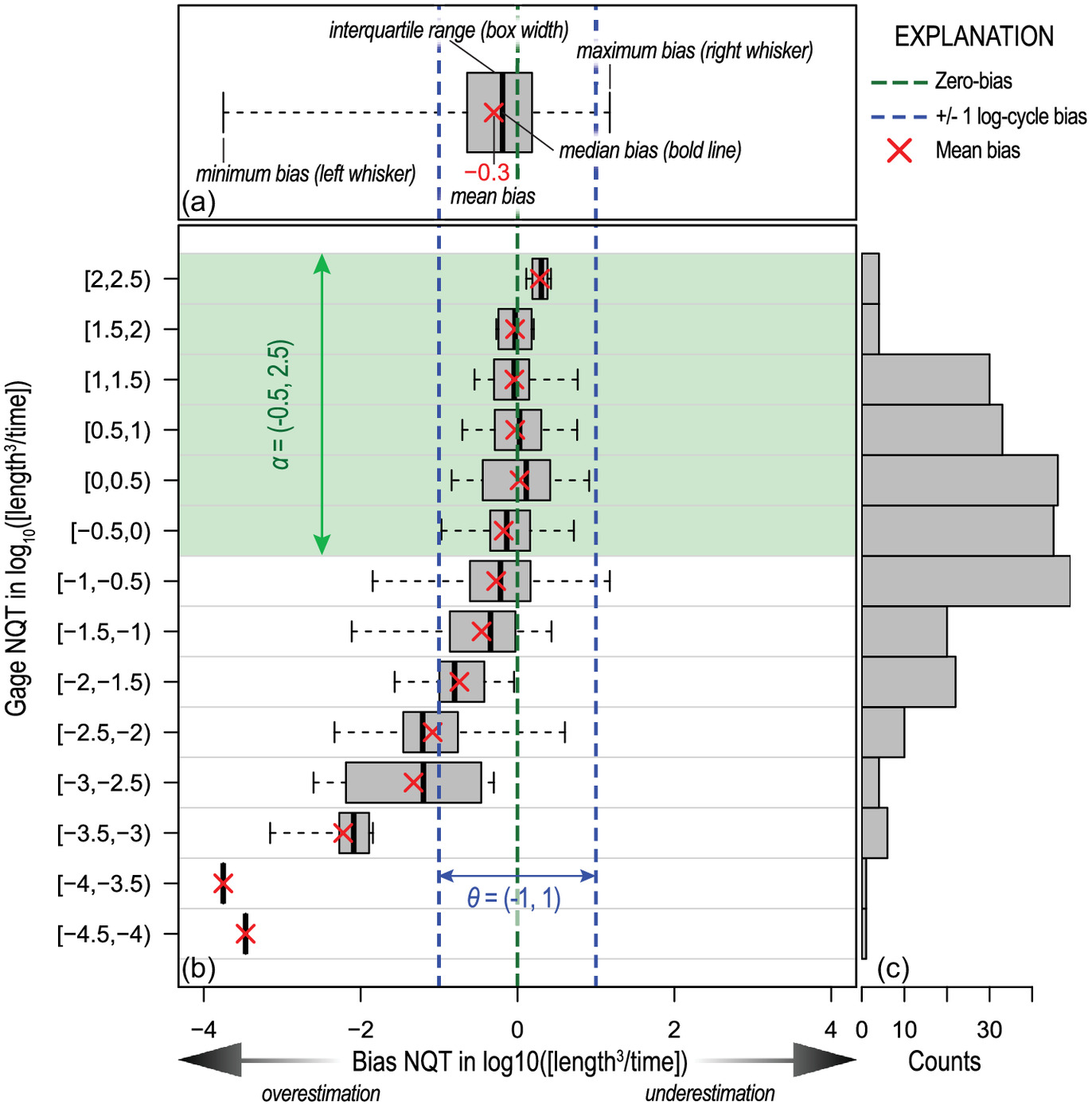
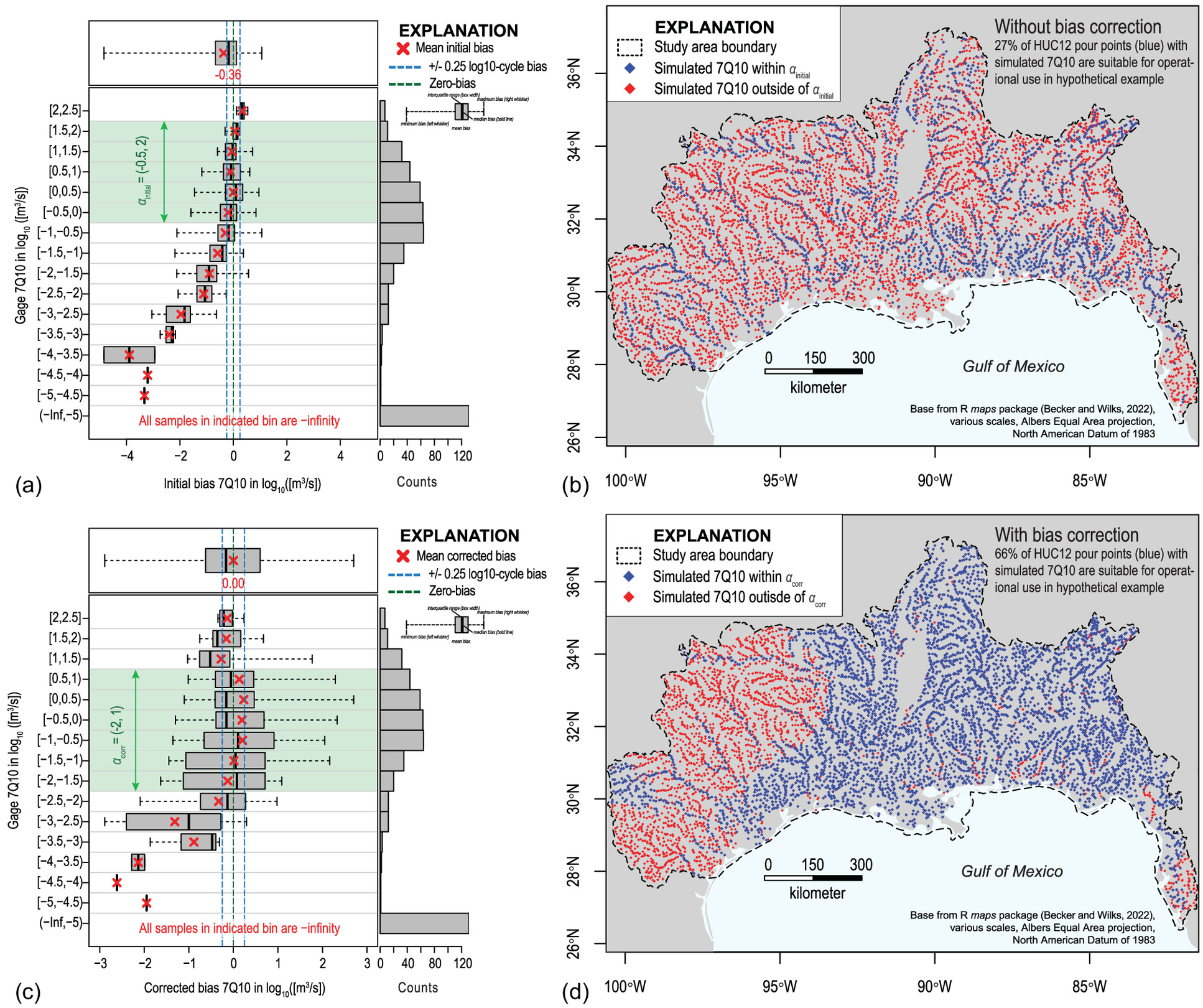
It is also important to investigate the existence of a dependent relation between the magnitude of the gauged flow-frequency statistic and the magnitude of the initial bias. As discussed in the “Introduction,” this workflow is premised on the expectation that hydrologic models generally do not reliably predict into the tails of the streamflow distribution. Thus, when simulated streamflows are cast into a flow magnitude for a selected frequency, the bias magnitude is likely to be larger for the extremely large and small magnitudes. Graphically, the relation is investigated with box and whisker plots (Chambers et al. 1983) of the bias binned by the magnitude of the gauged flow-frequency statistic (scaled by CDA ratio, ) (Fig. 3) and quantitatively assessed by recomputing for each bin (plotted as red X symbols).
Compared with the bias direction and magnitude shown by all stream gauge-model pairs [Fig. 3(a)], the individual box plots give a sense of the variability in the bias direction and magnitude with respect to binned magnitudes of the gauged flow-frequency statistic [Fig. 3(b)] and the number of observations in each bin [Fig. 3(c)]. All binned values are ideally centered near zero, indicating the simulated flow-frequency statistics are unbiased for all magnitudes of flow-frequency represented in the comparison data set. Binned values that plot to the left (negative values) and right (positive values) of the zero-bias line indicate the simulated flow-frequency statistics are being overestimated and underestimated, respectively. The bin interval (0.5 in the example shown in Fig. 3) is user-defined and depends on the range and sample size of the gauged flow-frequency statistic present in the stream gauge-model pairs; Sturges’ rule for determining the number of bins (Scott 2009) is used throughout this paper.
In terms of assessing the reliability of the simulated streamflow statistics, the binned box plots are useful for defining a number, , that specifies an interval range of the magnitude of gauged flow-frequency statistics—and by extension simulated flow-frequency statistics—considered to be unbiased. More generally, defines the magnitude range of the (initial or bias-corrected) simulated flow-frequency statistics the practitioner deems reliable for operational use; we use to denote the range determined for the initial biases and to denote the range determined for the corrected biases (more details provided in Step 9).
A modified box and whisker plot shown in Fig. 3 demonstrates how is visually determined from the plotted initial (or corrected) biases. A specification of equal to indicates that the simulated NQT statistics are reliable for any magnitude greater than and less than 2.5 base-10 logarithms of streamflow. The left and right bounds for come from the relation of the binned biases on the -axis with , a user-defined cut-off value for designating how much bias is too much. Expressed as an interval range, is the cut-off value around a bias of zero base-10 logarithms of streamflow. Accordingly, biases shall not exceed log-cycle (order of magnitude) of difference when is arbitrarily equal to one in the example. Therefore, the left bound for () is from the lower interval of the smallest -axis bin where the absolute value of minimum and maximum binned biases on the -axis do not exceed one. Similarly, the right bound for (2.5) is from the upper interval of the largest -axis bin where the absolute value of minimum and maximum binned biases on the -axis do not exceed one. However, the practitioner could use descriptive statistics other than the binned minima and maxima indicated by the box and whisker plots, such as the median, mean, or interquartile range, relative to .
One last comment is needed. Even if for the uppermost bin is unbiased, a right bound of (infinity) is not recommended because it incorrectly implies that simulated flow-frequency statistics of any magnitude are valid despite not being captured in the stream gauge-model pairs. The same logic dictates that a lower bound of would be invalid. In such cases, the largest gauged NQT statistic is suggested for the right bound, and the smallest for the left bound. However, biases are to be expected, and the remaining steps demonstrate the computation and application of a bias correction to the simulated flow frequency statistics to see if biases initially present can be mitigated.
Step 7: GAM Fitting
The characteristics of the bias shown by each NQT flow-frequency statistic are investigated by fitting thin-plate cross-validated splines to all values using GAMs (Wood 2003, 2011) in R (R Core Team 2022) using the mgcv package (Wood 2021). The GAMs are fit in two stages: Stage I is aimed at removing spatial biases that result from unmeasured covariates or structural flaws in the model that produced the simulated streamflow, and Stage II is designed to add information about the stream network back into a total bias correction. The spatial component of the Stage I GAM fitting removes information about the network, so a residual bias is assumed present that is a function of the magnitude of the simulated flow-frequency statistic, hence the need for the Stage II GAM.
The proposed two-stage GAM fitting assumes that the simulated-streamflow modeling technique preserved information about the network. Thus, the two-stage GAM fitting produces two sets of bias-correction values needed for a total bias-correction in Step 8: Stage I produces the spatial bias corrections, , and Stage II produces the residual bias corrections, . Computation of each is discussed in more detail next.
Stage I GAM Fitting
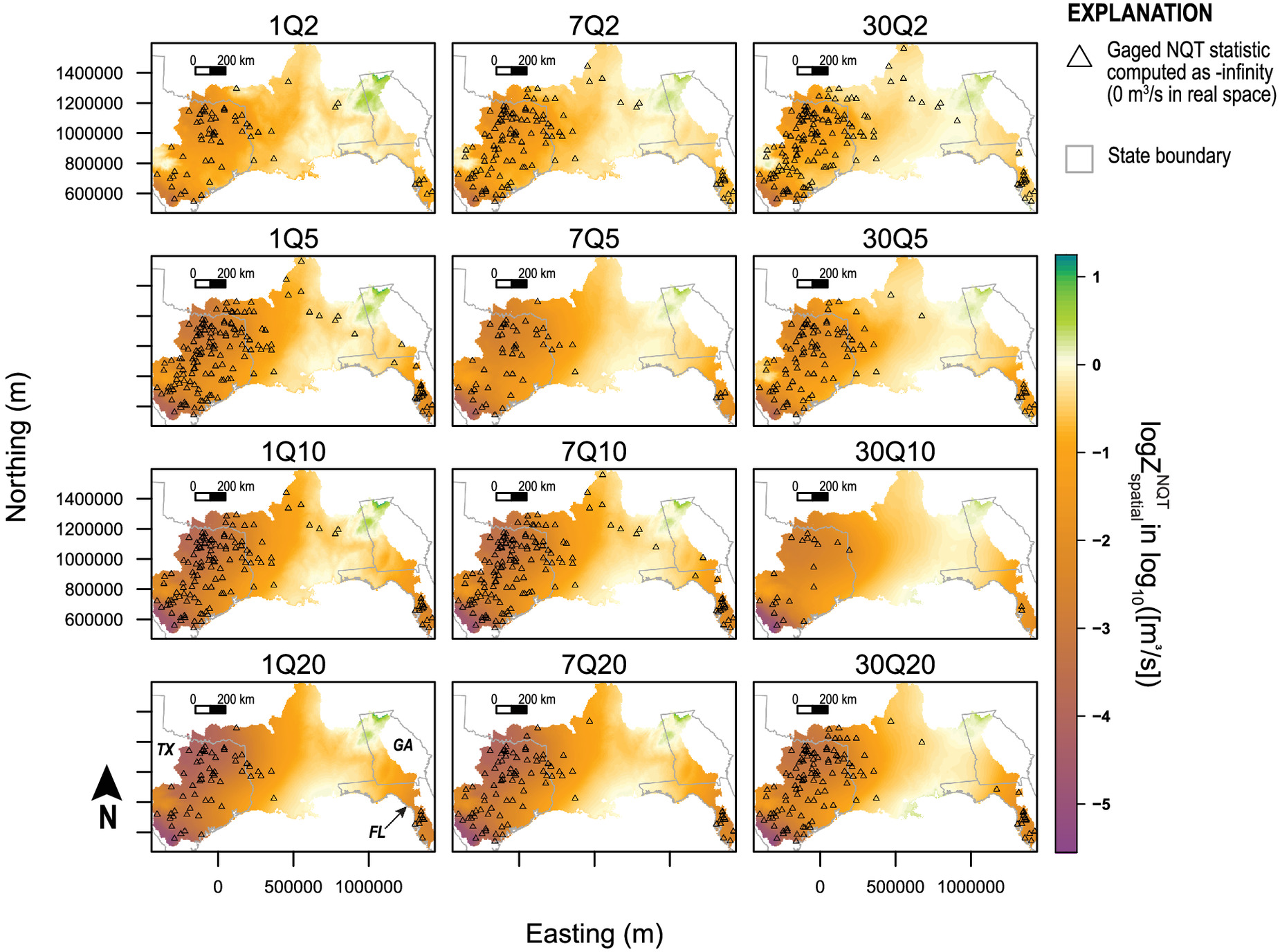
Stage I GAM fitting generates predictions of the spatial-bias correction, . Eq. (6) is a simple GAM framework that provides a rapid and effective framework to fit a surface to the stream gauge-model pair biases for each NQT flow-frequency statistic
(6)
At a minimum, all that is needed to explain the biases is the smooth [ function] (Wood 2003, 2011) on the stream gauge-model pair’s two-dimensional coordinate measured as the Universal Transverse Mercator (UTM) northing and easting; with this simple framework, the Stage I GAMs therefore represent the smoothing of the simulated streamflow model residuals in the domain of each flow-frequency statistic.
The spatial GAMs do not require any prior knowledge of the functional form of the bias and can mimic potential curvatures in data with the overall functional form while still retaining additive components. An attractive feature is that they grant flexibility to the user to account for watershed properties and or other factors not originally used as covariates in the hydrologic model. Testing of compound GAM frameworks with different distribution families (Gaussian assumed by default) and or terms in addition to the simple spatial smooth is a necessary step to this workflow if there is a strong reason to do so. Guidance for choosing an appropriate GAM framework is provided by Wood (2020).
For comparisons between frameworks for model selection, the reported deviance explained and Akaike information criterion (AIC) (Akaike 1974) are used as a measurement of goodness of fit after Asquith et al. (2017) and Dey et al. (2016), and references therein.
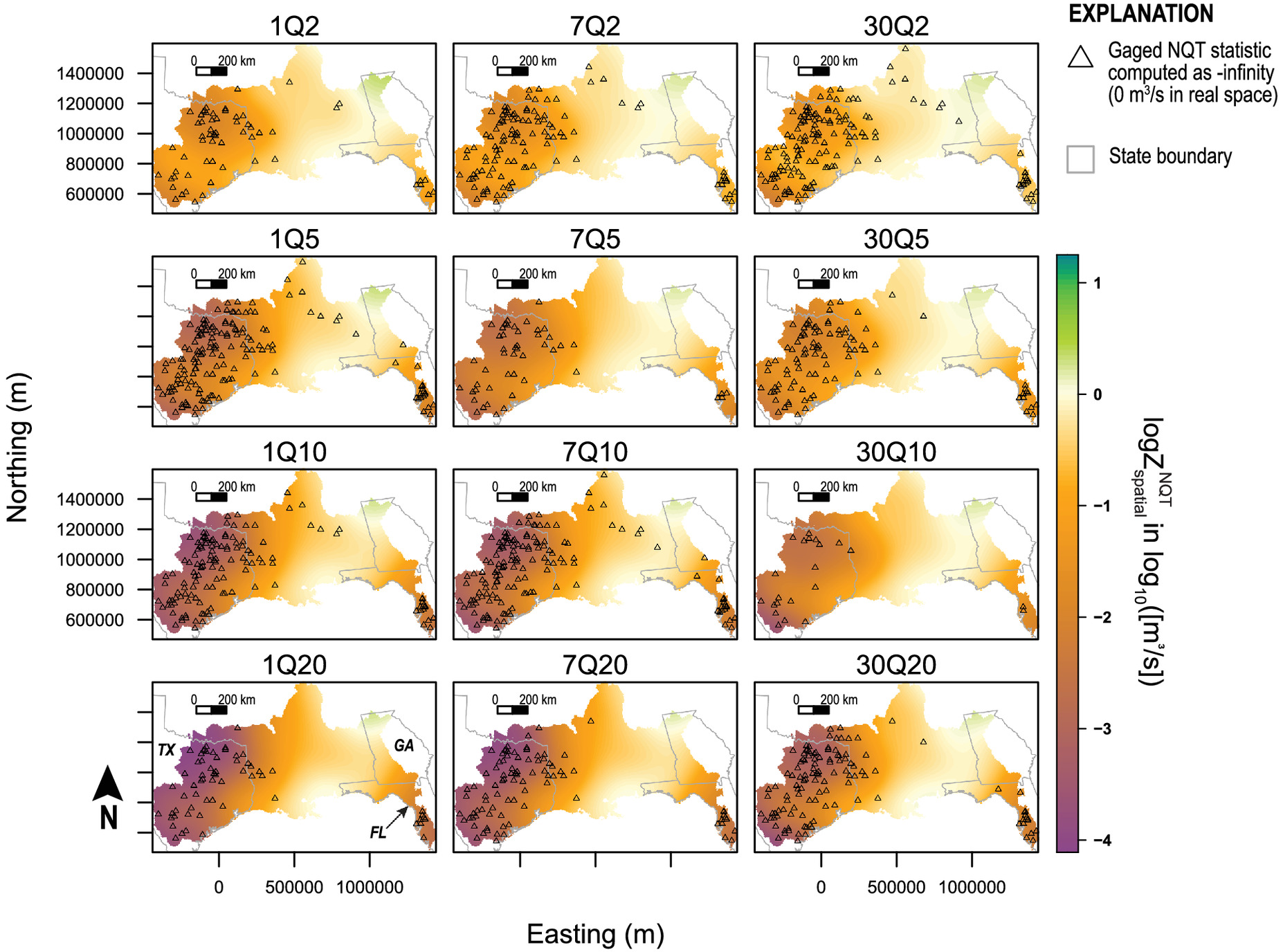
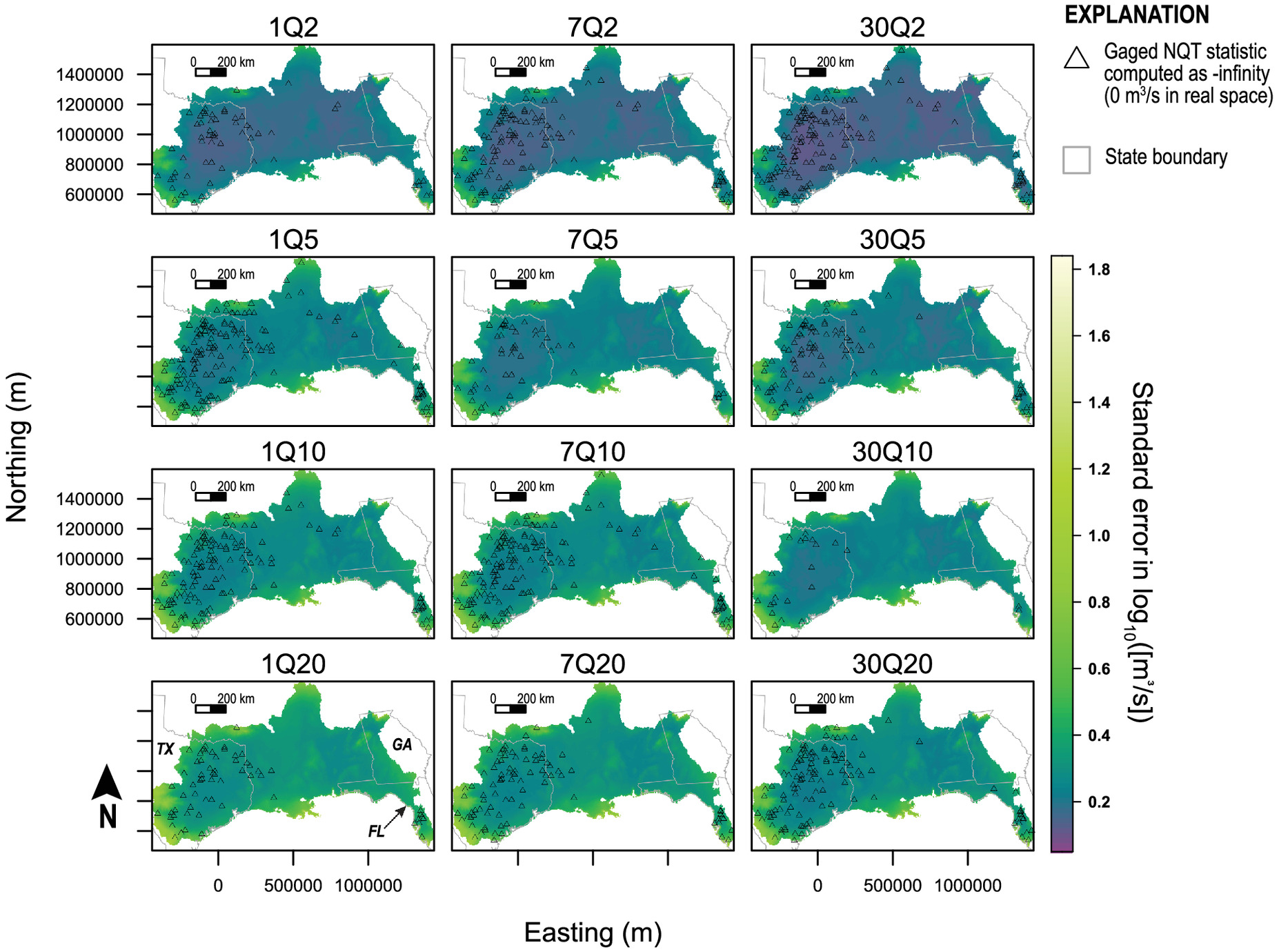
Predictions of are determined from the Stage I GAM given a set of values for the framework terms. For the simple framework, all that is needed are the eastings and northings of grid cell locations from a gridded data set (raster) where predictions are needed. The raster extent needs to encompass the spatial coverage of the stream gauge-model locations. The gridded predictions result in a surface spanning the study area that are interrogated for the spatial bias-correction values for gauged (and ungauged) model output locations. 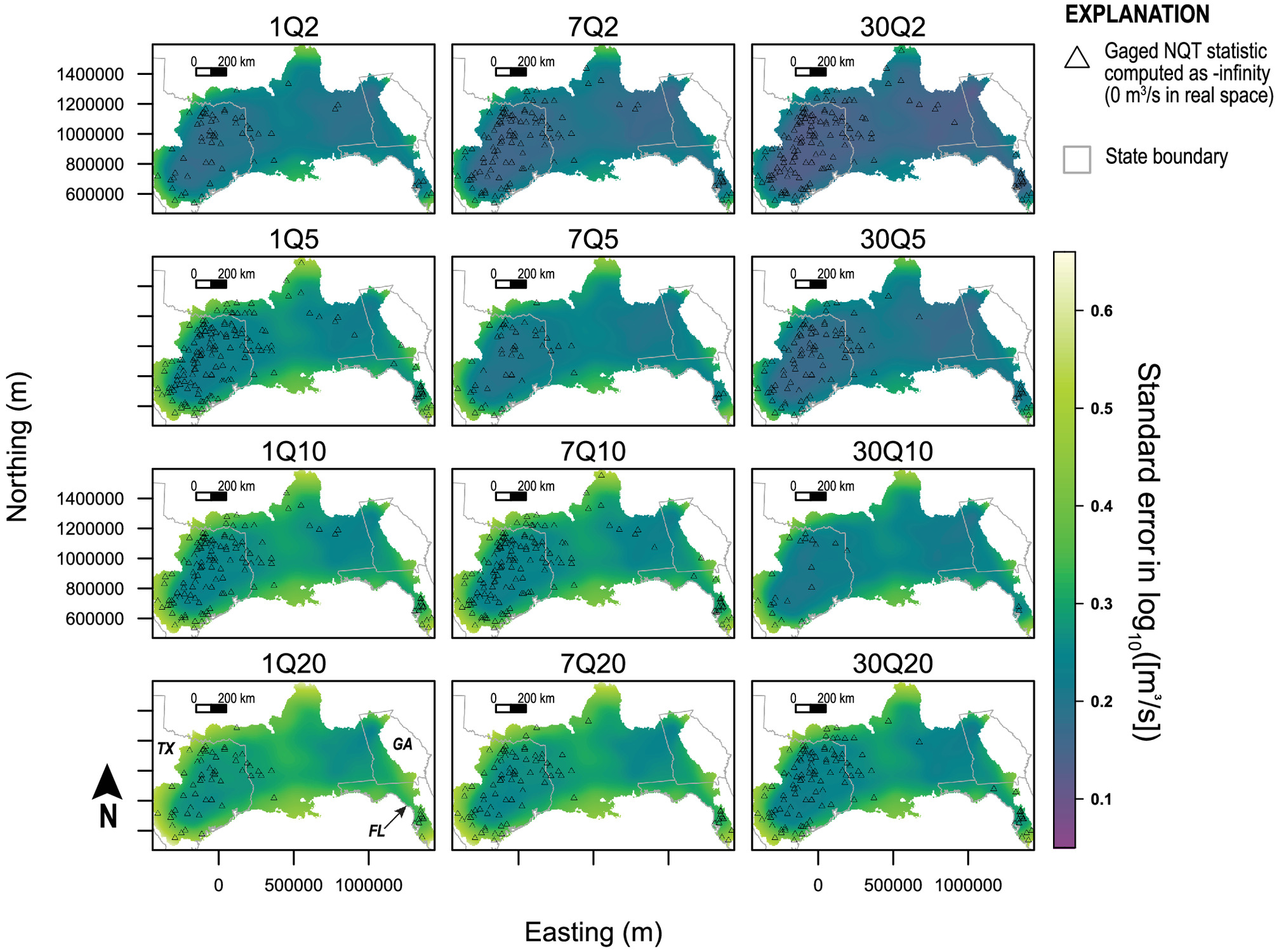Similarly, GAM standard errors of fit, which are based on the posterior distribution of the smoothing function coefficients (Wood 2021), are predicted onto the same grid for an assessment of the uncertainty with respect to space in Steps 9 and 10.
Stage II GAM Fitting
The second stage of GAM fitting removes the residual bias, , that is present after Stage I GAM fitting and subsequent application of the spatial bias correction. A residual bias is assumed because the spatial smooth term in Eq. (6) removes information about the stream network. The residual bias in the NQT flow-frequency statistic is computed following Eq. (7) for each of stream gauge-model pairs:where the spatial bias correction is the cell value from gridded predictions made by Stage I GAM corresponding to the NQT flow-frequency statistic of interest (for example, use the 7Q2 raster to correct the initial simulated 7Q2) at some easting and northing of each stream gauge-model pair location. The raster cell value at the model output location is determined with GIS software or geospatial functions as implemented by Whaling et al. (2022).
(7)
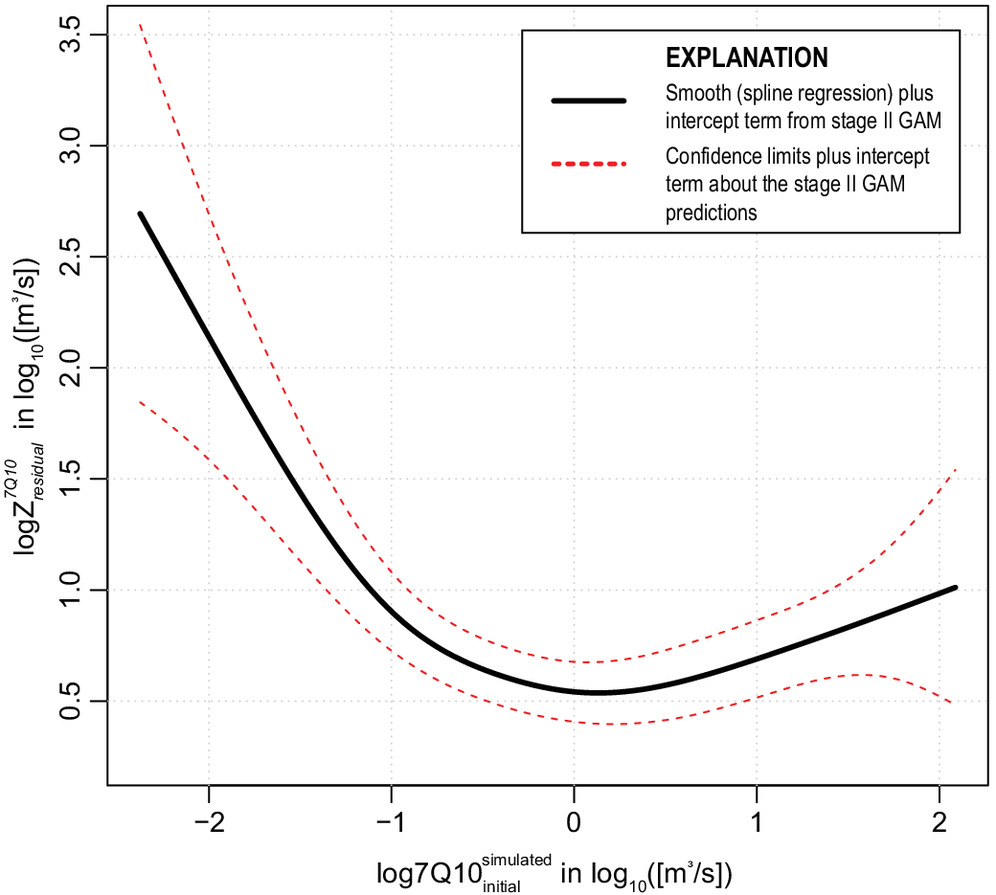
The second-stage GAM is then fitted from the resulting stream gauge-model residual bias with the following framework, which assumes a Gaussian distribution family on all finite values of :
(8)
The fitted Stage II GAM produces a smooth (spline regression) that relates the magnitude of to a prediction for , with accounting for the intercept term output from the fitted GAM. Extrapolation to and with linear interpolation is suggested in the event that the stream gauge-model pairs do not encompass the extrema of .
Step 8: Bias Correction
The sought-after total bias correction in base-10 logarithm units of streamflow for the NQT flow-frequency statistic, , is simply the sum of the spatial bias correction from Stage I, , and the residual bias correction from Stage II, , formulated by Eq. (9)
(9)
The application of the total bias correction to the simulated NQT LFF statistics is formulated by Eq. (10)for each of stream gauge-model pairs or ungauged modeling locations. Total bias corrections are applied on two separate occasions in this workflow—during the workflow evaluation in Step 9 for just the stream gauge-model pairs—and again for computing the bias-corrected simulated flow-frequency statistics for all modeling locations after Step 9 once a particular GAM framework is deemed effective.
(10)
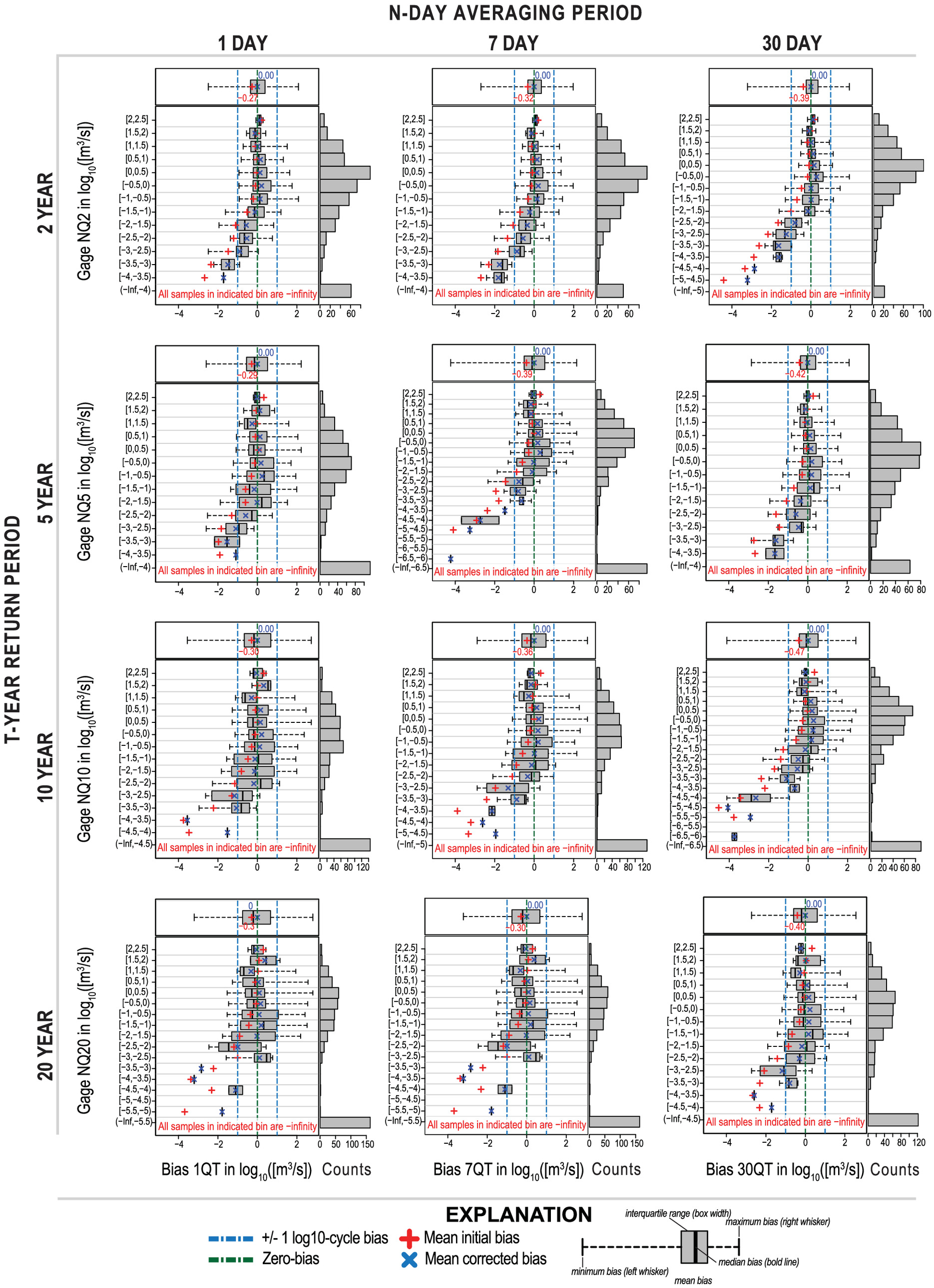
Step 9: Workflow Evaluation
As a first-order evaluation, the corrected bias (), mean corrected bias (), and the bias-corrected variance from a mean bias of zero, , is recomputed for the NQT statistic following Eqs. (3)–(5), respectively, by replacing all values of in the equations with the values of [Eq. (10)] determined for the stream gauge-model comparison data set. Values closer to zero are desired because it indicates the workflow effectively removed modeling residuals. However, where biases remain, the efficacy of the two-stage GAM process in removing the bias needs to be thoroughly evaluated, and further guidance is detailed subsequently.
Once a GAM framework has been selected that minimizes (absolute value), the practitioner can return to Step 8 and compute bias-corrected LFF statistics for all model output locations with simulated streamflow in the study area. Then, the workflow evaluation is focused on determining if the bias predictions apply to all bias-corrected flow-frequency statistics.
In terms of assessing the reliability of the bias-corrected simulated streamflow statistics, binned box plots, as suggested in Step 6, are useful. Similar to , is defined to specify the magnitude range of the bias-corrected simulated flow-frequency statistics considered as reliable for operational use, assuming that biases are still present after the correction scheme.
The first-stage GAM is used to explore the magnitude and spatial distribution of the spatial bias exhibited by the simulated flow-frequency statistics. Generally, maps of the spatial bias reveal where underestimation and overestimation occur in the study area and may provide conceptual feedback for testing of additional covariates in a compound Stage I GAM framework. Evaluation of the maps of the standard errors of fit (Step 7) are suitable for the semi-quantitative discussion about relative spatial GAM performance throughout the study area. In particular, they may help identify where estimates are unreliable because of poor stream gauge-model density.
Step 10: Uncertainty Analysis
Reporting of uncertainty is a necessary step in this workflow. The outcome of Step 10 is the production of some type of credible prediction limits unique for each modeling location in the domain of the desired statistic. To clarify, the computed 95% prediction limits for any one prediction do not provide a span containing the true mean statistic value with 95% probability but rather the limits so constructed to encompass the statistic 95% of the time (Good and Hardin 2012).
The uncertainty analyses used for computation of 95% prediction limits is algorithmically straightforward although subject to several assumptions and ignored terms. A normal distribution of the log-transformed predictions is assumed applicable, and the final flow-frequency statistic is its mean. The applicable standard deviation is thus the core of the problem.
The variance of the predictions is assumed to stem from two sources, the statistical variance of the flow-frequency statistic and the two-stage GAM bias-prediction variance. Other sources of uncertainty are assumed negligible. Using a bootstrapping technique from Efron and Tibshirani (1985), the statistical variance for each, , simulated NQT LFF statistic, , is estimated from a simulated population of the NQT statistic of interest. To create the simulated population, first, a sampled time series of flows is generated from the original time series intended for the flow-frequency analysis. Random sampling with replacement is recommended so that the sampled series size is equal to the size of the original series. Then, the NQT statistic is computed from the sample using the same methodology the user opted to employ in Step 4. The simulation is repeated many times (ideally thousands), and the desired statistical variance is computed from the simulated population.
The distribution and method of parameter estimation choices specific to the computation of the desired flow-frequency statistics are assumed to be correct in this workflow. However, Asquith et al. (2017) discussed estimation difficulties with frequency analyses wherein additional uncertainties stem from the choice of the parameter probability distribution among reasonable candidates, and differing methods of parameter estimation (product moments, L-moments, maximum likelihood, and maximum product of spacing) will estimate differing distribution parameters for the same sample.
Uncertainty in the bias corrections can be conceptualized in several ways and, two options are provided. The bias corrections themselves are assumed as correct with only uncertainty stemming from prediction specific computations from the GAMs, and each prediction has a unique associated variance. Alternatively, bias corrections are assumed as incorrect and any residual bias in contributes to a global variance in the final bias-corrected simulated flow-frequency statistic. The derivation may depend on the distribution family supplied in the spatial GAM framework. For the Gaussian case, the global scale of the GAM and its standard errors of fit (Step 7) unique for each prediction are combined through the salient mathematics of prediction intervals for a GAM (Asquith 2020 and software documentation therein). Alternatively, the variance of from a mean bias of zero, , may serve as a reasonable estimate for a global GAM prediction variance. The formulation is structurally identical with that of in Eq. (5).
The two aforementioned variances, namely, statistical from the flow-frequency computations, , and bias-correction from the Stage I and II GAM predictions, , are used to compute , the standard deviation for an individual simulated flow-frequency statistic, , following Eq. (11)
(11)
In the preceding equation, if is specified as , then the second term is a constant for all (NQT) simulated flow-frequency statistics.
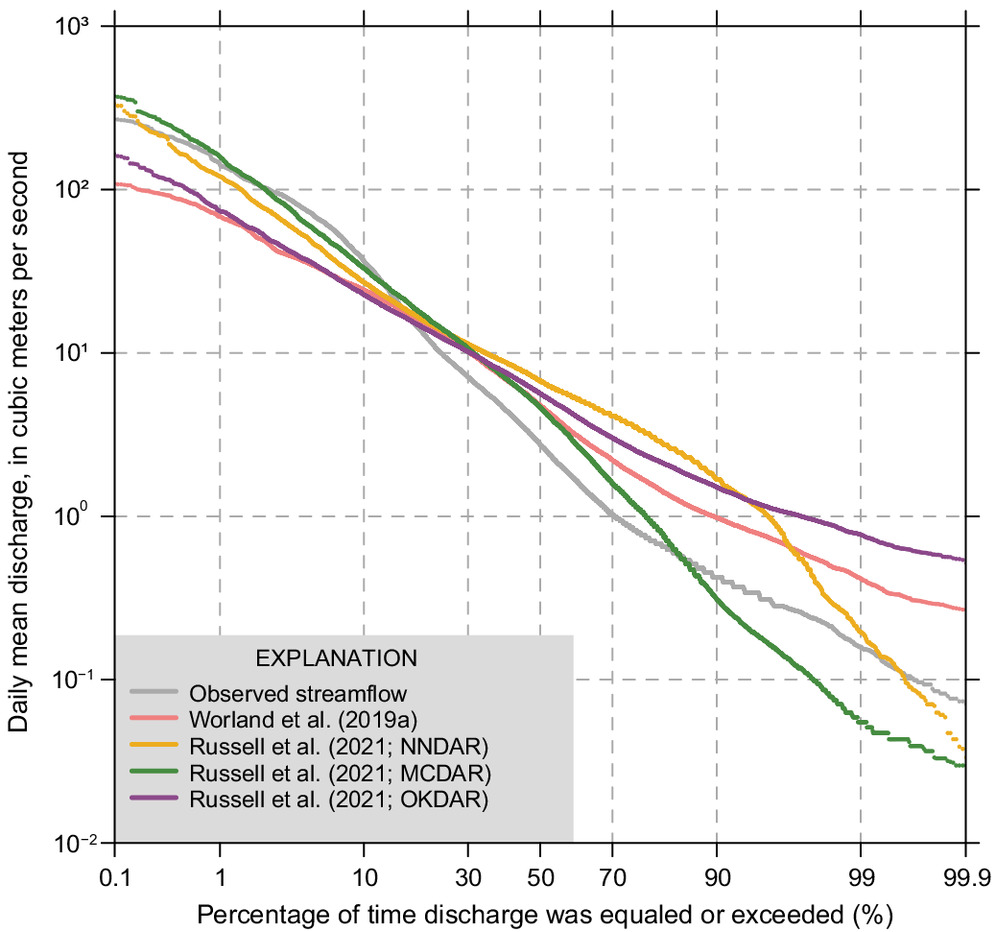
Using the result of , the 2.5% and 97.5% quantiles are computed from the normal distribution, which together represent the 95% prediction limits. One last caveat is needed. The uncertainty approach here does not attempt to propagate uncertainty into the flow-frequency statistic from the simulated daily values themselves. For example, the 95% prediction limits from Robinson et al. (2020) would generally be too small because of variance reduction inherent to simulated streamflow from data-driven hydrologic models. Furthermore, the proposed computation of uncertainty is flexible so that it can be applied to comparisons between multiple simulated streamflow data sets that are being explored for operational use, especially given that model uncertainties are not reported in a standardized way, or they might not be reported at all.
Practical Application of the Workflow
The proposed workflow is applied to the Robinson et al. (2020) simulated streamflow in the context of assessing simulated LFF statistics for operational use. All data preparation, manipulation, and results following Steps 1–10 are documented in the companion software (Whaling et al. 2022). Details regarding the specifics of the workflow applied to this context are discussed in the “Methods” section up to Step 7, GAM fitting. A comparison between GAM frameworks, the characteristics of the initial and corrected biases, and uncertainty analysis is presented in the “Results” section, followed by an evaluation of the efficacy of the workflow and the potential applications in operational hydrology in the “Discussion” section.
Methods
Building the Stream Gauge-Model Comparison Data Set
The Robinson et al. (2020) data set is conveniently organized by HUC12, so the comparison data set of stream gauge-model pairs was based on the HUC12 watershed boundary (McKay et al. 2016) in which the stream gauge is located in following Step 1. A one-fourth (0.25) absolute log-ratio CDA criterion was used to remove incompatible stream gauge model pairs in Step 2; for simplicity, we assumed the one-fourth criterion is small enough to justify in Eq. (2) in Step 6 such that drainage area differences between the gauge and HUC12 watersheds are similar in practical applications following qualitative guidance from Asquith et al. (2006).
Candidate stream gauges were also screened for outliers, such as misreported HUC12s and CDAs. A minimum of 20 years of records was chosen for candidate stream gauge selection. The 20-year criteria balances the need for statistically sufficient gauged record length for reliable frequency analysis in Step 4, as well as the number of stream gauge-model pairs for the bias assessment. A terminal list of 497 stream gauge-model pairs were identified (Fig. 2).
In Step 3, streamflow record-matching was accomplished through matching available climate years between the simulated and gauged N-day annual minima series. First, the dataretrieval package (De Cicco et al. 2022) was used to download gauged daily streamflow from the USGS National Water Information System (NWIS) database (USGS 2023) for each stream gauge-model pair and for the same period of record for which the simulated streamflow was predicted. Then, the 1, 7, and 30-day annual minima were computed for each of the 497 stream gauge-model pairs from the N-day moving averages using the DVstats R package (Lorenz 2017). Annual minima that were computed with fewer than or equal to 275 days of record in the climate year (75% of the year) were removed from both series to help ensure that the resulting statistics are directly comparable.
For all missing gauged annual minimum, or, annual minimum computed with less than or equal to 75% of gauged record, the annual minima in the gauged series was removed as well as annual minima for the corresponding climate year in the matching simulated series. This means that if the full study period was available in the gauged series, the maximum possible record length of annual minima was 59 years (climate years 1951–2009).
Computation of Low-Flow Frequency Statistics
In Step 4, 12 LFF statistics (1Q2, 1Q5, 1Q10, 1Q20, 7Q2, 7Q5, 7Q10, 7Q20, 30Q2, 30Q5, 30Q10, and 30Q20) were computed for each stream gauge-model pair. Generally, computation of LFF statistics starts with the base-10 log-transformation of the series of N-day annual minima to mitigate for skewness; this was followed by computation of L-moments and then parameter estimation for the PE3 distribution. Computational difficulties in the procedure to compute the LFF statistics arose when there were zero-flow observations () in the annual minimum series, which equates to after the log-transformation step. These difficulties were treated situationally and only existed for the gauged series because the ANN model inherently did not predict FDCs with zero-flow values (section Robinson et al. (2020) Simulated Streamflow).
Specifically, a degenerate annual minimum series defined as having zero-flow observations were treated with (1) either an enforcement that the gauged LFF statistic is when there were too few nonzero annual minima to compute L-moments, or (2) with a conditional probability adjustment when some zeros were present, but enough nonzero annual minima to compute L-moments. In the latter case, annual minima equal to were censored from the N-day series and the smallest nonzero annual minima in the series was used as a truncation threshold in order to remap the full-range probability into the range within the noncensored part of the tail. Additional details and justification for the approach used herein are provided in Appendix I.
Initial Bias Computation
After applying the scaling correction to the gauge LFF statistics outlined in Step 5, LFF statistics were subtracted following Eq. (3). An important remark is that some values of were computed as because the gauged LFF statistic was computed to be (section “Computation of Low-Flow Frequency Statistics” and Appendix I). These stream gauge-model pairs are incorporated in the bias modeling with a censoring strategy (section “GAM Framework Selection and Fitting”), but they cannot be included in the computations of the initial nor corrected mean and variance of the biases [Eqs. (4) and (5)].
GAM Framework Selection and Fitting
For Stage I GAM fitting (Step 7), several model formulas were tested, but two frameworks are compared here, namely, the simple GAM framework [Eq. (6)] that uses a smooth on the spatial terms and a compound framework [Eq. (12)] to demonstrate testing of additive terms. Both GAM frameworks keep the initial biases in logarithmic units to mitigate for extreme skewness. Because computational issues arise when infinite values are supplied to the GAM, both frameworks also enforce a censored normal distribution of the biases to indirectly incorporate the values of that were evaluated as . The censoring is based on a situational awareness of Worland et al. (2019a) modeling choices, namely, the fact that the ANN model inherently did not predict FDCs with zero-flow values. Because all simulated LFF statistics are nonzero, any value computed from a stream gauge-model pair where the gauged statistic was will always be characterized by overestimation of the resulting simulated streamflow statistic. Thus, values that evaluated to are incorporated into the GAM as imputed left-censored values. In practice, substituting the values with an infinitesimally small value is computationally inefficient, so the imputed value was based on the limit to which differences in daily streamflow, and LFF statistics by extension, are measured, which we assume is , or approximately in base-10 logarithms ().
To re-emphasize, the Stage I GAM framework selection allows one to explore spatial biases and correct for unmeasured covariates and structural flaws related to the hydrologic model that simulated streamflow. The choice to use a censored normal distribution in the GAM framework, as opposed to removing the biases, may deal with the Worland et al. (2019a) modeling choices. Any of the 40 watershed and climatic characteristics that Worland et al. (2019a) already used as covariates are not expected to meaningfully improve the Stage I GAM performance beyond the simple two-dimensional estimation by stream gauge-model location. Drainage area, for example, was already identified as a strong predictor of streamflow and incorporated as a covariate in the ANN (Worland et al. 2019a); drainage area is therefore not expected to explain the bias leftover from the model and testing confirmed as much (Whaling et al. 2022).
There are additional unmeasured covariates such as potential evapotranspiration (PET) that were not used in the ANN that simulated the streamflow tested herein. Given that PET is an important predictor for streamflow in the study area (Markstrom et al. 2016), PET could be a surrogate for other unmeasured covariates of not only climatology but also terrain, distance to moisture source, and others, and as such, it may explain some of the modeling residuals in the low-flow domain. We tested the following compound framework in addition to the simple framework outlined in Step 7 [Eq. (6)] to demonstrate testing of additive terms:which uses the tensor product smooths and interactions [ function] (Wood 2003, 2011) between the two-dimensional stream gauge-model pair locations (first term supplied to ) and one-dimensional PET (second term supplied to ). PET predictions for the study area were downloaded as gridded data sets of the monthly average from 1895 to present (NOAA and National Centers for Environmental Information 2023). The September average of the study period (1950–2009) predictions were used as input to the GAM because the mean date of occurrence of annual low flows in most of the study area historically occurs in September (Floriancic et al. 2021).
(12)
We then fit the spatial GAMs using the two frameworks selected for testing to generate two sets of spatial bias corrections and standard error of fit predictions. The easting and northing locations from a 1-km national-scale grid (Clark et al. 2018) was used, cropped to the study area (Fig. 2). Following application of the spatial correction from the Stage I GAM frameworks tested, the Stage II GAMs were created from the residual bias as a function of the magnitude of the simulated LFF statistic estimate itself [Eq. (8)]. Two sets of total bias corrections were computed [Eq. (9)] for the analysis, each stemming from the simple and compound spatial GAM frameworks tested.
Results
Stream Gauge-Model Pair Initial Bias
Values of reported in Table 1 (Column 6) are negative for each LFF statistic, which indicates, on average, an overestimated simulated LFF statistic compared with its matching stream gauge as dictated by Eq. (3). The magnitude of overestimation ranged from about a quarter to a half base-10 log cycle. According to values of compared by its T-year return period in Table 1 (1Q2 versus 7Q2 versus 30Q2, for example), the magnitude of overestimation increased with increasing N-day averaging period; compared by N-day averaging periods (1Q2 versus 1Q5 versus 1Q10 versus 1Q20, for example), the magnitude of overestimation increased between the 2- and 5-year return periods and decreased between the 10- and 20-year return period. The largest (absolute) amount of overprediction (Minimum , Column 4 in Table 1) occurred for the 7Q5 at nearly seven base-10 logarithm , and the least amount of overprediction occurred for the 1Q2, whereas the largest amount of underprediction (Maximum , Column 5 in Table 1) was around an order of magnitude for each LFF statistic. Values of binned by the magnitude of the gauged LFF statistic in Fig. 4 (red X symbols) show that simulated LFF statistics tend to be initially overestimated for the corresponding gauged LFF statistics smaller than zero base-10 logarithm (that is, ), and unbiased for gauged LFF statistics greater than or equal to zero. There is also some slight underestimation in the uppermost [2, 2.5] base-10 logarithm bin.
| LFF statistic | Number gauges with LFF statistic equal to | Number of positive | Number of negative | Minimum | Maximum | ||
|---|---|---|---|---|---|---|---|
| 1Q2 | 61 | 168 | 329 | 1.10 | 0.47 | ||
| 1Q5 | 114 | 145 | 352 | 1.19 | 0.52 | ||
| 1Q10 | 145 | 134 | 363 | 1.18 | 0.59 | ||
| 1Q20 | 163 | 125 | 372 | 1.14 | 0.58 | ||
| 7Q2 | 50 | 151 | 346 | 0.93 | 0.50 | ||
| 7Q5 | 95 | 135 | 362 | 1.03 | 0.79 | ||
| 7Q10 | 131 | 129 | 368 | 1.06 | 0.70 | ||
| 7Q20 | 151 | 128 | 369 | 1.07 | 0.66 | ||
| 30Q2 | 22 | 150 | 347 | 0.79 | 0.67 | ||
| 30Q5 | 63 | 139 | 358 | 0.91 | 0.69 | ||
| 30Q10 | 90 | 128 | 369 | 0.95 | 1.02 | ||
| 30Q20 | 122 | 125 | 372 | 0.96 | 0.73 |
Note: Rows are labeled by the low-flow frequency statistic (LFF). NQT = low flow (streamflow), Q, for N-day duration and T-year return period. Data columns 1 and 2 correspond to a number out of a terminal list of 497 stream gauge-model pairs. The remaining columns contain data reported in units of , except for Column 7, which is reported in squared units of .
The for each LFF statistic is determined from a variable subset of stream gauge-model pairs from the terminal list of 497 because of complications in computing LFF from a gauged series with an abundance of zero-flow values (section “Initial Bias Computation”). The number of stream gauge-model pairs where the gauged LFF statistic was computed as is provided in Table 1 (Column 1) and also represented graphically in Fig. 4 (Counts corresponding to the lowermost bin for each LFF statistic). Generally, the number of observations increased with decreasing N-day averaging period and increasing return period.
GAM Comparison
For both the simple [Eq. (6)] and compound [Eq. (12)] Stage I GAM frameworks tested, the -values for the spatial term were statistically significant (significance level, alpha = 0.05). In the compound framework, the PET term was also statistically significant and explained an additional 0.24% to 3.11% of deviance (averaging 1.09%), and was associated with lower AIC values as presented in Table 2. After ruling out overfitting as the reason for the higher standard errors of fit observed in the compound framework compared with the simple framework (also detailed in Table 2), these findings indicate that the compound framework slightly outperformed the simple framework.
| LFF statistic | Deviance explained (%) | AIC | Minimum SE of fit | Maximum SE of fit |
|---|---|---|---|---|
| Simple GAM framework [Eq. (6)] | ||||
| 1Q2 | 21.7 | 1,584 | 0.17 | 0.45 |
| 1Q5 | 26.2 | 1,678 | 0.21 | 0.55 |
| 1Q10 | 29.3 | 1,660 | 0.23 | 0.60 |
| 1Q20 | 32.4 | 1,622 | 0.25 | 0.66 |
| 7Q2 | 23.8 | 1,497 | 0.15 | 0.40 |
| 7Q5 | 26.6 | 1,655 | 0.19 | 0.50 |
| 7Q10 | 30.2 | 1,651 | 0.22 | 0.59 |
| 7Q20 | 32.0 | 1,630 | 0.23 | 0.63 |
| 30Q2 | 28.6 | 1,277 | 0.12 | 0.35 |
| 30Q5 | 27.2 | 1,543 | 0.16 | 0.42 |
| 30Q10 | 30.9 | 1,625 | 0.19 | 0.53 |
| 30Q20 | 33.9 | 1,613 | 0.21 | 0.59 |
| Compound GAM framework [Eq. (12)] | ||||
| 1Q2 | 22.5 | 1,577 | 0.14 | 1.38 |
| 1Q5 | 26.4 | 1,678 | 0.20 | 1.29 |
| 1Q10 | 29.7 | 1,659 | 0.22 | 1.39 |
| 1Q20 | 33.3 | 1,621 | 0.25 | 1.84 |
| 7Q2 | 25.4 | 1,489 | 0.13 | 1.31 |
| 7Q5 | 27.4 | 1,653 | 0.18 | 1.21 |
| 7Q10 | 30.6 | 1,651 | 0.22 | 1.42 |
| 7Q20 | 32.6 | 1,630 | 0.24 | 1.64 |
| 30Q2 | 31.3 | 1,262 | 0.11 | 1.22 |
| 30Q5 | 30.3 | 1,531 | 0.16 | 1.69 |
| 30Q10 | 31.9 | 1,621 | 0.19 | 1.36 |
| 30Q20 | 34.5 | 1,613 | 0.22 | 1.55 |
Note: Rows are labeled by the low-flow frequency statistic (LFF). NQT = low flow (streamflow), Q, for N-day duration and T-year return period. AIC = Akaike information criterion; and SE = standard errors.
As a result, the remainder of this paper primarily discusses the results obtained using the compound framework, with findings related to the simple framework detailed in Appendix II. However, both GAM frameworks effectively remove modeling residuals from Worland et al. (2019a) on average, as evidenced by the computed values of provided in Table 3 (compound framework) and Appendix II (simple framework). The similarity in the magnitude and direction of between the two frameworks yet (slightly) different performance metrics likely means that the PET in the compound Stage I GAM framework explains more deviance in the censored values equal to which are not represented in the mean (section “Initial Bias Computation”), but are included as censored values in the compound Stage I GAM framework (section “GAM Framework Selection and Fitting”).
| LFF statistic | Mean | Mean | Minimum | Maximum | Mean | Mean gauge 95% PL width | Mean HUC12 95% PL width | Minimum | Maximum | |||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1Q2 | 0.40 | 1.01 | 0.26 | 2.47 | 0.40 | 2.08 | ||||||
| 1Q5 | 0.77 | 1.55 | 0.32 | 3.32 | 0.72 | 2.22 | ||||||
| 1Q10 | 0.98 | 1.86 | 0.40 | 3.97 | 1.03 | 2.73 | ||||||
| 1Q20 | 1.06 | 1.82 | 0.47 | 4.30 | 1.20 | 2.81 | ||||||
| 7Q2 | 0.29 | 0.63 | 0.27 | 2.41 | 0.38 | 1.98 | ||||||
| 7Q5 | 0.59 | 1.06 | 0.37 | 3.35 | 0.73 | 2.15 | ||||||
| 7Q10 | 0.84 | 1.37 | 0.41 | 3.76 | 0.92 | 2.70 | ||||||
| 7Q20 | 0.94 | 1.46 | 0.50 | 4.02 | 1.05 | 2.79 | ||||||
| 30Q2 | 0.11 | 0.41 | 0.31 | 2.38 | 0.37 | 1.95 | ||||||
| 30Q5 | 0.35 | 0.64 | 0.37 | 2.69 | 0.47 | 2.10 | ||||||
| 30Q10 | 0.50 | 0.97 | 0.49 | 3.51 | 0.80 | 2.41 | ||||||
| 30Q20 | 0.70 | 1.23 | 0.51 | 3.61 | 0.84 | 2.57 |
Note: Rows are labeled by LFF. The last data column contains values of for each LFF statistic from Table 1 to facilitate comparisons with . PL = prediction limit.
Total Bias Correction
Using the compound Stage I GAM framework [Eq. (12)] to explore the spatial bias, most of the study area is characterized by negative values of for all NQT statistics (Fig. 5), which indicates a downward correction when applied to the simulated LFF statistic [Eq. (10)] at those locations because the LFF statistic was predicted to be overestimated. In contrast, positive values of indicate an upward correction for underestimated LFF statistics. Bias corrections of and greater in the western region of study area into Texas and in Florida (Fig. 5) represents a full order of magnitude (or more) downward correction. Underestimation of simulated LFF statistics covers a smaller portion of the study area, but there is consistent underestimation seen in the HUC12 watersheds located in the northeast region of the study area in Georgia, and along the Gulf coast extending from eastern border of Texas to western Florida for all LFF statistics (Fig. 5). Bias values near zero (unbiased) occur in the east-central interior of the study area (light yellow colors in Fig. 5).
Visualization of the Stage I GAM also demonstrates the importance of implementation of an additional GAM in the second stage. The spatial corrections are regionalized, and therefore not network-aware, so the residual correction is needed to ensure the final corrections honor the network that the modeling of Worland et al. (2019a) embedded in the daily streamflows. To provide an example, Fig. 6 shows the smooth for determining the 7Q10 residual bias plotted with confidence limits about the Stage II GAM predictions [the data and outputs used to construct the final smooths for all 12 LFF statistics are available from Whaling et al. (2022)]. For the 7Q10, and generally for the other LFF statistics, a larger correction is needed for the extremely low and high magnitude simulated LFF statistics.
Table 3 indicates that the magnitude of (Column 1) is larger than the magnitude of (Column 2) on average; therefore, when the two biases are summed to arrive at the total bias correction [Eq. (9)], the magnitude of becomes dominated by the spatial bias correction, on average (Column 5). In terms of absolute value, the magnitude of total overestimation was largest for the 30-day averaging period (Table 3, Column 3); total underestimation was largest for the 1-day averaging period (Table 3, Column 4).
Stream Gauge-Model Pair Corrected Bias
Values of reported in Table 3 (Column 11) for the compound Stage I GAM framework are near zero but slightly negative for each LFF statistic. The magnitude of the corrected mean bias is smaller than the values of (Table 1, Column 6; duplicated in Table 3), which indicates substantial improvement with the bias-correction workflow. Values of that are closer to zero indicate a better handling and removal of the Robinson et al. (2020) model residuals in the domain of the LFF statistic, on average. The variance of the corrected bias for each LFF statistic increased (Table 3, Column 8) compared with (Table 1, Column 7), with becoming larger with increasing T-year return period.
Inspection of Fig. 4 shows that application of the bias correction generally tended to lower the magnitude of the binned average bias values according to the plotting locations of the binned and values (red X and blue plus sign, respectively). For reference, the means reported in the top-margin box and whisker plot of Fig. 4 correspond to the computed and for each LFF statistic reported in Table 3.
The simulated LFF statistics that were initially overestimated relative to the corresponding gauged LFF statistics, generally values smaller than zero base-10 logarithm , were considerably less biased. Results for initially unbiased simulated LFF statistics were more varied (generally corresponding to gauged LFF statistics greater than or equal to zero). The slight underestimation seen initially in the uppermost bin ( base-10 logarithm bin) was appropriately mitigated for most LFF statistics; however, the bias correction tended to lower the simulated LFF statistic too much for some of the bins. For example, the simulated 30Q2 statistics corresponding to a gauged 30Q2 magnitude between and zero base-10 logarithm were overcorrected on average given the plotting location of the bias-corrected mean further away from the zero-bias line compared with the plotting location of the initial mean bias (Fig. 4). The overcorrection tended to increase with increasing T-year return period, but there was not an observable trend between the different N-day averaging periods. For the lowermost bins shown in Fig. 4, the bias-correction workflow appropriately lowered the bias, but there was still overestimation in the simulated LFF statistics given the location of the boxes and red X symbols left of the zero-bias line.
Uncertainty
The 95% prediction limits computed for the simulated LFF statistics [Eq. (11)] span about three orders of magnitude on average (Table 3, Column 7). Prediction limits were also computed for the stream gauges in the comparison data set using the same bootstrapping technique and assuming the statistical variance is the only source of uncertainty. The gauge 95% prediction limits, by comparison, only span between a quarter and half of a log-cycle, approximately (Table 3, Column 6). The width of the prediction limits for the gauge and simulated LFF statistics increased with increasing return period.
For all LFF statistics, standard error of fit was generally lowest in the interior and increased along the border of the study area (Fig. 7). The lowest gridded prediction estimate of GAM standard error occurred for the 7Q2, and the highest occurred for the 30Q20 (Table 3, Columns 3 and 4, respectively).
Discussion
Interpretation of Biases
Overestimation of simulated LFF statistics is interpreted heuristically to be caused by the ANN technique used by Worland et al. (2019a), which was not specifically tuned to the lower tail (extreme values as annual minima). Underestimation in the LFF statistics was observed as well, indicating that too much water was predicted for some HUC12s. This demonstrates a need for a correction scheme beyond one simply based on a constant , for example. Further, it was graphically shown that there were trends in the magnitude of the initial bias with the magnitude of the gauged LFF statistic (Fig. 4). The two-stage GAM fitting allows for flexibility in modeling the bias. With the goal in mind of leveraging the simulated streamflow for credible operational use, these characteristics are used to make choices about what is considered an unreliable simulated flow-frequency statistic and or help inform the decision for a GAM framework and details to follow.
As mentioned, with some knowledge of the characteristics of the initial biases, a specific GAM framework may be targeted to help improve bias-correction predictions where they are most needed. For example, bias corrections are most needed for the Robinson et al. (2020) simulated LFF statistics with a magnitude of about zero base-10 logarithm or less (Fig. 4). This may be stemming from the fact that the ANN was not apt for predicting low flows, and especially not zero flow (Worland et al. 2019a). The benefit of the two-stage GAM framework is that model-specific choices that drive the overestimation can potentially be mitigated by supplying additive terms to the Stage I GAM. Hence, we tested PET as an additive term because it was not incorporated in the ANN as an explanatory variable and it is positively correlated with no-flow (Zhao et al. 2022). The slight increase in explained deviance (Table 2, Column 1) compared with the simple GAM framework is thought to improve the bias predictions for the smaller magnitude LFF statistics that are less than zero base-10 logarithm .
Additionally, the ability to use different distribution families allows for some flexibility in dealing with nuanced data; infinite values of were handled using a censored normal distribution in both of the tested GAM frameworks. Computational issues arise if the GAM is fed extremely small values, which arose when the gauged LFF statistic was computed as , so the censoring allowed for these stream gauge-model differences to be somewhat honored instead of complete removal of the pairs.
Inherently, the shorter the N-day averaging period, the more likely the resultant gauged LFF statistic was to be computed as . Intuitively, one might expect overestimation to be larger for the 1-day LFF statistics because more frequent annual minima equal to are not being captured; however, the overestimation was largest for the 30-day statistics. This may be because overestimation was compounded as the N-day averaging period increased, a reflection of how the Worland et al. (2019a) modeling was optimized for daily mean flow as opposed to 30-day mean flow, or an artifact of decreasing noncensored sample size with decreasing N-day averaging period (sample size was obtained by subtracting Column 1 values in Table 1 from 497, the total number of stream gauge-model pairs).
The estimated spatial distribution of the Stage I GAM bias corrections is especially informative because it describes the nature of adjusting the simulated LFF estimates to an observational basis, but also because the spatial distribution informs practitioners that the Worland et al. (2019a) modeling increasingly seems to be overestimating streamflow in the lower hydrologic regimes, at least as expressed in the domain of the N-day averaging periods investigated. The latter is supported by the observation that the bias generally increased in magnitude (absolute value) toward the west into Texas (Fig. 5) as zero-flow frequency increased (Robinson et al. 2019 data files), and the simulated streamflow data were not optimal for frequent no-flow conditions. The prevalence of no-flow conditions increasingly toward the west was mimicked by the increase in stream gauge-model points having a gauged LFF statistic computed as because of a lack of nonzero flow in the gauged record (Fig. 5).
Underestimation of simulated LFF statistics constitutes a lesser portion of the values, but there was a consistent underestimation seen in the HUC12 watersheds located in the northern portion of Georgia for all LFF statistics (Fig. 5). The underestimation was different from that seen along the southern edge of the study area east of Texas and west of Florida (Fig. 5), which seems to be related to a paucity of stream gauges there (Figs. 1 and 7).
The location and extent of the underestimation in the northern portion of Georgia was coincident with an increase in the parameter-elevation relationships on independent slopes model (PRISM) 1971–2000 mean annual precipitation map relative to the surrounding area (Daly et al. 2008). Although Worland et al. (2019a) used the PRISM mean annual precipitation summarized by decade as an explanatory variable, they hypothesized that high streamflow driven by short duration precipitation events were not captured in their model output by the mean annual summaries. The underestimation seen in the northeast corner of Georgia is likely a residual effect from the lack of covariates that fully capture the hydrologic regime there.
Efficacy of the Proposed Workflow and Other Considerations
Application of the proposed two-stage GAM correction workflow to simulated LFF statistics mitigated the bias on average according to . The workflow applied to LFF statistics computed from simulated streamflow demonstrates that it is not feasible to use all initial, nor bias-corrected, simulated flow-frequency statistics for operational use. In general, LFF statistics cannot be reliably computed from Robinson et al. (2020) for streams that are ephemeral in nature, but streams that behave as perennial with predominantly nonzero streamflows appeared reliable. Investigating application of this workflow to other simulated streamflow data sets that are more apt for predicting no-flow could demonstrate whether operational use is justified for the ephemeral locations deemed unreliable here. In theory, the initial bias and variance of the derivative simulated flow-frequency statistic is zero when streamflow predictions are perfectly calibrated for predicting design flows in the tail of interest. In that case, the proposed bias-correction workflow may be entirely unnecessary. However, biases are expected because hydrologic models are not perfect, and this workflow allows for the biases to be identified in the specific domain of the desired flow-frequency statistic.
Although the magnitude of biases was effectively lowered on average, there are other aspects that need consideration when determining the efficacy of this workflow. First, what are acceptable prediction limits? When GAM uncertainty was accounted for in the practical application, the resulting prediction limits spanned between two and three orders of magnitude, which is quite wide. Interestingly, if we only considered the statistical variance as the source of uncertainty in the simulated LFF statistics, then prediction limits were narrower than the corresponding gauge on average. This indicates that GAM uncertainty dominates (Table 3, Column 8) and that variance reduction was present in the simulated LFF statistics, and this is also reflected in the initially small (Table 1, Column 7) values compared with the aforementioned GAM uncertainty (also the bias-corrected variance here). Second, is overcorrection a problem? Biases may be removed on average, but that does not imply success globally. In the context of the pour points coinciding with locations where LFF statistics have not been updated in several decades (Telis 1991), the demonstrated success of the workflow is highly advantageous.
Considering that several independently simulated FDCs showed underestimation of the high-flow regime (Fig. 1), application of this workflow to a high-flow frequency analysis would be extremely informative and could potentially expand operational use of simulated streamflows to flood-frequency statistics. Although not studied here, high-flow frequency bias corrections produced following the proposed workflow are expected to be predominantly positive, at least for the example HUC12 in Mississippi (Fig. 1). In addition, this workflow was tested on streamflow simulated from a data-driven hydrologic model, but the same workflow could be applied to outputs form other types of models, such as physically based models (Devia et al. 2015). Using this workflow as a framework for a comparative study could illuminate how model type plays a role in the characteristics of the bias when simulated streamflows are used to compute flow-frequency statistics.
The distributional range of the gauged flow-frequency statistics represented in the stream gauge-model pairs, as well as the spatial distribution of the pairs, needs to be considered when determining feasibility of simulated flow-frequency statistics. The latter is evidenced by the maps of the standard errors of fit of each LFF statistic (Fig. 7). The interior of the study area was characterized by decreased GAM standard errors for all LFF statistics. GAM standard errors tended to increase at the border of the study area also related to a paucity of stream gauges there, especially in southern Louisiana. It is important that the practitioner consider the range of magnitudes represented in the stream gauges used to model the bias. A specification of equal to is not suggested, for example, because it incorrectly implies that bias corrections are valid for any magnitude of a NQT statistic when in fact there is a finite range that is captured in the stream gauge-model pairs.
We suggest starting with a value of that honors censoring of unmeasured flow quantiles if such situations are not addressed in computation of the flow-frequency statistics in Step 4. For example, following the computation of LFF statistics proposed here would require that the lower threshold of be no less than base-10 logarithm , which approximates the lowest nonzero daily mean streamflow value reported by a USGS stream gauge.
Hypothetical Application of the Results to Operational Hydrology
In this section, the results pertaining to the simulated 7Q10 LFF statistic are discussed from the perspective of a hypothetical practitioner. Consider a practitioner that has decided the magnitude of biases shall not exceed a quarter of a log-cycle () in order to be considered as reliable for operational use. At a computed value of , the absolute value of exceeded the designated and indicates that the 7Q10 simulated LFF statistics need to be reduced by that magnitude on average (Table 1, Column 6). The values of are nonzero (Table 1, Column 7), and variation in the initial mean biases computed for all binned intervals of the gauge 7Q10 magnitude confirmed as much [Fig. 8(a)]. Following Step 6, the practitioner determines from the box and whisker plots [Fig. 8(a)] that ; notice how all binned mean initial biases in this range of the magnitude plotted within the to 0.25 () bias range.
Exclusion of the simulated 7Q10 statistics outside the range of resulted in a removal of nearly 75% of the HUC12 locations [Fig. 8(b), red points] with simulated streamflow. The remaining HUC12 pour points initially suitable for operational use occurred on mainstem rivers where observed streamflow records were likely available for conventional streamflow frequency analyses; therefore, the initially unbiased LFF statistics are presumably unhelpful to the practitioner. As such, a potential outcome of proceeding with the proposed workflow and computing 7Q10 bias corrections is that some of the unsuitable locations may be converted to suitable for operational use.
Application of the two-stage GAM correction workflow to the 7Q10 simulated LFF statistic mitigated the bias on average based on the value of (Table 3, Column 11), but there was variation in the corrected bias () with the magnitude of the corresponding gauged LFF statistic [Fig. 8(c)]. Some of the smallest magnitude simulated LFF statistics were still largely overestimated even with the bias correction applied, so the practitioner defines to determine the magnitude range of the bias-corrected simulated flow-frequency statistics that are considered as reliable for operational use based on the magnitude of .
Using the same as before, biases in the 7Q10 statistic were deemed inadequately bias-corrected for a corresponding gauged 7Q10 magnitude less than base-10 logarithm . Therefore, the lower bound of was . Above the lower bound, there were two unbiased ranges, where the LFF statistics within range one and two base-10 logarithm were biased and the uppermost bin was unbiased, according to the criteria and Fig. 8(c). The two uppermost bins were ignored for simplicity and there were not many stream gauges represented in the comparison data set with a 7Q10 magnitude greater than two anyway [Counts in Fig. 8(c)]. The upper bound for was then defined as one, and thus . Simulated 7Q10 estimates in the interval range of comprised 66% of the HUC12 locations [Fig. 8(d), red points].
Of the subset of reliable bias-corrected simulated 7Q10 statistics, the maximum (absolute value) of was four base-10 logarithm , applied to a value of 0.31 base-10 logarithm . In real-space, the uncorrected 7Q10 was about , and the bias-corrected 7Q10 evaluated to ; although the difference could be considered as small in real space by some, the computation emphasizes the importance of evaluating and conceptualizing the bias in log-space because the simulated 7Q10 may be biased by multiple orders of magnitude and nonnegative flow values are maintained in the correction scheme.
Having a comprehensive understanding of the characteristics of the initial and corrected bias in the 7Q10, the practitioner can credibly identify (un)reliable simulated flow-frequency statistics for operational use. When and overlap, the practitioner will need to decide if the initial or bias-corrected statistics are preferable. The central tendency statistics in the box and whisker plots are suggested to guide that decision, such as favoring the lower (absolute value) of the mean, median, or narrower interquartile range. Context may play an important role, too. For example, the bias correction overcorrected some of the 7Q10 statistics. The practitioner could favor underestimation to overestimation (up to some amount, of course) in the context of effluent discharge regulations and attendant permitting because more conservative estimates of low flow do not risk granting too much in relation to the real water availability (de Oliveira Serrano et al. 2020); therefore, the practitioner might favor the initially unbiased simulated 7Q10 estimates.
Regardless, the bias-correction workflow promoted the use of an additional 39% of HUC12 pour points suitable for operational use. Interestingly, the HUC12 locations deemed as reliable for operational use were similar to the locations with no-flow fractions estimated to be near zero (Crowley-Ornelas et al. 2017); this further supports the inference that overestimation is being driven by the inability of the ANN to predict zero flow values and provides an additional layer of comfort for the choice of specific to the 7Q10.
Conclusions
Derivative flow-frequency products of simulated streamflows are expected to be biased because of the complexities inherent to using simulated streamflow for flow-frequency analysis (Kirby 1975; Vogel 1999; Sivakumar 2005; Bourdin et al. 2012). The workflow described here for computing and evaluating biases in the realm of the desired flow frequency statistics is applicable to studies that seek to assess the feasibility of treating simulated streamflow as deterministic for operational use. The workflow involves fitting computed differences in flow-frequency statistics from stream gauge-model pairs to GAMs in a two-stage process. The efficacy of the workflow was examined by computing 12 LFF statistics from the simulated streamflow provided by Robinson et al. (2020) and comparing them with observations at several hundred common points in the southern and southeastern US.
Simulated LFF statistics were generally being overestimated by approximately a quarter to a half of a log-cycle, which demonstrated limited operational use of the simulated streamflow data set without addressing the biases. The results of this study showed that it is credibly feasible to compute LFF statistics for many of the HUC12 pour points (without a coincident stream gauge) after applying the spatial bias corrections. Using the simulated streamflow model output locations as the structural element to report and organize the flow-frequency statistics provides a comprehensive set of estimated statistics at ungauged locations where streamflow data are nonexistent. In conclusion, the workflow described here provides a powerful resource for practitioners interested in leveraging an ever-growing wealth of simulated streamflow data sets worldwide that water-resource managers may find extremely valuable.
Notation
The following symbols are used in this paper:
- cumulative drainage area for the stream gauge in units of length squared;
- cumulative drainage area for the ungauged (streamflow model output) location in units of length squared;
- difference between the simulated flow-frequency statistic with the total bias correction applied and gauged flow-frequency statistic, i.e., the corrected bias in base-10 logarithm units of streamflow;
- difference between the simulated and gauged flow-frequency statistic, i.e., the initial bias in units of base-10 logarithm units of streamflow;
- gauged flow-frequency statistic computed without any adjustments for stream gauge-model pair matching in units of base-10 logarithm units of streamflow;
- gauged flow-frequency statistic scaled to the ungauged (streamflow model output) location, in units of base-10 logarithm units of streamflow;
- simulated bias-corrected flow-frequency statistic in units of base-10 logarithm units of streamflow;
- simulated flow-frequency statistic in units of base-10 logarithm units of streamflow, without any bias correction;
- sum of the spatial bias correction () and the residual bias correction () from Stage I and II GAM fitting, respectively;
- N-day
- integer averaging period;
- number of stream gauge-model pairs or the number of ungauged modeling locations in the simulated streamflow data set; the former is applicable to the bias-computation and correction steps of this workflow; however, the later is only applicable to the final bias-correction step after the user completes the workflow evaluation step;
- T-year
- integer return period;
- interval range of the magnitude of gauged flow-frequency statistics, and simulated flow-frequency statistics by extension, considered to be unbiased and reliable for operational use that the user defines before () and or after () the application of the bias-correction workflow;
- cut-off value in terms of the magnitude of initial or corrected biases ( or , respectively) for designating how much bias the user considers to be too much and is equivalently expressed as an interval range of the cut-off value around a bias of zero base-10 logarithms of streamflow;
- statistical variance from the flow-frequency computations for an individual NQT statistic determined with a bootstrapping technique from Efron and Tibshirani (1985) in squared base-10 logarithm units of streamflow;
- variance of from a mean bias of zero in squared base-10 logarithm units of streamflow;
- variance stemming from the Stage I and II GAM predictions in squared base-10 logarithm units of streamflow;
- variance of from a mean bias of zero in squared base-10 logarithm units of streamflow; and
- exponent of unity used in the equations for estimating streamflow at an ungauged (streamflow model output) location following the DAR method (Hirsch 1979; Asquith et al. 2006).
Appendix I. Computation of LFF Statistics (Step 4)
The procedure to compute LFF statistics involved four major steps implemented by Whaling et al. (2022) and using functions from the lmomco package (Asquith 2023): (1) log-transformation of the series of N-day annual minima, (2) computation of L-moments, (3) parameter estimation for the PE3 distribution, and (4) extraction of the quantiles corresponding to the nonexceedance probabilities.
Two computational difficulties in the preceding procedure arose particularly when there was a dominance of zero flows in the annual minimum series. These difficulties were treated situationally and only existed for the gauged series because the ANN model inherently did not predict FDCs with zero [section “Robinson et al. (2020) Simulated Streamflow”]. The first difficulty occurred when there were fewer nonzero annual minima than the number of L-moments, minus one, needed to compute the parameters of the PE3 distribution. We computed the first four L-moments, so a degenerate series occurred when there were three or fewer nonzero annual minima. In such cases, the gauged LFF statistic could be treated as indeterminate, which ultimately removes the stream gauge-model pair from the analysis, or alternatively, as in log space because all of the values in real space are zero. The decision to enforce a value or exclude as indeterminable is made depending on the frequency of these situations within the stream gauge-model data set and the GAM frameworks tested in Step 7.
Recall that the purpose of the practical application of the workflow is to try to get a reasonably large sample size of gauged flow-frequency statistics from which to study simulated flow-frequency statistics and back into a correction that is regionalized. Correspondingly, we chose to enforce that the gauged LFF statistic be included as because a censored GAM framework was tested in Step 7 that somewhat incorporated the values into the bias modeling to increase the sample size of the stream gauge-model pairs. However, in other applications of this workflow, the simple option could be to treat the gauged LFF as indeterminable and remove the stream gauge-model pair from the analysis, granted the sample size is not severely reduced and or incorporation of the values in the GAM is not being attempted.
The second computational difficulty is related to the inability to log-transform the annual minima equaling zero. Although the initial log-transformation step mitigates extreme skewness in the data, the transformation results in values that cannot be directly used to compute the L-moments for estimation of the parameters of the PE3 distribution. For stream gauges with zero flows yet a sufficient amount of nonzero flows for parameter estimation, the gauged series was handled by a conditional probability adjustment before the log-transformation step with Weibull plotting positions, which are common in hydrology; a summary was provided by Asquith et al. (2017, Fig. 2-1), and described by England et al. (2019, p. 23) and Stedinger et al. (1993). Specifically, the Weibull plotting positions () were assigned to the series of annual minima, and the smallest of the nonzero annual minima was used as a truncation threshold in order to remap the full-range probability into the range within the noncensored part of the tail using the scaling operation in Eq. (13)where is a vector of nonexceedance probabilities; and = maximum plotting position of annual minima equal to zero (left-hand threshold). Effectively, the conditional probability adjustment will result in quantiles computed for nonexceedance probabilities that are lower than the truncation threshold to be computed as negative infinity () or zero log . To clarify, referenced in the scenario involving the truncation of the distribution by annual minima equal to zero is unrelated to the pp notation used in the aforementioned QppQ method to estimate ungauged streamflow at a location [section “Robinson et al. (2020) Simulated Streamflow”].
(13)
After accommodating the computational difficulties, L-moments were converted to parameters of the PE3 distribution. Following previous recommendations by Vogel and Fennessey (1993) and Kroll and Vogel (2002), we based our distribution choice partly on the location of the regional means of the L-moment ratio of the stream gauges on the L-moment ratio diagram of L-kurtosis versus L-skew (not provided here), and partly on historical precedence. The choice between three-parameter distribution families for this study is not of critical importance; the maximum depth into the distribution tail for this study is at the 20-year return period (0.05 nonexceedance probability) and other three-parameter distributions, such as the generalized extreme value and Weibull distributions, will produce quite similar results at the tail depths needed for this study (Asquith 2012). The final step in computing LFF statistics was to compute log-transformed quantiles for the nonexceedance probabilities. For example, from the 7-day annual minima, the 50th- and 10th-percentile annual low-flow quantiles, the 7Q2 and 7Q10, respectively, were computed from the fitted distribution.
Appendix II. Simple GAM Framework Results
Although all results following Steps 1–10 are documented in the companion software (Whaling et al. 2022), the primary results pertaining to the simple GAM framework [Eq. (6)] are reported in Table 4. The simple GAM framework uses a smooth on the spatial terms to investigate and correct for the spatial component of the bias at a minimum. The spatial distribution of the bias (Fig. 9) was similar to that seen by the compound GAM framework with overestimation of simulated LFF statistics dominating most of the study area, characterized by increasing magnitude moving west and southeast, and underestimation constituting a comparatively lesser portion of the study area that was greatest in the northeast (Fig. 10). Bias values near zero (unbiased) occurred in the east-central interior of the study area.
| LFF statistic | Mean | Mean | Minimum | Maximum | Mean | Mean gauge 95% PL width | Mean HUC12 95% PL width | Minimum | Maximum | |||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1Q2 | 0.40 | 1.02 | 0.26 | 2.47 | 0.40 | 1.89 | ||||||
| 1Q5 | 0.78 | 1.49 | 0.32 | 3.33 | 0.72 | 2.11 | ||||||
| 1Q10 | 1.00 | 1.79 | 0.40 | 3.94 | 1.01 | 2.59 | ||||||
| 1Q20 | 1.08 | 1.75 | 0.47 | 4.31 | 1.21 | 2.88 | ||||||
| 7Q2 | 0.30 | 0.69 | 0.27 | 2.42 | 0.38 | 1.87 | ||||||
| 7Q5 | 0.60 | 1.14 | 0.37 | 3.39 | 0.75 | 2.10 | ||||||
| 7Q10 | 0.85 | 1.47 | 0.41 | 3.79 | 0.93 | 2.53 | ||||||
| 7Q20 | 0.96 | 1.48 | 0.50 | 4.02 | 1.05 | 2.82 | ||||||
| 30Q2 | 0.12 | 0.39 | 0.31 | 2.42 | 0.38 | 1.82 | ||||||
| 30Q5 | 0.37 | 0.80 | 0.37 | 2.70 | 0.48 | 1.89 | ||||||
| 30Q10 | 0.51 | 1.04 | 0.49 | 3.57 | 0.83 | 2.30 | ||||||
| 30Q20 | 0.71 | 1.30 | 0.51 | 3.63 | 0.86 | 2.37 |
Note: Rows are labeled by LFF. The last data column contains values of for each LFF statistic from Table 1 to facilitate comparisons with . PL = prediction limit.
Data Availability Statement
Code used to generate all results, tables, and figures referenced herein are available in a companion software publication (Whaling et al. 2022) at https://code.usgs.gov/water/restore/syntheticdv2lff (tagged version 2.0.0).
Acknowledgments
Funding for this research was provided by the Gulf Coast Ecosystem Restoration Council (RESTORE 2016). We would like to thank Lucas Driver, hydrologist for the US Geological Survey, for his thorough peer review of the manuscript, and the anonymous journal reviewers for their constructive feedback.
Disclaimer
Any use of trade, firm, or product names is for descriptive purposes only and does not imply endorsement by the US Government.
References
Akaike, H. 1974. “A new look at the statistical model identification.” IEEE Trans. Autom. Control 19 (6): 716–723. https://doi.org/10.1109/TAC.1974.1100705.
Asquith, W. H. 2012. Distributional analysis with L-moment statistics using the R environment for statistical computing. Scotts Valley, CA: Createspace.
Asquith, W. H. 2020. “RESTORE/fdclmrpplo—Source code for estimation of L-moments and percent no-flow conditions for decadal flow-duration curves and estimation at level-12 hydrologic unit codes along with other statistical computations.” Accessed August 16, 2023. https://code.usgs.gov/water/restore/fdclmrpplo.
Asquith, W. H. 2023. “lmomco—L-moments, censored L-moments, trimmed L-moments, L-comoments, and many distributions.” Accessed September 4, 2023. https://cran.r-project.org/web/packages/lmomco/index.html.
Asquith, W. H., J. E. Kiang, and T. A. Cohn. 2017. Application of at-site peak-streamflow frequency analyses for very low annual exceedance probabilities. Reston, VA: USGS. https://doi.org/10.3133/sir20175038.
Asquith, W. H., M. C. Roussel, and J. Vrabel. 2006. Statewide analysis of the drainage-area ratio method for 34 streamflow percentile ranges in Texas. Reston, VA: USGS.
Asquith, W. H., and D. B. Thompson. 2008. Alternative regression equations for estimation of annual peak-streamflow frequency for undeveloped watersheds in Texas using press minimization. Reston, VA: USGS.
Becker, R. A., and A. R. Wilks. 2022. “maps: Draw geographical maps—R version by Ray Brownrigg. Enhancements by Thomas P. Minka and Alex Deckmyn.” Accessed September 4, 2023. https://CRAN.R-project.org/package=maps.
Blum, A. G., S. A. Archfield, R. M. Hirsch, R. M. Vogel, J. E. Kiang, and R. W. Dudley. 2019. “Updating estimates of low-streamflow statistics to account for possible trends.” Hydrol. Sci. J. 64 (12): 1404–1414. https://doi.org/10.1080/02626667.2019.1655148.
Bourdin, D. R., S. W. Fleming, and R. B. Stull. 2012. “Streamflow modelling: A primer on applications, approaches and challenges.” Atmos. Ocean 50 (4): 507–536. https://doi.org/10.1080/07055900.2012.734276.
Brooks, B. W., T. M. Riley, and R. D. Taylor. 2006. “Water quality of effluent-dominated ecosystems: Ecotoxicological, hydrological, and management considerations.” Hydrobiologia 556 (1): 365–379. https://doi.org/10.1007/s10750-004-0189-7.
Chambers, J. M., W. S. Cleveland, B. Kleiner, and P. A. Tukey. 1983. Graphical methods for data analysis. New York: Chapman and Hall.
Clark, B. R., P. M. Barlow, S. M. Peterson, J. D. Hughes, H. W. Reeves, and R. J. Viger. 2018. “National-scale grid to support regional groundwater availability studies and a national hydrogeologic database.” Accessed July 5, 2020. https://www.sciencebase.gov/catalog/item/5a95dd5de4b06990606a805e.
Crowley-Ornelas, E., W. H. Asquith, and S. C. Worland. 2017. Generalized additive model estimation of no-flow fractions and L-moments to support flow-duration curve quantile estimation using selected probability distributions for bay and estuary restoration in the Gulf States. Reston, VA: USGS.
Crowley-Ornelas, E. R., R. R. Knight, S. C. Worland, and W. H. Asquith. 2019. “Heuristically-determined geospatial boundary of streams and rivers draining to the Gulf of Mexico in south-central to southeastern United States, July 2018.” Accessed July 5, 2020. https://www.sciencebase.gov/catalog/item/5b5b30fde4b006a11f63f3b1.
Daly, C., M. Halbleib, J. Smith, W. Gibson, M. Doggett, G. Taylor, J. Curtis, and P. Pasteris. 2008. “Physiographically sensitive mapping of climatological temperature and precipitation across the conterminous United States.” Int. J. Climatol. 28 (15): 2031–2064. https://doi.org/10.1002/joc.1688.
De Cicco, L. A., D. Lorenz, R. M. Hirsch, and W. Watkins. 2022. “dataRetrieval—R packages for discovering and retrieving water data available from U.S. federal hydrologic web services.” Accessed August 2, 2022. https://code.usgs.gov/water/dataRetrieval.
de Oliveira Serrano, L., R. B. Ribeiro, A. C. Borges, and F. F. Pruski. 2020. “Low-flow seasonality and effects on water availability throughout the river network.” Water Resour. Manage. 34 (4): 1289–1304. https://doi.org/10.1007/s11269-020-02499-3.
Devia, G. K., B. Ganasri, and G. Dwarakish. 2015. “A review on hydrological models.” Aquat. Procedia 4 (Jan): 1001–1007. https://doi.org/10.1016/j.aqpro.2015.02.126.
Dey, D., D. Roy, and J. Yan. 2016. Univariate extreme value analysis. New York: Chapman and Hall.
Dudley, R., R. Hirsch, S. Archfield, A. Blum, and B. Renard. 2020. “Low streamflow trends at human-impacted and reference basins in the United States.” J. Hydrol. 580 (Jan): 124254. https://doi.org/10.1016/j.jhydrol.2019.124254.
Efron, B., and R. Tibshirani. 1985. “The bootstrap method for assessing statistical accuracy.” Behaviormetrika 12 (17): 1–35. https://doi.org/10.2333/bhmk.12.17_1.
England, J. F., T. A. Cohn, B. A. Faber, J. R. Stedinger, W. O. Thomas, A. G. Veilleux, J. E. Kiang, and R. R. Mason. 2019. “Guidelines for determining flood flow frequency—bulletin 17c.” In US Geological Survey techniques and methods. Reston, VA: USGS.
Farmer, W., and R. Vogel. 2016. “On the deterministic and stochastic use of hydrologic models.” Water Resour. Res. 52 (7): 5619–5633. https://doi.org/10.1002/2016WR019129.
Farmer, W. H., T. M. Over, and J. E. Kiang. 2018. “Bias correction of simulated historical daily streamflow at ungauged locations by using independently estimated flow duration curves.” Hydrol. Earth Syst. Sci. 22 (11): 5741–5758. https://doi.org/10.5194/hess-22-5741-2018.
Feaster, T. D., K. R. Kolb, J. A. Painter, and J. M. Clark. 2020. Methods for estimating selected low-flow frequency statistics and mean annual flow for ungaged locations on streams in Alabama. Reston, VA: USGS.
Fennessey, N. M. 1994. “A hydro-climatological model of daily streamflow for the northeast United States.” Ph.D. thesis, Dept. of Civil and Environmental Engineering, Tufts Univ.
Floriancic, M. G., W. R. Berghuijs, P. Molnar, and J. W. Kirchner. 2021. “Seasonality and drivers of low flows across Europe and the united states.” Water Resour. Res. 57 (9): e2019WR026928. https://doi.org/10.1029/2019WR026928.
Funkhouser, J. E., K. Eng, and M. W. Moix. 2008. Low-flow characteristics and regionalization of low-flow characteristics for selected streams in Arkansas. Reston, VA: USGS.
Good, P. I., and J. W. Hardin. 2012. Common errors in statistics (and how to avoid them). Hoboken, NJ: Wiley.
Gotvald, A. J. 2016. Selected low-flow frequency statistics for continuous-record streamgages in Georgia, 2013. Reston, VA: USGS.
Guo, J., J. Zhou, J. Lu, Q. Zou, H. Zhang, and S. Bi. 2014. “Multi-objective optimization of empirical hydrological model for streamflow prediction.” J. Hydrol. 511 (Apr): 242–253. https://doi.org/10.1016/j.jhydrol.2014.01.047.
Hammett, K. 1985. Low-flow frequency analyses for streams in west-central Florida. Reston, VA: USGS.
Hirsch, R. M. 1979. “An evaluation of some record reconstruction techniques.” Water Resour. Res. 15 (6): 1781–1790. https://doi.org/10.1029/WR015i006p01781.
Horton, P., B. Schaefli, and M. Kauzlaric. 2022. “Why do we have so many different hydrological models? A review based on the case of Switzerland.” WIREs Water 9 (1): e1574. https://doi.org/10.1002/wat2.1574.
Huntzinger, T. L. 1978. Low-flow characteristics of Oklahoma streams. Reston, VA: USGS.
Kim, T., T. Yang, S. Gao, L. Zhang, Z. Ding, X. Wen, J. J. Gourley, and Y. Hong. 2021. “Can artificial intelligence and data-driven machine learning models match or even replace process-driven hydrologic models for streamflow simulation? A case study of four watersheds with different hydro-climatic regions across the CONUS.” J. Hydrol. 598 (Jul): 126423. https://doi.org/10.1016/j.jhydrol.2021.126423.
Kirby, W. 1975. “Model smoothing effect diminishes simulated flood peak variance.” Am. Geophys. Union Trans. 56 (6): 361.
Kroll, C. N., and R. M. Vogel. 2002. “Probability distribution of low streamflow series in the united states.” J. Hydrol. Eng. 7 (2): 137–146. https://doi.org/10.1061/(ASCE)1084-0699(2002)7:2(137).
Law, G. S., G. D. Tasker, and D. E. Ladd. 2009. Streamflow-characteristic estimation methods for unregulated streams of Tennessee. Reston, VA: USGS.
Lorenz, D. 2017. USGS-R/DVstats—Functions to manipulate daily-values data. Reston, VA: USGS.
Markstrom, S. L., L. E. Hay, and M. P. Clark. 2016. “Towards simplification of hydrologic modeling: Identification of dominant processes.” Hydrol. Earth Syst. Sci. 20 (11): 4655–4671. https://doi.org/10.5194/hess-20-4655-2016.
Martin, G. R., and L. D. Arihood. 2010. Methods for estimating selected low-flow frequency statistics for unregulated streams in Kentucky. Reston, VA: USGS.
McKay, L., T. Bondelid, T. Dewald, C. M. Johnston, R. B. Moore, and A. Rea. 2016. “National Hydrography dataset (NHD) plus version 2.1, 1:100,000-scale.” Accessed July 5, 2020. http://horizon-systems.com/NHDPlus/.
Murphy, J. C., R. R. Knight, W. J. Wolfe, and W. S. Gain. 2013. “Predicting ecological flow regime at ungaged sites: A comparison of methods.” River Res. Appl. 29 (5): 660–669. https://doi.org/10.1002/rra.2570.
Nelson, R. B. 2006. Vol. 6 of An introduction to copulas. New York: Springer.
NOAA (National Oceanic and Atmospheric Administration) and National Centers for Environmental Information. 2023. “nclimgrid gridded drought indices [pet].” Accessed April 17, 2023. https://www.ncei.noaa.gov/pub/data/nidis/indices/nclimgrid-monthly/pet/.
R Core Team. 2022. R: A language and environment for statistical computing. Vienna, Austria: R Core Team.
Reilly, C. F., and C. N. Kroll. 2003. “Estimation of 7-day, 10-year low-streamflow statistics using baseflow correlation.” Water Resour. Res. 39 (9): 1236. https://doi.org/10.1029/2002WR001740.
RESTORE (Gulf Coast Ecosystem Restoration Council). 2016. “Gulf coast ecosystem restoration council comprehensive plan—Approved comprehensive plan update 2016.” Accessed September 4, 2023. https://www.restorethegulf.gov/.
Ritter, A., and R. Muñoz-Carpena. 2013. “Performance evaluation of hydrological models: Statistical significance for reducing subjectivity in goodness-of-fit assessments.” J. Hydrol. 480 (Feb): 33–45. https://doi.org/10.1016/j.jhydrol.2012.12.004.
Robinson, A. L., W. H. Asquith, and R. R. Knight. 2019. “Summary of decadal no-flow fractions and decadal L-moments of nonzero streamflow flow-duration curves for National hydrography dataset, version 2 catchments in the southeastern United States, 1950–2010.” Accessed July 5, 2020. https://www.sciencebase.gov/catalog/item/5cc1b692e4b09b8c0b746dc9.
Robinson, A. L., S. C. Worland, and K. D. Rodgers. 2020. “Estimated daily mean streamflows for HUC12 pour points in the southeastern United States, 1950–2009.” Accessed July 5, 2020. https://www.sciencebase.gov/catalog/item/5d43175be4b01d82ce8db055.
Rodgers, K. D., V. Roland, A. Hoos, E. R. Crowley-Ornelas, and R. R. Knight. 2020. “An analysis of streamflow trends in the southern and southeastern US from 1950–2015.” Water 12 (12): 3345. https://doi.org/10.3390/w12123345.
Russell, A., T. Over, W. Farmer, and K. Miles. 2021. “Statistical daily streamflow estimates at GAGES-II non-reference streamgages in the conterminous United States, water years 1981–2017.” Accessed April 3, 2023. https://www.sciencebase.gov/catalog/item/5efb512e82ced62aaaf057fe.
Scott, D. W. 2009. “Sturges’ rule.” Wiley Interdiscip. Rev. Comput. Stat. 1 (3): 303–306. https://doi.org/10.1002/wics.35.
Searcy, J. K. 1959. Flow-duration curves. Reston, VA: USGS.
Sivakumar, B. 2005. “Hydrologic modeling and forecasting: Role of thresholds.” Environ. Modell. Software 20 (5): 515–519. https://doi.org/10.1016/j.envsoft.2004.08.006.
Smakhtin, V. 2001. “Low flow hydrology: A review.” J. Hydrol. 240 (3): 147–186. https://doi.org/10.1016/S0022-1694(00)00340-1.
Southard, R. E. 2013. Computed statistics at streamgages, and methods for estimating low-flow frequency statistics and development of regional regression equations for estimating low-flow frequency statistics at ungaged locations in Missouri. Reston, VA: USGS.
Stedinger, J. R., R. M. Vogel, and E. Foufoula-Georgiou. 1993. Frequency analysis of extreme events.” Chap. 18 in Handbook of hydrology, edited by D. A. Maidment. New York: McGraw-Hill.
Stephens, T. A., and B. P. Bledsoe. 2020. “Low-flow trends at southeast united states streamflow gauges.” J. Water Resour. Plann. Manage. 146 (6): 04020032. https://doi.org/10.1061/(ASCE)WR.1943-5452.0001212.
Telis, P. A. 1991. Low-flow and flow-duration characteristics of Mississippi streams. Reston, VA: USGS.
USGS. 2023. “National water information system data available on the world wide web (USGS water data for the nation).” Accessed April 14, 2023. http://waterdata.usgs.gov/nwis/.
Vogel, R. M. 1999. “Editorial.” J. Water Resour. Plann. Manage. 125 (6): 311–313. https://doi.org/10.1061/(ASCE)0733-9496(1999)125:6(311).
Vogel, R. M., and N. M. Fennessey. 1993. “L moment diagrams should replace product moment diagrams.” Water Resour. Res. 29 (6): 1745–1752. https://doi.org/10.1029/93WR00341.
Wasko, C., S. Westra, R. Nathan, H. G. Orr, G. Villarini, R. Villalobos Herrera, and H. J. Fowler. 2021. “Incorporating climate change in flood estimation guidance.” Philos. Trans. R. Soc. London, Ser. A 379 (2195): 20190548. https://doi.org/10.1098/rsta.2019.0548.
Whaling, A. R., K. M. Sanks, and W. H. Asquith. 2022. “RESTORE/syntheticdv2lff—Scripts for low-streamflow (low-flow) frequency (LFF) estimation from synthetic daily mean streamflow with bias correction estimated at perennial level-12 hydrologic unit code (HUC12) pour points in the south-central and southeastern United States.” Accessed September 4, 2023. https://code.usgs.gov/water/restore/syntheticdv2lff.
Wood, S. N. 2003. “Thin plate regression splines.” J. R. Stat. Soc.: Ser. B 65 (1): 95–114. https://doi.org/10.1111/1467-9868.00374.
Wood, S. N. 2011. “Fast stable restricted maximum likelihood and marginal likelihood estimation of semiparametric generalized linear models.” J. R. Stat. Soc.: Ser. B 73 (1): 3–36. https://doi.org/10.1111/j.1467-9868.2010.00749.x.
Wood, S. N. 2020. “Inference and computation with generalized additive models and their extensions.” Test 29 (2): 307–339. https://doi.org/10.1007/s11749-020-00711-5.
Wood, S. N. 2021. “mgcv—Mixed GAM computation vehicle with automatic smoothness estimation.” https://cran.r-project.org/web/packages/mgcv/mgcv.pdf.
Worland, S. C., S. Steinschneider, W. H. Asquith, R. R. Knight, and M. E. Wieczorek. 2019a. “Prediction and inference of flow duration curves using multioutput neural networks.” Water Resour. Res. 55 (8): 6850–6868. https://doi.org/10.1029/2018WR024463.
Worland, S. C., S. Steinschneider, W. Farmer, W. H. Asquith, and R. R. Knight. 2019b. “Copula theory as a generalized framework for flow-duration curve based streamflow estimates in ungaged and partially gaged catchments.” Water Resour. Res. 55 (11): 9378–9397. https://doi.org/10.1029/2019WR025138.
Wright, L. S., and P. A. Ensminger. 2004. Regionalized regression equations for estimating low-flow characteristics for selected Louisiana streams. Baton Rouge, LA: Louisiana DOT and Development.
Zhang, Y., F. H. S. Chiew, M. Li, and D. Post. 2018. “Predicting runoff signatures using regression and hydrological modeling approaches.” Water Resour. Res. 54 (10): 7859–7878. https://doi.org/10.1029/2018WR023325.
Zhao, M., Y. Liu, and A. G. Konings. 2022. “Evapotranspiration frequently increases during droughts.” Nat. Clim. Change 12 (11): 1024–1030. https://doi.org/10.1038/s41558-022-01505-3.
Information & Authors
Information
Published In
Journal of Hydrologic Engineering
Volume 29 • Issue 5 • October 2024
Copyright
This work is made available under the terms of the Creative Commons Attribution 4.0 International license, https://creativecommons.org/licenses/by/4.0/.
History
Received: Oct 24, 2022
Accepted: Feb 13, 2024
Published online: Jul 1, 2024
Published in print: Oct 1, 2024
Discussion open until: Dec 1, 2024
ASCE Technical Topics:
- Analysis (by type)
- Computer models
- Engineering fundamentals
- Flow (fluid dynamics)
- Fluid dynamics
- Fluid mechanics
- Frequency analysis
- Hydrologic engineering
- Hydrologic models
- Mathematics
- Models (by type)
- River and stream beds
- River engineering
- Rivers and streams
- Simulation models
- Statistics
- Stream gauge
- Streamflow
- Water and water resources
Authors
Metrics & Citations
Metrics
Citations
Download citation
If you have the appropriate software installed, you can download article citation data to the citation manager of your choice. Simply select your manager software from the list below and click Download.