Unified Modeling for the Simple Shear Behavior of Clay and Sand Accounting for Principal Stress Rotations

Yuan, Ran; Yu, Hai-Hong; Wang, Xiao-Wen

doi:10.1061/IJGNAI.GMENG-8399

Open access

Technical Papers

Aug 20, 2024

Unified Modeling for the Simple Shear Behavior of Clay and Sand Accounting for Principal Stress Rotations

Authors: Ran Yuan https://orcid.org/0000-0001-6620-6587 [email protected], Hai-Hong Yu [email protected], and Xiao-Wen Wang https://orcid.org/0000-0002-0543-2537 [email protected]Author Affiliations

Publication: International Journal of Geomechanics

Volume 24, Issue 11

https://doi.org/10.1061/IJGNAI.GMENG-8399

PDF

Abstract

Mechanical response of soils under simple shear conditions has long been a subject of significant interest in the field of geomechanics. When subjected to simple shear loading, soils experience rotations of the principal stress directions. To provide a unified description for the simple shear behavior of clay and sand, this paper proposes a novel critical state model that accounts for the influence of principal stress rotation (PSR), based on the unified critical state model for overconsolidated clay and sand with subloading surface (CASM-S). The novelty of the newly proposed model, which is named as CASM-SP, lies in its ability to consider the influence of direction of the stress increment when establishing the plastic flow rule that is suitable for both clay and sand. Therefore, the model can capture the mechanical response of soils resulting from the PSR loading mechanism, such as noncoaxial behaviors. Then, the newly proposed model is validated through the comparisons with a series of experimental data of clay and sand under both drained and undrained simple shear conditions. Results predicted by the CASM-SP model agree well with those from the experiments, demonstrating that CASM-SP can reasonably describe the simple shear behavior of both clay and sand.

Introduction

Simple shear deformation is commonly observed in practical engineering applications. For instance, the soil in localized failure zones primarily undergoes simple shear deformation. In fact, as pointed out by Frydman and Talesnick (1991), simple shear deformation exists along the slip surface in any plane strain problem. Therefore, investigating the mechanical characteristics of soils under simple shear conditions has always been an important research topic in geotechnical engineering (Li et al. 2017; Pradhan et al. 1988; Thornton and Zhang 2006; Wang et al. 2023a; Wu et al. 2020; Yang et al. 2021).

Numerous studies have revealed that soils undergo principal stress rotation (PSR) under simple shear conditions (Pradhan et al. 1988; Yoshimine et al. 1999). Due to principal stress rotations, the direction of principal stress typically does not coincide with that of principal strain (or plastic principal strain) increment during the initial stages of the loading process, a phenomenon referred to as noncoaxial behavior (Chen and Huang 2020; Gao and Zhao 2017; Gutierrez and Ishihara 2000; Houlsby et al. 2019; Lashkari and Latifi 2008; Li and Dafalias 2020; Shen et al. 2022; Yuan et al. 2018b, 2019b). When modeling the simple shear behavior of soil using traditional elastoplastic theory, it is commonly assumed that plastic deformation is solely induced by a change of magnitude in the principal stress, without considering the effect of change in the stress direction. Taking the example of pure PSR loading, where the magnitude of principal stress remains constant while the direction changes continuously, the traditional elastoplastic theory treats such loading as neutral loading and predicts pure elastic behavior. However, significant plastic deformation has been observed in the pure PSR experiments of both clay and sand (Chen et al. 2021; Miura et al. 1986; Qian et al. 2018; Wang et al. 2019b; Yoshimine et al. 1998). Furthermore, as identified by Yang and Yu (2006a, 2010) and Yuan et al. (2018a, 2018b, 2019b) through a series of numerical simulations, neglecting the influence of noncoaxial behavior when modeling mechanical characteristics of soils may result in an unrealistic prediction of soil strength.

To accurately describe the mechanical characteristics of soils under simple shear conditions, numerous frameworks of constitutive modeling have been proposed. Rudnicki and Rice (1975) first proposed the yield vertex tangential loading theory as a supplement to traditional elastoplastic theory. Building upon this, Hashiguchi and Tsutsumi (2001, 2003) modified the traditional elastoplastic theory by incorporating the influence of the stress rate component tangential to the yield surface. The introduction of this theory makes it possible for constitutive models to consider the plastic deformation induced by the changing of principal stress directions. After that, Yang and Yu (2006a, 2006b), Qian et al. (2008), Yuan et al. (2018a, 2019b), and Du et al. (2022) have proposed a series of constitutive models under the framework of yield vertex tangential loading theory to make a reasonable prediction of soils under simple shear loading. While these models have achieved significant success in simulating the noncoaxial behavior of soils, as pointed out by Lu et al. (2019), the contributions of principal stress rotation and Lode angle in the yield vertex tangential loading theory may not be clear. To specifically account for the influence of principal stress rotations, Gutierrez et al. (1991, 1993, 2009) proposed a modified plastic flow rule to characterize the stress increment direction dependency of plastic flow. Within this framework, the plastic flow is decomposed into coaxial and noncoaxial parts. Based on the noncoaxial plastic flow rule, Lashkari and Latifi (2008) introduced the concept of fabric anisotropy into the noncoaxial plastic flow rule to explain the anisotropic behavior of sand under PSR. Lu et al. (2020) presented a new Cam-clay type model designed to effectively capture the effect of PSR on the simple shear response of clay. In addition to the constitutive models based on phenomenological approaches mentioned previously, there is a significant portion of models that incorporate microstructural information such as the fabric tensor. These models aim to explain the mechanical characteristics of soil under PSR conditions by considering the evolution of the fabric tensor (Cui et al. 2024; Li and Dafalias 2012; Liao and Yang 2022; Tian and Yao 2018; Wang et al. 2021; Xue et al. 2021; Yao et al. 2017; Yu et al. 2022; Yuan et al. 2019a). However, this approach requires accurate quantification of the initial fabric tensor and its evolution during the loading process. Although constitutive models incorporating the fabric tensor have the advantage of modeling microstructural information of soils, there has always been interest in the field of geotechnical engineering applications for a simple and balanced constitutive model to be developed to well capture both the mechanical behaviors of sand and clay through the phenomenological approach, and examples can be found, such as the reports by Yu et al. (2019) and Mo et al. (2021). However, these models are developed irrespective of PSR effects induced by simple shear loading.

Therefore, the objective of this paper is to develop a simple unified model to describe simple shear responses of clay and sand, and that considers the effect of PSR loading. This novel model, named as CASM-SP, is developed based on the CASM-S model (Cui et al. 2023; Wang et al. 2023b). The yield surface of CASM-SP is the same as the unified yield surface proposed by Yu (1998) for both sand and clay, and assumes the presence of a subloading surface (Hashiguchi 1989, 2022; Tsutsumi et al. 2006) inside the yield surface. This approach ensures that CASM-SP can characterize elastoplastic behavior within the yield surface. Then, CASM-SP introduces an additional PSR plastic flow mechanism defined by Lu et al. (2019, 2020), which allows the model to account for the effect of PSR on the simple shear response of both clay and sand. Finally, the newly proposed model is validated by comparisons between the simulation results of CASM-SP and experimental data from a series of simple shear tests for drained and undrained clay and sand.

Constitutive Relation of CASM-SP: Development and Implementation

This study follows the convention where compression of soil is denoted positive. The stress discussed here is considered as an effective stress. In algebraic terms, the following symbols and tensor operations are defined:

δ = δ_{i j}

(Kronecker delta tensor),

I = I_{i j k l} = (δ_{i k} δ_{i j} + δ_{i l} δ_{i k}) / 2

,

a : b = a_{i j} b_{i j}

,

a \otimes b = a_{i j} b_{k l}

,

t r (a) = a_{i i}

, and

‖ a ‖ = \sqrt{a_{i j} a_{i j}}

.

Critical State Theory, a Brief Review

The critical state of a soil is a well-known concept (Schofield and Wroth 1968), and it refers to the state where the soil continuously deforms under shear at constant volume and constant stress. The critical state is commonly defined as

d p = 0, d s = 0, d ε_{v} = t r (d ε) = 0

(1)

p = t r (σ) / 3, s = σ - p δ

(2)

where p = mean stress;

σ

= stress tensor;

s

= deviatoric stress tensor; and

d ε

and

d ε_{v}

= total and volumetric strain increments, respectively. Based on the unique characteristics exhibited by the soil under the critical state, the following equations can be defined in the e – p – q space:

\frac{q}{p} = η = M, q = \sqrt{\frac{3}{2}} ‖ s ‖

(3)

e = e_{Γ} - λ \ln p

(4)

where q = deviatoric stress; η = stress ratio; e = void ratio;

e_{Γ}

= intersection of the critical state line (CSL) with p = 1 kPa line in e–ln p space; and M = the slope of CSL in the p–q plane. As in Fig. 1, λ = the slope of CSL in e–lnp space. It should be noted that the CSL within the e–lnp space might exhibit nonlinearity due to particle breakage at higher pressures (Been et al. 1991). Under such circumstances, the correlation between e and lnp is better represented by either a bilinear or a nonlinear relationship (Li and Wang 1998; Yin et al. 2018). For the sake of simplicity, this study disregards the influence of particle breakage. Hence, the linear relationship between e and lnp as defined in Eq. (4) is adopted in this study. This is a reasonable simplification that has been demonstrated by the previous research (e.g., Yu 1998).

Fig. 1. Definitions of critical state line (CSL), reference consolidation line (RCL), and swelling line (SL) in the v–ln p plane based on Yu (1998).

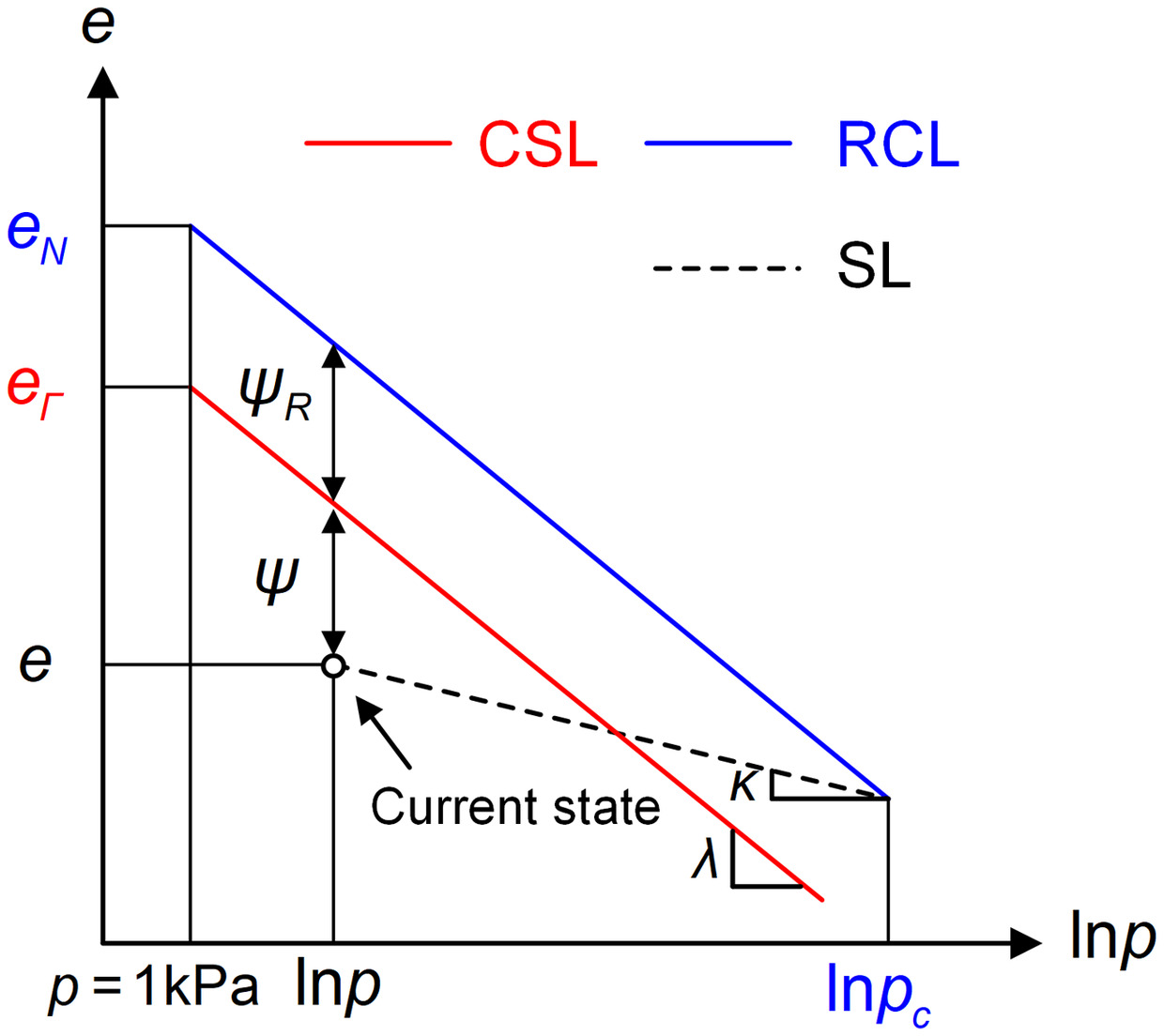
As in Fig. 1, to relax the original kinematical hypothesis of the critical state theory to characterize the mechanical properties of sand, Been et al. (1991), Jefferies (1993), and Yu (1998) introduced the theory of state parameter and reference state parameter. These parameters can be given as follows:

ψ = e + λ \ln p - e_{Γ}

(5)

ψ_{R} = (λ - κ) \ln r

(6)

where ψ = state parameter, which equals to zero at the critical state; however, it is positive on the “wet” side and negative on the “dry” side; ψ_R = reference state parameter; r = spacing ratio employed to estimate the reference state parameter and corresponds to the loosest state attainable by the soil in practical conditions; and κ = slope of the swelling line (SL) in the e–lnp space.

Yield Criterion and Subloading Function of CASM-SP

Drawing from the critical state theory and concept of state parameters, Yu (1998) introduced a unified critical state model known as the clay and sand model (CASM). This model encompasses the behavior of both clay and sand. Due to its straightforward nature and broad applicability, the CASM model has gained widespread adoption and has been further refined to address practical engineering challenges (Khong 2004; Rios et al. 2012). Nevertheless, as highlighted by Hashiguchi et al. (2002), the conventional elastoplastic theory used in models such as CASM relies on the assumption that the interior of the yield surface represents a purely elastic region. While this assumption does not result in impractical forecasts of hardening behavior, it does yield unrealistic predictions of softening behavior, which is frequently observed in overconsolidated clays and dense sands.

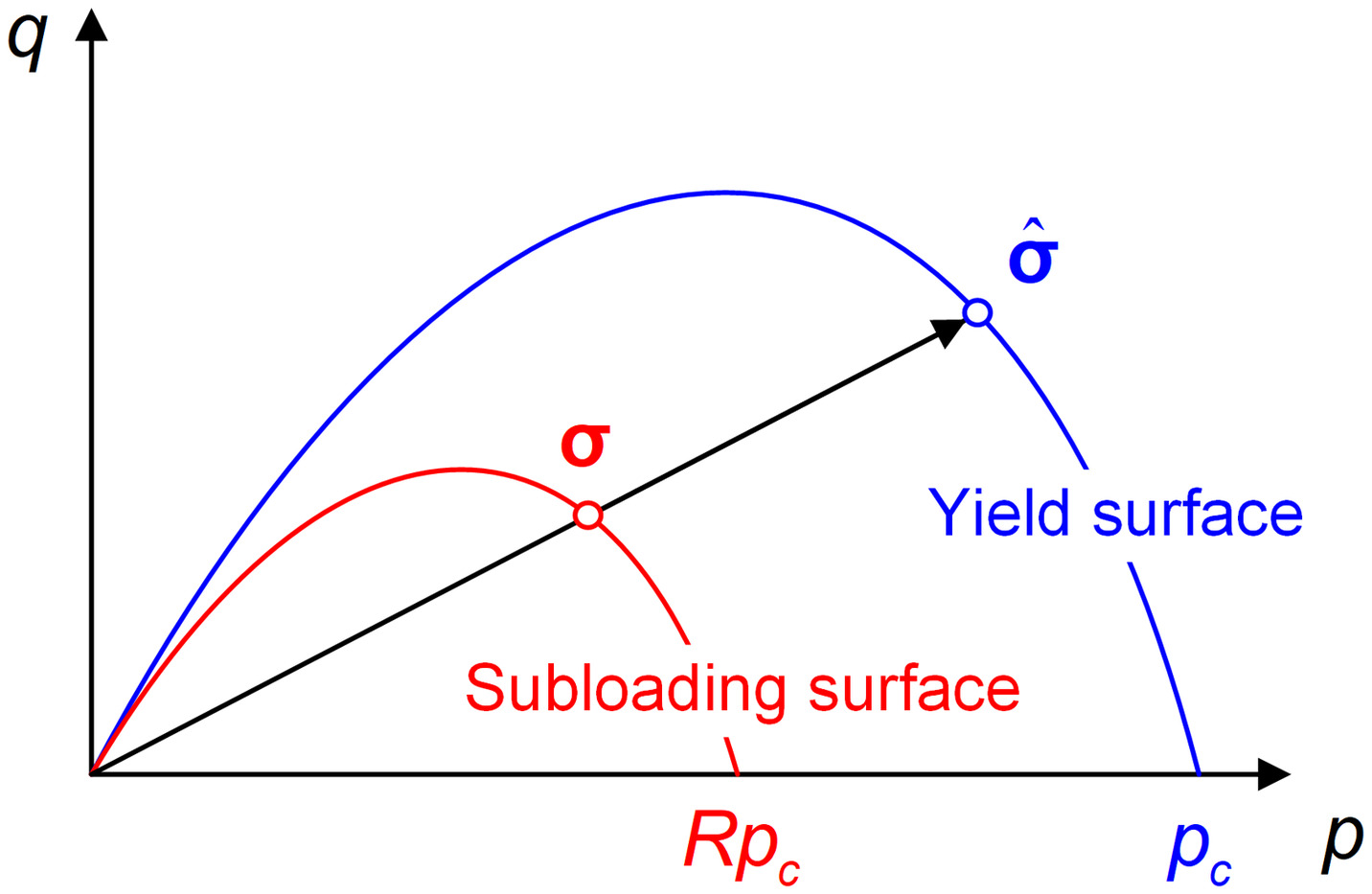
Therefore, Cui et al. (2023) introduced the subloading surface theory into the original CASM model and proposed the CASM-S model. The CASM-S model introduced a subloading surface determined by the current stress state into the yield surface of the original CASM model. The shape of the subloading surface is similar to the yield surface at all times. Likewise, in this study, it is assumed that the yield surface of CASM-SP is consistent with that of CASM, and there is a subloading surface in the yield surface, as depicted in Fig. 2. The stress state on the subloading surface and the conjugate stress on the yield surface satisfy the following relationship:

\hat{p} = p / R, \hat{q} = q / R

(7)

where

\hat{σ}

(

\hat{p}

,

\hat{q}

) = conjugate stress of

σ

on the yield surface; and R = size ratio of subloading surface to yield surface. Therefore, the subloading surface f and yield surface

\hat{f}

of CASM-SP can be defined as

\hat{f} = {(\frac{\hat{q}}{M \hat{p}})}^{n} + \frac{\ln (\hat{p} / p_{c})}{\ln r}

(8)

f = {(\frac{q}{M p})}^{n} + \frac{\ln (p / R p_{c})}{\ln r}

(9)

where p_c = reference consolidation pressure; and n = stress-state coefficient.

Fig. 2. Schematic diagram of the yield/subloading surface of the CASM-SP model based on Cui et al. (2023).

Fig. 3. Schematic diagram of conventional and PSR plastic flow in the plane of (σ_y/2 − σ_x/2, τ_xy).

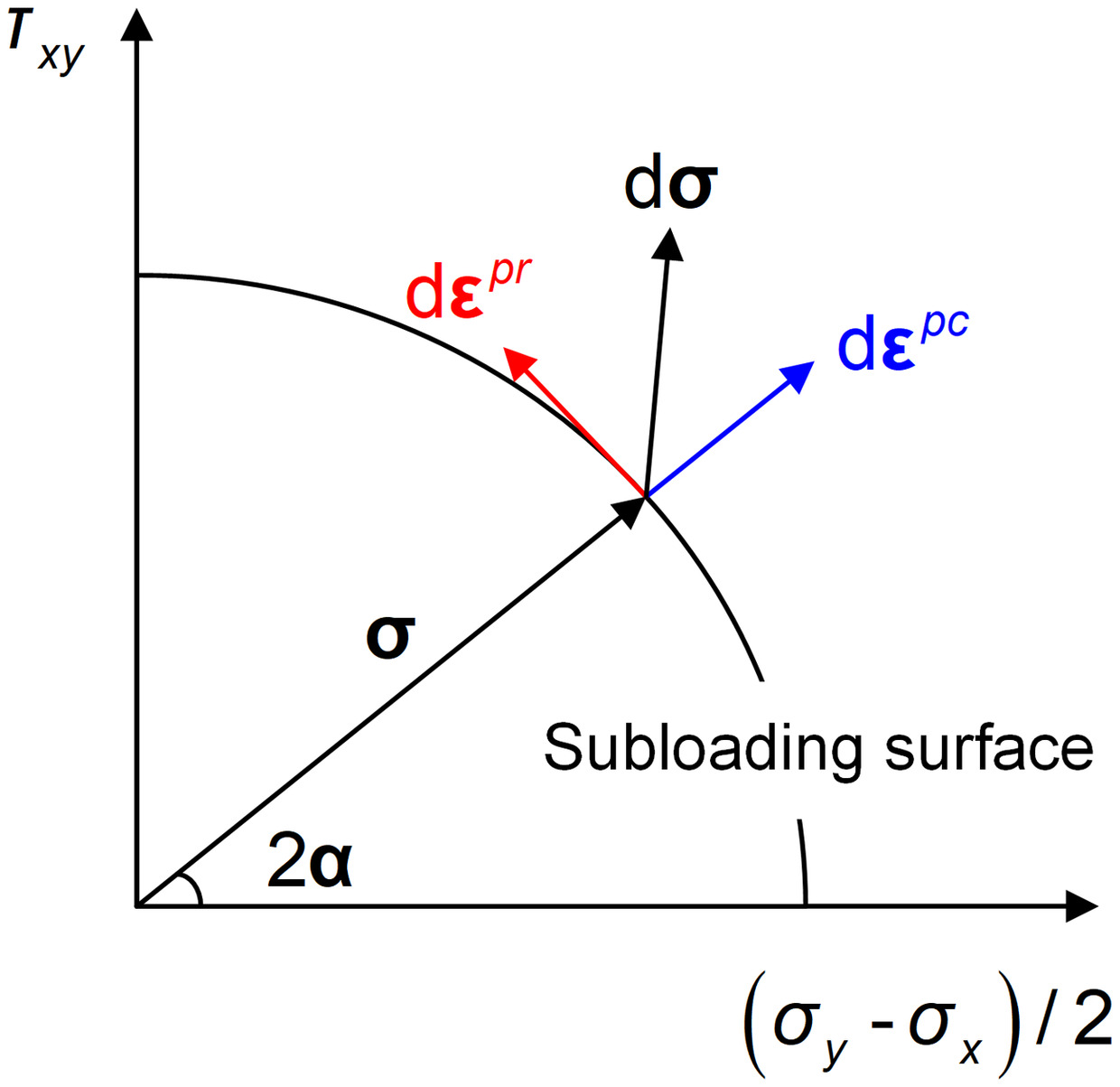
Plastic Flow Rule Considering PSR Effect

In traditional elastoplastic theory, the plastic strain increment

d ε^{p}

is typically induced by changes in the principal stress. The pure PSR loading is regarded as neutral loading within the framework of traditional elastoplastic theory and does not induce plastic deformation. This obviously contradicts the observations (Miura et al. 1986; Qian et al. 2018; Wang et al. 2019a). Therefore, to account for the influence of the direction of stress on the plastic flow, Gutierrez et al. (1991, 1993) and Lu et al. (2019) defined the following plastic flow rule:

d ε^{p} = d ε^{p c} + d ε^{p r}

(10)

where

d ε^{p c}

and

d ε^{p r}

= plastic strain increments induced by conventional and PSR loadings, respectively. For

d ε^{p c}

, it can be determined as (Lu et al. 2020)

d ε^{p c} = ⟨ d Λ^{c} ⟩ L^{c}

(11)

d Λ^{c} = \frac{1}{K_{p}^{c}} N^{c} : d σ = \frac{N^{c} : D^{e} : d ε - K D^{r} t r (N^{c}) | d Λ^{r} |}{K_{p}^{c} + N^{c} : D^{e} : L^{c}}, L^{c} = n^{c} + \frac{1}{3} D^{c} δ

(12)

where dΛ^c in the Macaulay bracket is the plastic multiplier induced by conventional loading;

L^{c}

= conventional plastic flow direction; and

K_{p}^{c}

= plastic modulus of conventional loading, and its explicit expression will be presented later. Here,

D^{e}

denotes the elastic stiffness matrix; dΛ^r and D^r denote the plastic multiplier and dilatancy rate related to PSR loading;

N^{c}

represents the partial derivative of subloading function with respect to current stress tensor;

n^{c}

denotes the unit deviatoric flow direction determined by current stress state; and D^c denotes the dilatancy rate induced by conventional loading. In this study, they can be defined as

N^{c} = \frac{\partial f}{\partial σ} = \frac{\partial f}{\partial p} \frac{\partial p}{\partial σ} + \frac{\partial f}{\partial q} \frac{\partial q}{\partial σ}

(13)

\frac{\partial f}{\partial p} = \frac{1}{p \ln r} - \frac{n q^{n}}{M^{n} p^{n + 1}}, \frac{\partial f}{\partial q} = \frac{n q^{n - 1}}{M^{n} p^{n}}, \frac{\partial p}{\partial σ} = \frac{1}{3} δ, \frac{\partial q}{\partial σ} = \sqrt{\frac{3}{2}} \frac{s}{‖ s ‖}

(14)

n^{c} = \frac{s}{‖ s ‖}, D^{c} = d^{c} [\exp (m ψ) - \frac{η}{M}]

(15)

where d^c = a model parameter used to control the evolution rate of D^c; and m = a model parameter that controls the phase transformation state of sand, and it can be selected as 0 for clay. It is worth noting that in the study of Lu et al. (2020), a Cam-clay type dilatancy function was selected to characterize the volume variation resulting from conventional loading, which could satisfactorily capture the dilatancy behavior of clay during the loading progress. To enhance the predictive capability for the shear dilation behavior of sand, this paper adopts the state-dependent dilation function defined in Eq. (15) (Been et al. 1991; Xiao et al. 2017, 2018 2019, 2020).

Furthermore, inspired by the work of Wang et al. (2016) and Lu et al. (2020), the plastic strain associated with the PSR loading mechanism can be defined as follows:

d ε^{p r} = d Λ^{r} N^{r} + \frac{1}{3} | d Λ^{r} | D^{r} δ

(16)

where dΛ^r = plastic multiplier induced by PSR loading;

N^{r}

= deviatoric plastic flow direction of PSR loading; and D^r = dilatancy rate related to the PSR loading mechanism. According to the work of Wang et al. (2016, 2022) and Lu et al. (2019, 2020), dΛ^r and

N^{r}

can be given as (plane strain condition)

d Λ^{r} = \frac{2 G w}{K_{p}^{r} + 2 G w} N^{r} : d ε, w = ⟨ 1 - {(η / M)}^{m} ⟩, K_{p}^{r} = h^{r} {(\frac{M^{2} - η^{2}}{2 η})}^{0.2}

(17)

N^{r} = {- a, a, 0, b}^{T}

(18)

\begin{aligned} a & = \frac{N_{x y}^{c}}{\sqrt{{(N_{x x}^{c} - N_{y y}^{c})}^{2} / 4 + {(N_{x y}^{c})}^{2}}}, \\ b & = \frac{(N_{x x}^{c} - N_{y y}^{c}) / 2}{\sqrt{{(N_{x x}^{c} - N_{y y}^{c})}^{2} / 4 + {(N_{x y}^{c})}^{2}}} \end{aligned}

(19)

where the function w in the Macaulay bracket is used to ensure that the plastic flow associated with the PSR is frozen when η > M. The parameter m (selected as 50 in this paper) is a large positive number, ensuring that w approaches 1 when η < M (Lu et al. 2020). Here,

K_{p}^{r}

denotes the plastic modulus of PSR loading; and h^r is a model parameter that controls the evolution of

K_{p}^{r}

.

Given that the flow deformation of soil under pure PSR loading depends on its state, this study incorporates a state-dependent dilatancy rule to characterize the volumetric deformation behavior under PSR loading:

D^{r} = d^{r} [\exp (m ψ) - \frac{η}{M}] [1 - \exp (- 100 ε_{c u m}^{p r})]

(20)

ε_{cum}^{p r} = \int_{0}^{t} ‖ d ε^{p r} ‖ d t

(21)

where d^r = a material parameter controlling the rate of dilatancy associated with PSR loading; and

ε_{cum}^{p r}

= cumulative plastic strain induced by PSR loading. It should be noted that the right term in Eq. (20) was introduced by Yang and Yu (2010) and Lu et al. (2020), and the purpose of introducing this term is to avoid numerical issues that may arise during the initial loading stages.

Hardening Law

Within the framework of the PSR plastic flow rule defined in the previous section, it is commonly assumed that the hardening (softening) behavior is induced by the conventional plastic strain rate

d ε^{p c}

(Lu et al. 2020; Wang et al. 2022). The CASM-SP model introduces two hardening variables, p_c and R. Based on the well-known Cam-clay plasticity, the evolution rule of p_c can be given as

d p_{c} = \frac{(1 + e_{0}) p_{c}}{λ - κ} d ε_{v}^{p c}

(22)

d ε_{v}^{p c} = \sqrt{\frac{2}{3}} D^{c} d Λ^{c}

(23)

where

d ε_{v}^{p c}

= plastic volumetric strain increment; and e₀ = initial void ratio. Furthermore, based on the assumption of the subloading surface theory (Hashiguchi 1989, 2009), the subloading surface gradually approaches the yield surface with the progress of plastic loading. Consequently, the evolution of R can be defined as follows:

d R = U ‖ d ε^{p c} ‖ = U d Λ^{c} ‖ L^{c} ‖

(24)

where U = a monotonically decreasing function related to R, designed to ensure that the subloading surface never exceeds the yield surface. It should be noted that

‖ d ε^{p c} ‖ \neq d Λ^{c}

for soil because

L^{c}

contains the information from both the volumetric and deviatoric directions. According to the work of Hashiguchi (1989) and (Hashiguchi et al. 1996), U can be simply defined as

U = - u \ln (R)

(25)

where u = a material parameter controlling the evolution rate of the subloading surface. It should be noted that before using CASM-SP for simulations, it is necessary to determine the initial values of both R and p_c. The determination method can be referred to the work of Cui et al. (2023, 2024).

Furthermore, based on the consistency condition of the subloading surface (Cui et al. 2023, 2024), the coaxial loading plastic modulus

K_{p}^{c}

of CASM-SP can be defined as follows:

K_{p}^{c} = - \frac{\partial f}{\partial R} \frac{\partial R}{\partial ‖ ε^{p c} ‖} ‖ L^{c} ‖ - \frac{\partial f}{\partial p_{c}} \frac{\partial p_{c}}{\partial ε_{v}^{p c}} \sqrt{\frac{2}{3}} D^{c}

(26)

where the explicit form of the partial derivatives in Eq. (26) can be expressed as

\frac{\partial f}{\partial R} = - \frac{1}{R \ln r}, \frac{\partial R}{\partial ‖ ε^{p c} ‖} = U

(27)

\frac{\partial f}{\partial p_{c}} = - \frac{1}{p_{c} \ln r}, \frac{\partial p_{c}}{\partial ε_{v}^{p c}} = \frac{(1 + e_{0}) p_{c}}{λ - κ}

(28)

General Stress‒Strain Relation

According to the elastic theory, the relationship between the stress rate and strain rate can be given as

d σ = D^{e} : d ε^{e}, d ε^{e} = d ε - d ε^{p} = d ε - d ε^{p c} - d ε^{p r}

(29)

where

d ε^{e}

= elastic strain increment; and

D^{e}

= elastic stiffness tensor, which can be given as

D^{e} = (K - \frac{2}{3} G) δ \otimes δ + 2 G I

(30)

K = \frac{1 + e_{0}}{κ} p

(31)

G = \frac{3 (1 - 2 μ)}{2 (1 + μ)} K

(32)

where K and G = elastic bulk and shear modulus, respectively; and μ = Poisson's ratio.

By substituting Eqs. (11) and (16) into Eq. (29), the general stress–strain relationship of CASM-SP can be given as

d σ = D^{e} : (d ε - d ε^{p c} - d ε^{p r})

(33)

Model Parameters

The newly proposed model introduces the following model parameters:

e_{Γ}

, M, λ, κ, μ, r, n, u, h^r, d^c, d^r, and m. Among these, parameters

e_{Γ}

, M, and λ establish the critical state of soil and are referred to as critical state parameters, while parameters κ and μ define the elastic response of soil and are denoted as elastic parameters. It should be noted that

e_{Γ}

, M, λ, κ_, and μ are shared with the Cam-clay type models, and their calibration methods can be referenced from earlier investigations (Budhu 2010; Roscoe 1963).

The parameters r and n are termed yield parameters in this study due to their influence on shaping the yield surface, and their typical calibration procedure can be found in the study of Rios et al. (2016). Alternatively, in cases where establishing precise values for r and n proves challenging, the recommended typical values presented by Yu (2007) can be applied.

The parameters u and h^r are identified as hardening parameters in this study. Parameter u, initially introduced by Hashiguchi (1989), governs the evolution rate of the subloading surface. According to a study of Hashiguchi (2017), u can be calibrated through the stress‒strain relationship of conventional triaxial tests. However, parameter h^r, pioneered by Lu et al. (2020), defines the plastic modulus of the PSR mechanism. It can be determined by fitting the stress‒strain response of the pure PSR test.

The parameters d^c, d^r, and m are categorized as dilatancy parameters. Among these parameters, d^c and m were introduced by Li and Dafalias (2000) to account for the state-dependent dilatancy behavior of sand. Specifically, the parameter d^c dictates the evolution rate of the dilatancy behavior during conventional loading, and it can be determined by fitting volume changes observed in triaxial drainage experiments. The parameter m defines the phase transformation of a granular material, and it is determined by fitting the effective stress path from a triaxial undrained experiment. The parameter d^r determines the dilatancy rate under PSR loading and can be calibrated by fitting the stress‒dilatancy response of the pure PSR test.

Model Validation

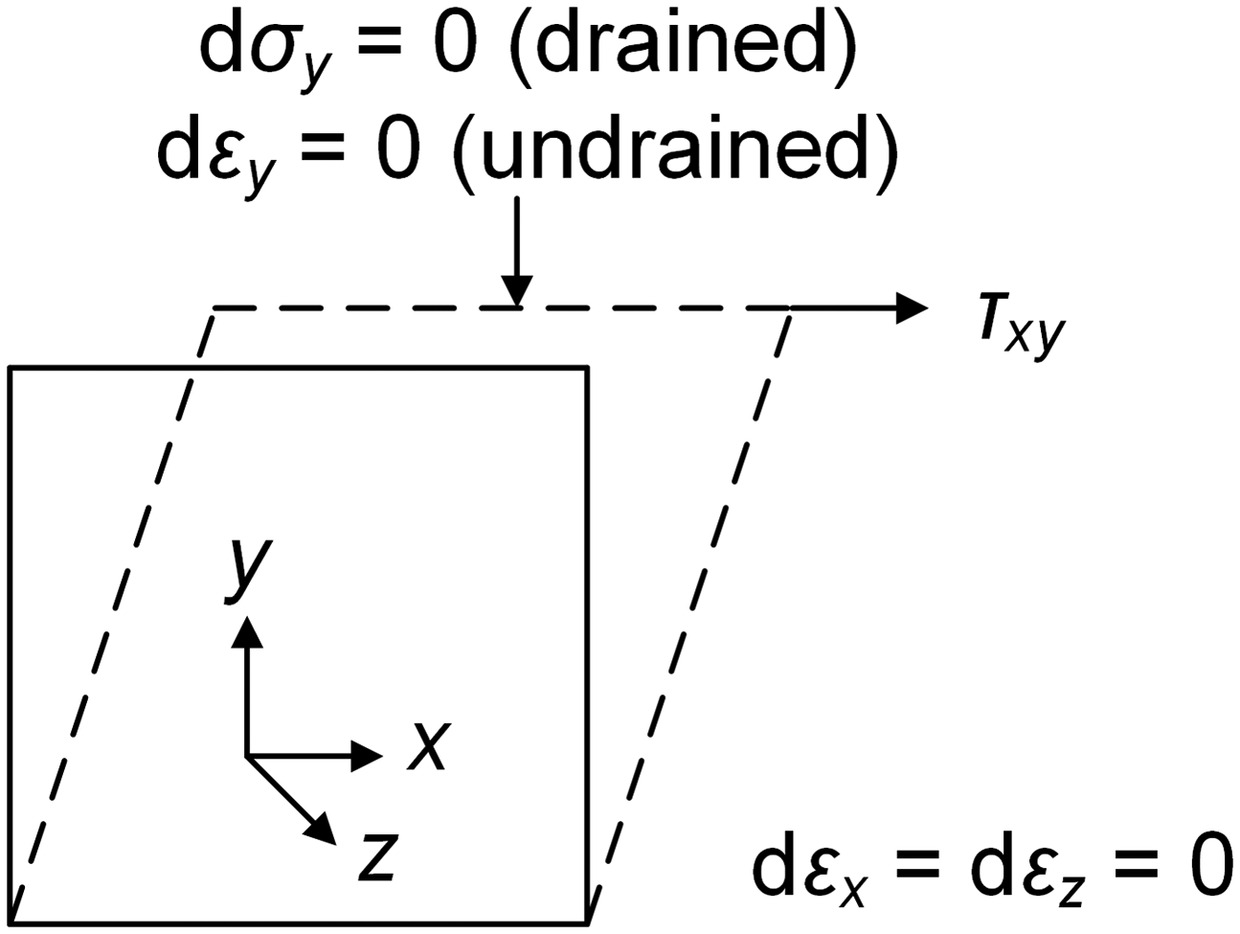
To validate the reliability and applicability of the CASM-SP model, a series of experimental and FEM test data under drained and undrained simple shear tests are employed in this study. The schematic representation of the boundary conditions of simple shear deformation can be found in Fig. 4, and the material parameters used for the simulations are listed in Table 1. Additionally, the principal stress direction α, principal strain increment direction β, and principal stress direction ξ are defined as follows:

\begin{aligned} α & = \frac{1}{2} \tan^{- 1} (\frac{2 τ_{x y}}{σ_{y} - σ_{x}}), β = \frac{1}{2} \tan^{- 1} (\frac{d γ_{x y}}{d ε_{y} - d ε_{x}}), \\ ξ & = \frac{1}{2} \tan^{- 1} (\frac{2 d τ_{x y}}{d σ_{y} - d σ_{x}}) \end{aligned}

(34)

where σ_x, σ_y, and τ_xy represent the horizontal, vertical, and shear stress, respectively. Furthermore,

ε_{x}

,

ε_{y}

, and γ_xy represent the horizontal, vertical and shear strain, respectively. In addition, the noncoaxial angle θ = β − α.

Fig. 4. Boundary conditions of drained and undrained simple shear test.

Table 1. Material parameters of CASM-SP

Parameters	Weald clay	Bangkok clay	Fontainebleau sand	Hutcheson sand
Critical state parameters	$e_{Γ}$ = 1.06	$e_{Γ}$ = 1.751	$e_{Γ}$ = 1.11	$e_{Γ}$ = 1
	M = 0.9	M = 0.71	M = 1.01	M = 1.28
	λ = 0.093	λ = 0.191	λ = 0.055	λ = 0.075
Elastic parameters	κ = 0.025	κ = 0.028	κ = 0.004	κ = 0.005
Elastic parameters	μ = 0.3	μ = 0.41	μ = 0.35	μ = 0.2
Yield parameters	r = 2.714	r = 2.718	r = 20	r = 75
Yield parameters	n = 4.5	n = 1	n = 1	n = 1.5
Hardening parameters	u = 0.1	u = 45	u = 0.8	u = 4
Hardening parameters	h^r = 65 (MPa)	h^r = 150 (MPa)	h^r = 950 (MPa)	h^r = 800 (MPa)
Dilatancy parameters	d^c = 1	d^c = 0.1	d^c = 0.9	d^c = 1.5
	d^r = 0.5	d^r = 0.2	d^r = 0.01	d^r = 1
	m = 0	m = 0	m = 0.2	m = 0.5

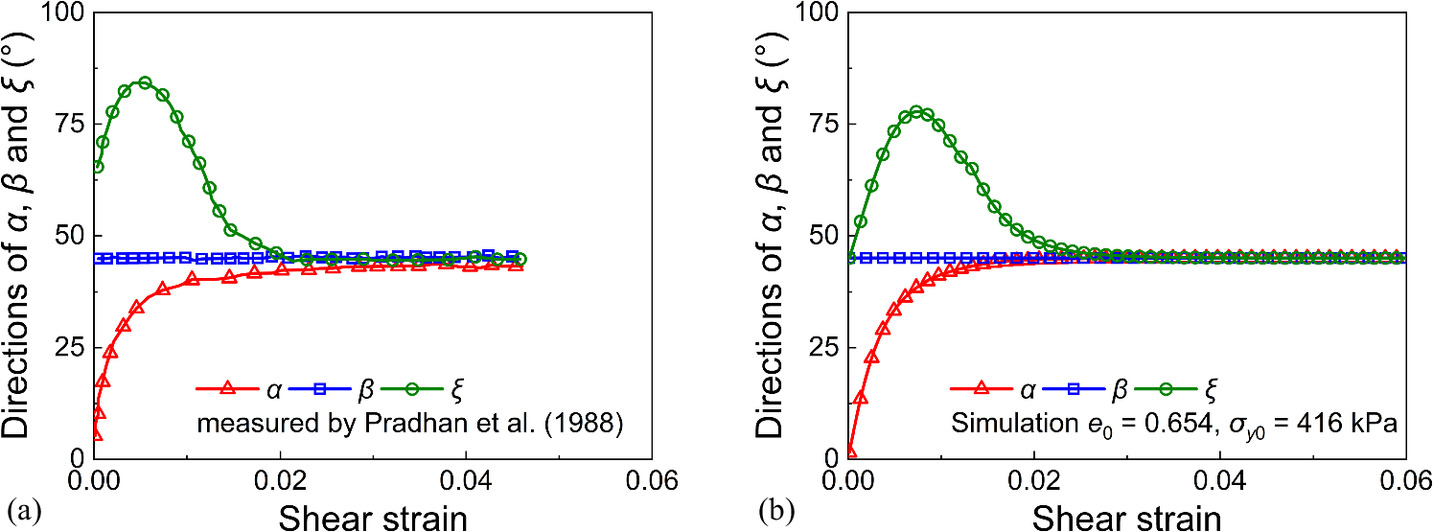
To validate the capability of the CASM-SP model to predict the noncoaxial behavior of soil, the FEM test data from Yang and Yu (2006a) are used in this study. Distinguishing from the CASM-SP model, they extended the CASM model to the noncoaxial state through the application of the yield vertex theory. In their tests, they used the material parameters of Weald clay (Yu 1998) to examine the ability of the proposed model to predict the noncoaxial behavior of soil. The specimens were first normally consolidated with K₀ = 0.5 and 1.81 and then subjected to a drained simple shear test. It should be noted that in their work,β was defined by the plastic strain increment, that is,

β = (1 / 2) \tan^{- 1} (((d γ_{x y}^{p}) / (d ε_{y}^{p} - d ε_{x}^{p})))

. Figs. 5–7 compare the measured and predicted data of the evolutions of α, β, and θ of normally consolidated Weald clay. It can be found that there is an obvious deviation between α and β during the initial loading stage. However, the difference between α and β decreases with the shearing continues. At the final stage, coaxiality is achieved. Fig. 8 illustrates the evolutions of α and β of overconsolidated Weald clay (OCR = 24) predicted by Yang and Yu (2006a) and CASM-SP. It should be noted that for overconsolidated soil, the initial stress state lies within the yield surface. The model of Yang and Yu (2006a) obeys the conventional elastoplastic theory and predicts pure elastic deformation before the stress state exceeds the yield surface. Therefore, the evolution of β calculated by Yang and Yu (2006a) is slower than that by CASM-SP at the initial loading stage. Despite these differences, the calculation results of Yang and Yu (2006a) and CASM-SP tend to converge as loading continues. These comparisons demonstrate that CASM-SP can effectively simulate the noncoaxial behavior of anisotropically consolidated soil under simple shear loading.

Fig. 5. Evolutions of α and β of normally consolidated Weald clay under drained simple shear test with K₀ = 0.5: (a) data measured by Yang and Yu (2006a); and (b) simulation of CASM-SP.

Fig. 6. Evolutions of α and β of normally consolidated Weald clay under drained simple shear test with K₀ = 1.81: (a) data measured by Yang and Yu (2006a); and (b) simulation of CASM-SP.

Fig. 7. Evolution of θ of normally consolidated Weald clay under drained simple shear test with different K₀: (a) data measured by Yang and Yu (2006a); and (b) simulation of CASM-SP.

Fig. 8. Evolutions of α and β of overconsolidated Weald clay (OCR = 24) under drained simple shear test with K₀ = 2.81: (a) data measured by Yang and Yu (2006a); and (b) simulation of CASM-SP.

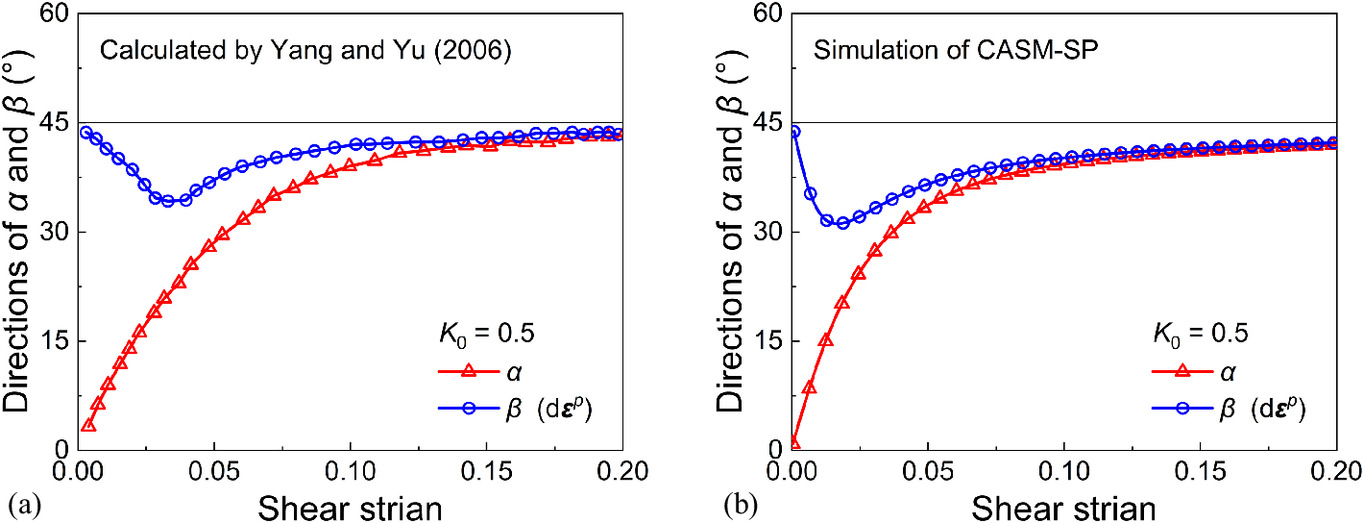
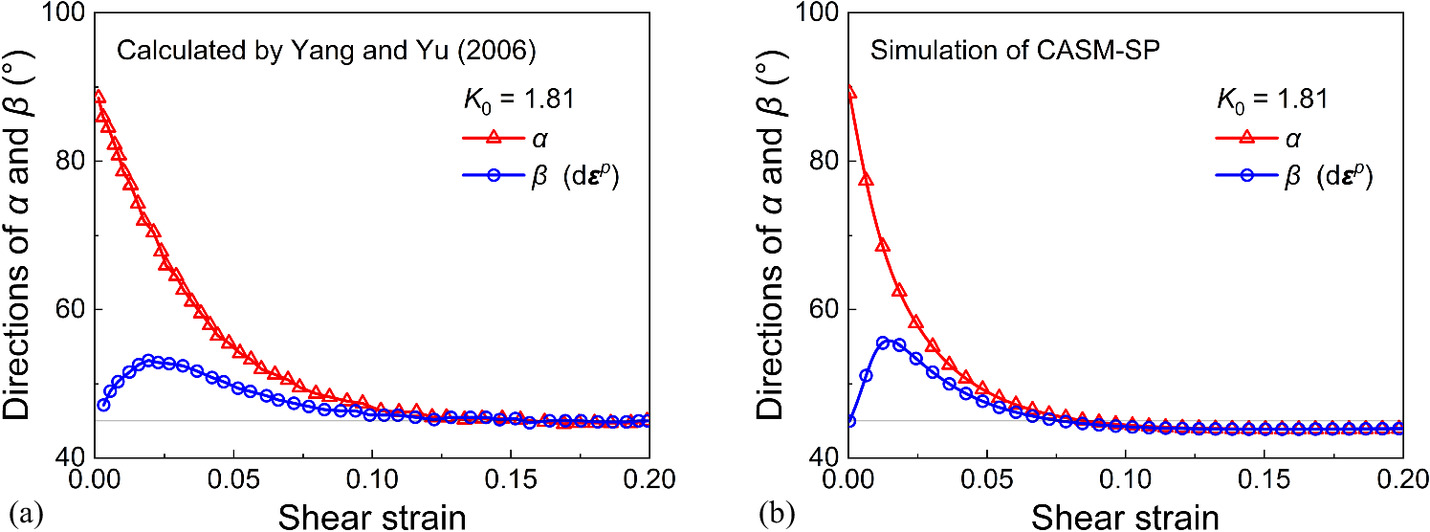
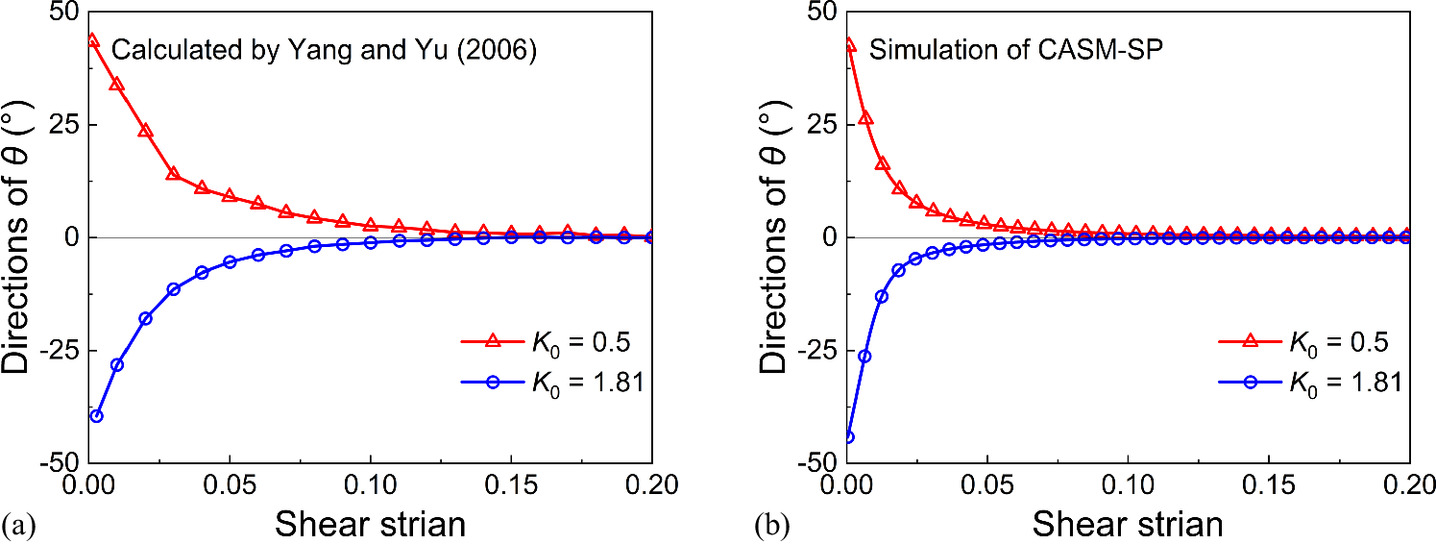
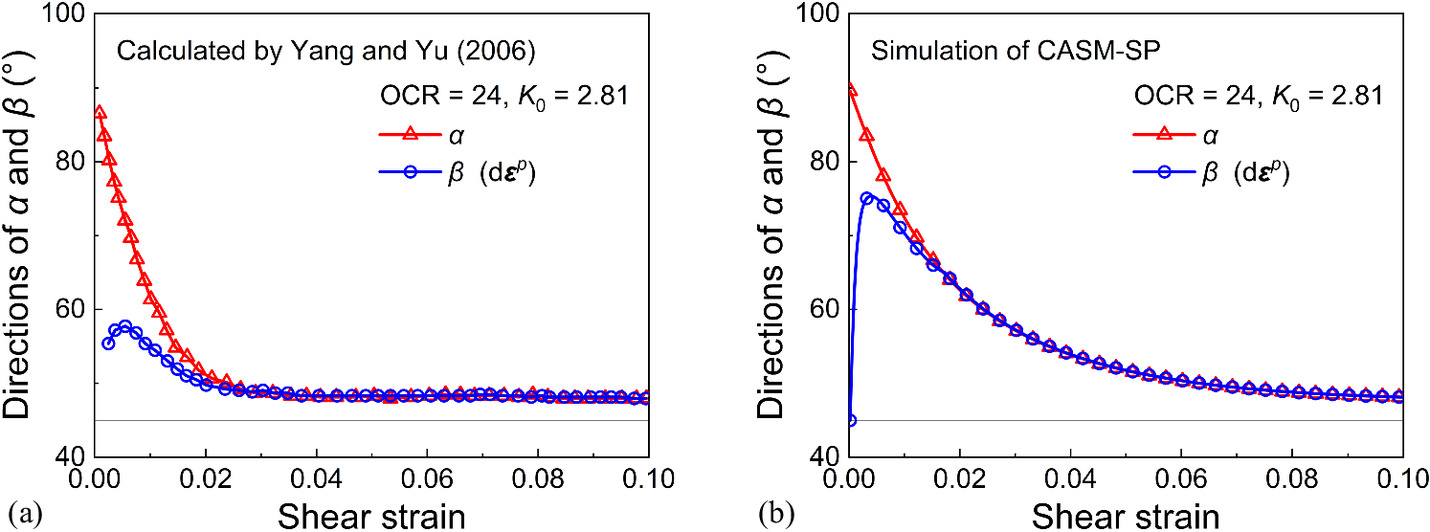
Fig. 9 presents a comparison between the experimental and simulation outcomes for normally consolidated Bangkok clay under undrained simple shear loading conditions. The experimental data were reported by Apriadi et al. (2008). In their experiment, Bangkok clay was first consolidated at vertical stresses of 200, 300, 400, and 500 kPa for K₀ = 0.68. Subsequently, the specimens underwent simple shear loading until reaching a shear strain of 0.2. Notably, the model parameters used in the simulations were taken from the experimental report in which the compression index λ and swelling index κ were obtained by converting the plasticity index I_p (Nakase et al. 1988). Figs. 9(a and b) demonstrate that the CASM-SP satisfactorily reproduces the stress–strain relations and effective paths of Bangkok clay under various vertical stress conditions.

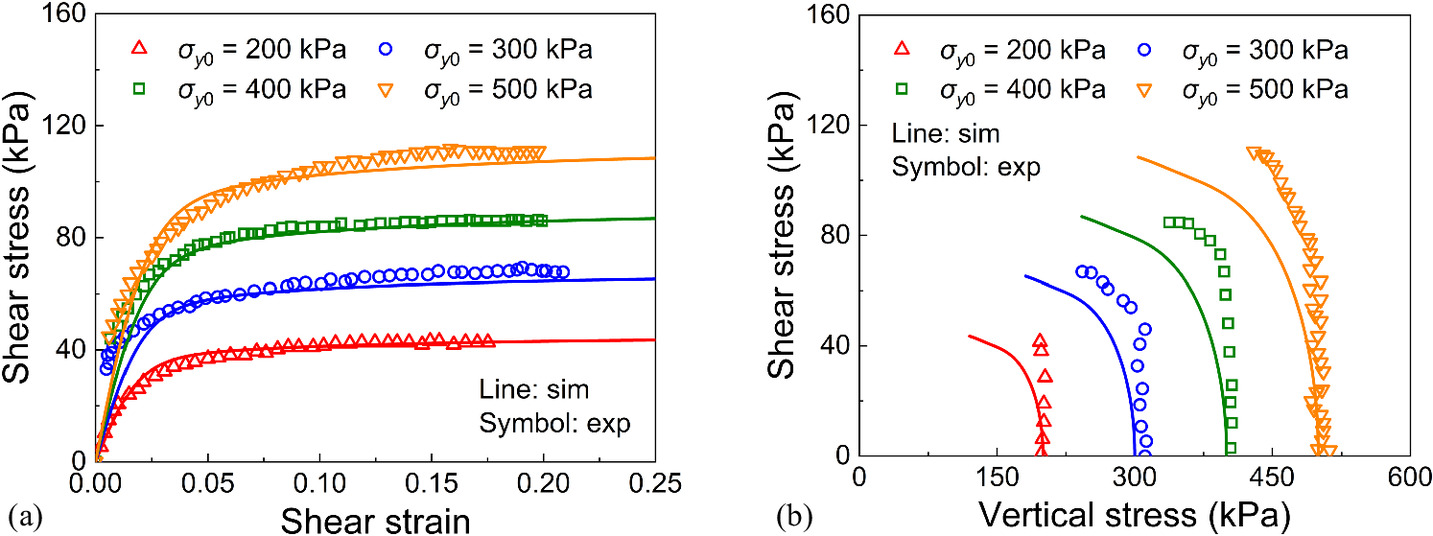
Fig. 9. Experimental data and simulation results of normally consolidated Bangkok clay under undrained simple shear test: (a) stress–strain relation; and (b) effective stress paths.
(Data from Apriadi et al. 2008.)

Fig. 10 compares the experimental and predicted results of dense Fontainebleau sand under drained simple shear tests. The experimental data can be found in the work of Andria-Ntoanina et al. (2010) and Wu et al. (2021). In the tests, the samples were prepared with different initial void ratios: e₀ = 0.678 and 0.688, and different initial vertical stress of 208 and 416 kPa. Due to the absence of the value of K₀ in the tests, the value of K₀ used for simulation was estimated using an empirical formula K₀ = 1 − sin φ, where φ denotes the internal friction angle. Then, these samples were simple sheared under drained conditions until the shear strain reaches 0.2. As depicted in Fig. 10, the CASM-SP effectively predicts both the stress‒strain relationship and dilatancy behavior of Fontainebleau sand under the simple shear test. Furthermore, to verify the ability of CASM-SP to describe the noncoaxial behavior of the sand under undrained simple shear tests, the model predictions are compared with the experimental patterns of dense Toyoura sand measured by Pradhan et al. (1988). As in Fig. 11, both Toyoura sand and Fontainebleau sand exhibit similar flow characteristics under undrained simple shear conditions: the principal strain direction β maintains a steady angle of 45°, and the principal stress direction α gradually advances toward 45°. Additionally, the direction of the principal stress increment ξ experiences rapid increase during the initial loading stage, decreases with continued loading, and eventually stabilizes around 45°.

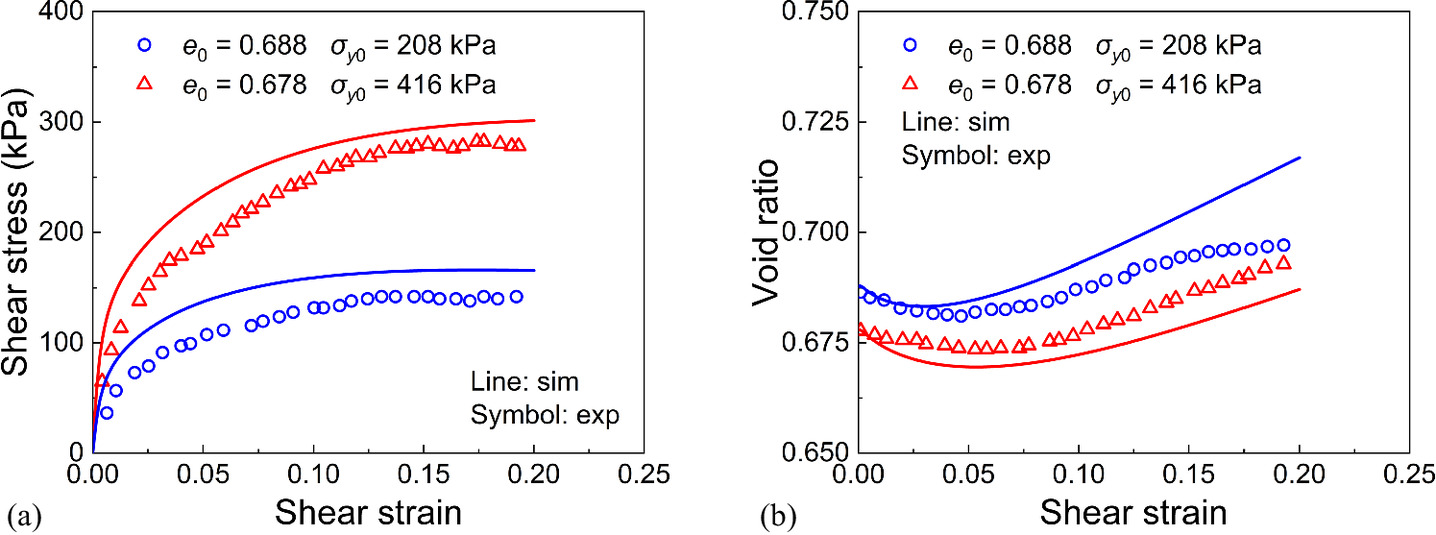
Fig. 10. Experimental data and simulation results of dense Fontainebleau sand under drained simple shear test: (a) stress–shear relation; and (b) void ratio–strain relation.
(Data from Andria-Ntoanina et al. 2010; Wu et al. 2021.)

Fig. 11. Noncoaxial behavior of dense sand under undrained simple shear test: (a) data measured by Pradhan et al. (1988); and (b) simulation results of Fontainebleau sand.

To examine the complete stress state of soil under simple shear conditions, Ghafghazi et al. (2023) conducted a series of drained and undrained simple shear tests on Hutcheson sand using an advanced simple shear apparatus. The relative densities of these specimens varied from D_r = 35% to 88%, with the maximum and minimum void ratios of 0.877 and 0.602, respectively. The specimens were first consolidated under K₀ conditions, and then sheared under both drained and undrained conditions. It should be noted that in the tests of Ghafghazi et al. (2023), the z-direction is taken as the vertical direction, whereas in this study, the y-direction is considered as the vertical direction. Fig. 12 compares the experimental and simulated results of the evolution of stress components of Hutcheson sand with different D_r under undrained conditions. Overall, the CASM-SP reasonably predicted the variation in the stress components. Fig. 13 depicts the experimental and simulation pore pressures of Hutcheson sand under undrained conditions, where the pore pressures are defined as follows:

Δ u_{y} = σ_{y 0} - σ_{y}, Δ u_{x} = σ_{x 0} - σ_{x}, Δ u = p_{0} - p

(35)

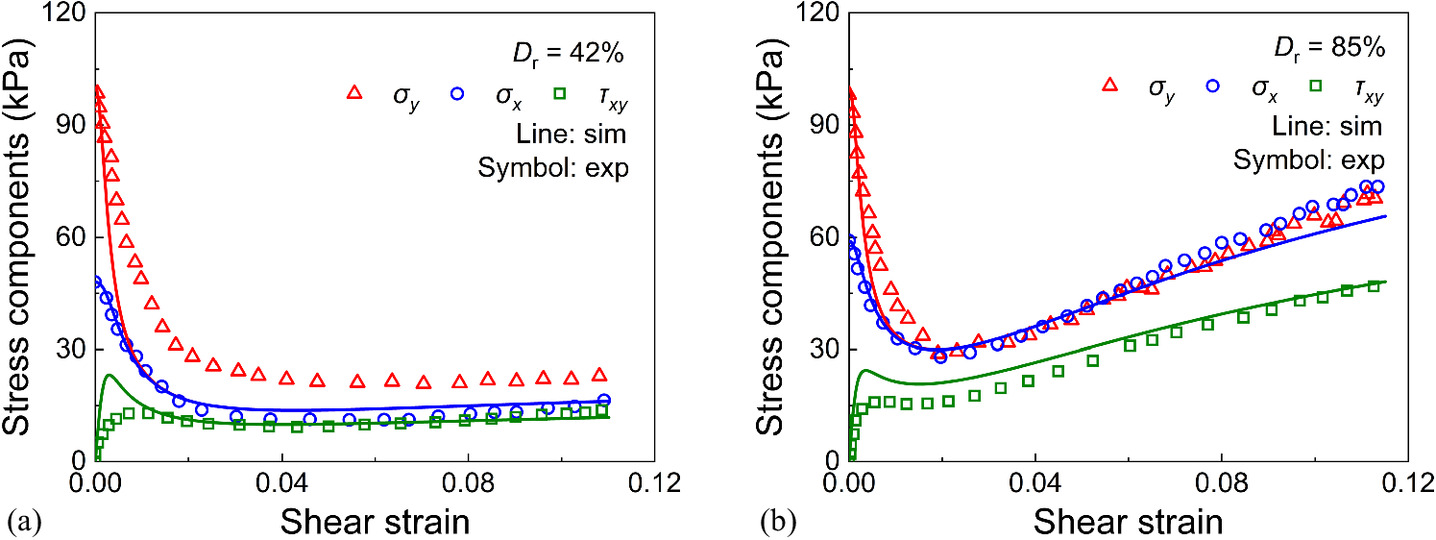
Fig. 12. Evolutions of stress components of Hutcheson sand under undrained simple shear test with different relative densities: (a) D_r = 42%; and (b) *D_r* = 85%.
(Data from Ghafghazi et al. 2023.)

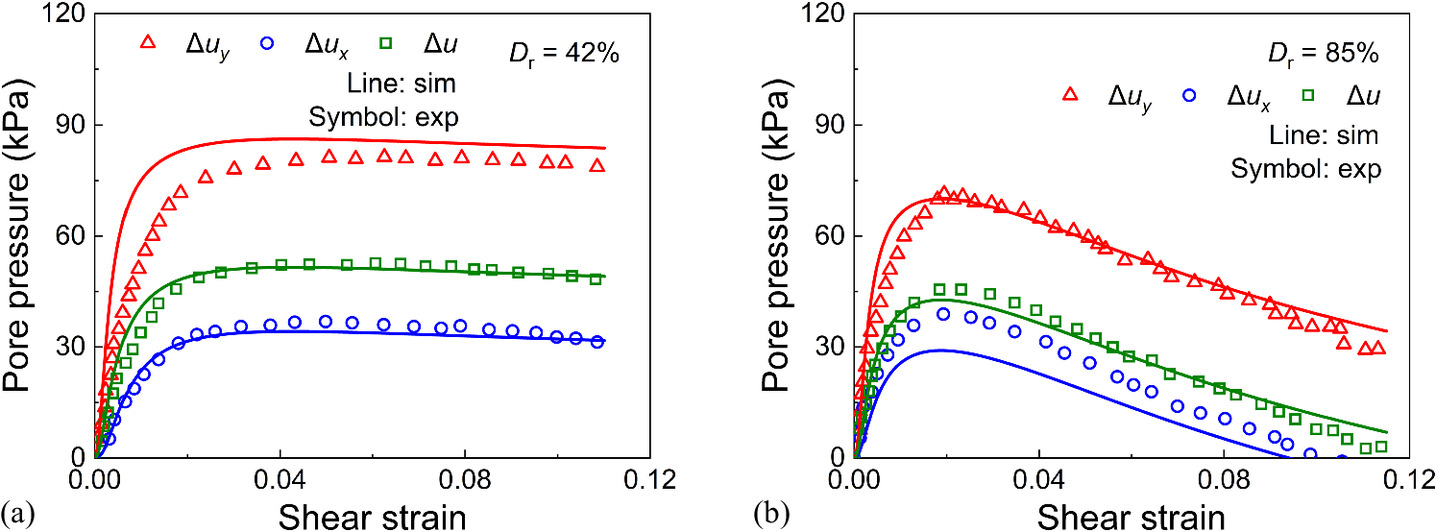
Fig. 13. Evolutions of pore pressures of Hutcheson sand under undrained simple shear test with different relative densities: (a) *D_r* = 42%; and (b) *D_r* = 85%.
(Data from Ghafghazi et al. 2023.)

From Fig. 13, the predicted results are consistent with the experimental data in terms of trends. Figs. 14 and 15 compare the Mohr circles of Hutcheson sand with different D_r under both drained and undrained conditions. It can be found in Figs. 14(a) and (15a) that the drained tests generate the larger Mohr circle, while the undrained tests generate the smaller circle. For loose samples (D_r = 35% and 42%), a unique envelope of the mobilized friction angle (φ_mob = 40°) can be drawn tangent to the two circles plotted by drained and undrained tests. While for dense samples (D_r = 85% and 88%), the mobilized friction angle φ_mob = 42°. Figs. 14(b) and (15b) depict the simulation results of CASM-SP, where the Mohr circles are determined by passing through the final point of the effective path (σ_y and τ_xy) and being tangent to two mobilized friction angle envelopes. It can be found that the predicted Mohr circles and effective stress paths closely match the experimental observations.

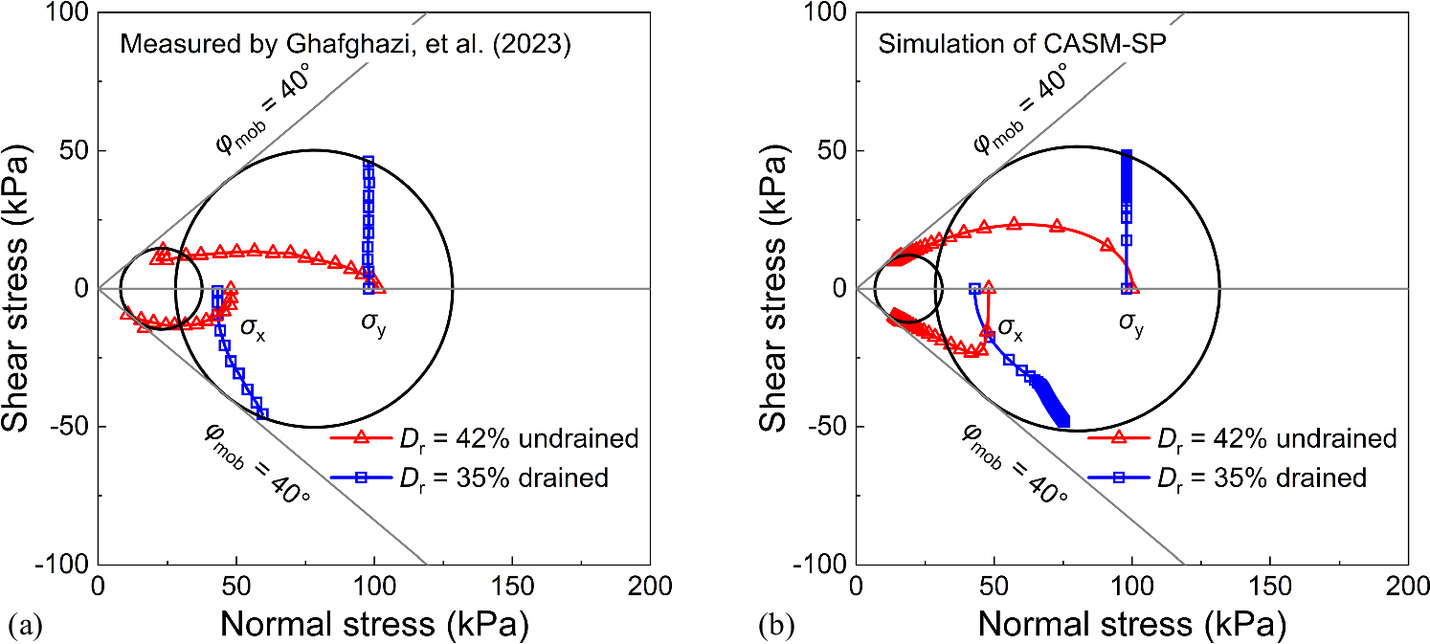
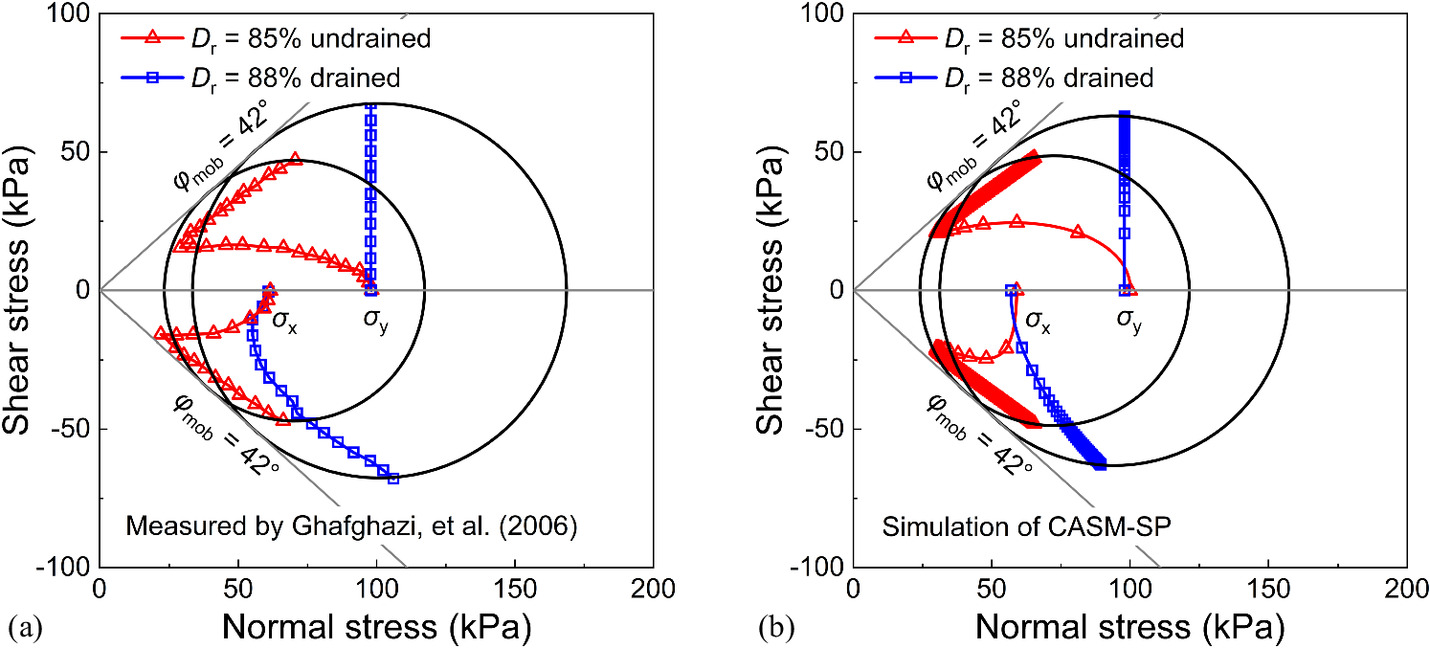
Fig. 14. Mohr circles of loose Hutcheson sand under drained and undrained simple shear tests: (a) data measured by Ghafghazi et al. (2023); and (b) simulation results of CASM-SP.

Fig. 15. Mohr circles of dense Hutcheson sand under drained and undrained simple shear tests: (a) data measured by Ghafghazi et al. (2023); and (b) simulation results of CASM-SP.

Conclusions

This study developed a novel unified critical state constitutive model, denoted as CASM-SP, to predict mechanical responses of both clay and sand during the simple shear loading, where effects of the direction of stress increment has been incorporated into the establishment of the plastic flow rule. The newly developed CASM-SP model was demonstrated to effectively describe the mechanical response of soil induced by PSR mechanism under simple shear conditions through a series of experimental data. Conclusions can be drawn as follows.

1.

The simulation results of normally and overconsolidated clay under both drained and undrained simple shear conditions were in good agreement with the FEM and experimental data.

2.

The CASM-SP model can reasonably predict the simple shear response of sand with different relative density under drained and undrained conditions, such as the shear dilation, strain hardening (softening), noncoaxial behavior, strength envelopes, and so forth.

3.

This simple model can be a benchmark and allow for further development to account for more complex loading conditions involving principal stress rotations. For instance, such developments could involve the incorporation of variables such as the Lode angle or the fabric tensor.

Data Availability Statement

Some or all data, models, or code that support the findings of this study are available from the corresponding author upon reasonable request.

Acknowledgments

This study was supported by the National Natural Science Foundation of China (Grant Nos. 52278413, 51609204, 42011530170, 42077236), by Sichuan Science and Technology Program (Grant No. 2022NSFSC0407), and by China Postdoctoral Science Foundation (Grant No. 2021M702718).

References

Andria-Ntoanina, I., J. Canou, and J. Dupla. 2010. Caractérisation mécanique du sable de Fontainebleau NE34 à l’appareil triaxial sous cisaillement monotone. Marne-La Vallée: Laboratoire Navier-Géotechnique (CERMES, ENPC/LCPC).

Abstract

Introduction

Constitutive Relation of CASM-SP: Development and Implementation

Critical State Theory, a Brief Review

Yield Criterion and Subloading Function of CASM-SP

Plastic Flow Rule Considering PSR Effect

Hardening Law

General Stress‒Strain Relation

Model Parameters

Model Validation

Conclusions

Data Availability Statement

Acknowledgments

References

Information

Published In

Copyright

History

ASCE Technical Topics:

Authors

Affiliations

Metrics

Citations

Download citation

Figures

Other

Share

Copy the content Link

Share with email

Share

Request Username

Create a new account

Change Password

Password Changed Successfully

Verify Phone

Congrats!