Structural System Reliability: Overview of Theories and Applications to Optimization
Publication: ASCE-ASME Journal of Risk and Uncertainty in Engineering Systems, Part A: Civil Engineering
Volume 7, Issue 2
Abstract
This paper provides an overview of theories and applications of structural system reliability (SSR). The paper defines SSR problems and discusses the growing needs for SSR analysis and technical challenges. Detailed literature reviews are provided for three subtopics: SSR methods for Boolean system events, SSR methods for sequential failures, and SSR-based design/topology optimization. Discussions of each subtopic define the target problem using mathematical formulations and categorize existing SSR methods in terms of the characteristics of the problems and approaches. The paper summarizes SSR methods that are considered critical in the history and have introduced notable technological developments in recent years. In each subtopic or category, the reviewed methods are compared with each other in terms of accuracy, computational efficiency, and implementation issues to allow identifying apposite methods for SSR applications. The paper concludes with remarks on future research needs and opportunities.
Introduction
In assessment of the reliability of a structure with regard to safety and/or functionality, its limit state is often defined in terms of multiple components which represent
•
structural members, such as beams, columns, plates, and cables;
•
failure-prone locations or subsystems, such as hot spots, building floors, and bridge decks;
•
failure mechanisms, such as sway, beams, and combined mechanisms of ductile frames;
•
generalized forces, such as bending moment, shear, and torsion;
•
discretized time points in the time history of a structural response; and
•
combinations of the aforementioned components.
So-called component reliability analysis (Der Kiureghian 2005; Melchers and Beck 2018) deals with the limit state of a single component at a time. There are many well-established component reliability analysis methods in the literature.
On the other hand, structural system reliability (SSR) is defined as the probability that the structural system remains functional and/or safe despite the occurrence of component failures (Der Kiureghian 2006; Byun and Song 2017). Currently, the importance of SSR analysis is ever-growing in structural engineering practice because (1) structures are becoming more complex in terms of topology, typology, behavior, interdependency between components or subsystems, and so forth; (2) the size of structural systems is increasing; (3) there are pressing needs to implement a proper level of structural redundancy through system reliability analysis; and (4) performance-based design and optimization require a holistic system-level evaluation of the structural reliability.
In general, methods originally developed to assess component reliability can be intrinsically limited for SSR assessment, which requires handling multiple components. Moreover, SSR analysis involves unique technical challenges, which are mainly caused by (1) statistical dependence between component events caused by common source effects, capacity correlations, and so forth; (2) causal effects such as load redistribution after local failures; (3) complexity of SSR problems in terms of size and system failure definition; (4) additional computational costs; (5) integration with decision-making schemes or optimization; and (6) lack of complete information on the marginal and joint failure probabilities of components. In recent decades, rapid technological developments have facilitated SSR analysis for a wide class of applications. However, many researchers and practitioners apparently find it difficult to understand unique challenges in SSR assessment and identify the best choice of the SSR method for a given problem setting. Therefore, this paper provides an overview of SSR methods to promote applications of SSR methods and identify future research needs and opportunities.
Based on the research experiences of the authors in this field, this paper provides an overview of (1) SSR methods for Boolean system events; (2) SSR methods for sequential failures; and (3) applications of SSR to design/topology optimization. The first part serves as an introduction to the definition of general SSR problems and summarizes recent technical developments in time-invariant and time-variant SSR analysis described by Boolean expressions. The second part first defines sequential failure problems in structural reliability context and explains the technical challenges, and then introduces various approaches—numerical, response-surface-based, and failure path approaches—with a focus on recent developments. The third part discusses how SSR is being integrated with the decision-making process such as reliability-based design and topology optimization. Six different approaches are introduced, with a focus on how SSR is implemented in the optimization procedures. Because of the length limit, this review paper focuses on system reliability analysis methods developed for structural systems. However, there is vast literature on general system reliability methods (Verma et al. 2010; Mettas and Savva 2001) and nonprobabilistic or hybrid methods (Adduri and Penmetsa 2009; Cheng et al. 2019; Kang and Luo 2009) that could be applied to structural systems.
This review paper first defines the general problem setting, and then provides a critical review of important SSR methods in the literature, which are categorized in terms of their approach to the given type of problem. Common criteria are used for the evaluation and comparison of the methods reviewed in each part to allow identifying the best candidates for given SSR problems. The review generally focuses on recently developed technologies but includes classic methods as well to explain the history of the technological developments in SSR. This approach naturally focused the review in this paper on methods originally developed for SSR, but other general-purpose reliability methods developed could perform well in SSR analysis and its applications to optimization. The paper concludes with a summary and a list of important remaining challenges and opportunities which the research community needs to address.
SSR Methods for Boolean System Events
A critical civil infrastructure is a system the performance of which can be described as a logical (Boolean) function of components with binary or multiple states based on associated performance criteria (Der Kiureghian 2006). Significant efforts have been made to tackle the difficulties in the estimation of the reliability of complex structural systems caused by a large number of components or failure modes and a high parametric dimensionality while considering the statistical dependence between components. This section comprehensively reviews SSR methods for Boolean system events by expanding upon reviews in the literature (Melchers and Beck 2018; Der Kiureghian 2006; Byun and Song 2017; Thoft-Christensen and Murotsu 2012).
Mathematical Formulation of System Reliability Problem
This section provides the mathematical formulations of system events using Boolean functions. A system is an assembly of components that can have multiple states and can be described as a series, parallel, or general (combinations of series and parallel) system (Der Kiureghian 2005, 2006). For example, consider a system event consisting of components, each of which has two states. The occurrences of the binary states of the th component are denoted and . Each component event is generally represented by a limit state function the inputs of which are random variables describing uncertain resistance and load effects (Melchers and Beck 2018). In general, the failure event is represented by the negative sign of the corresponding limit state function , and thus the component failure probability can be formulated aswhere = probability of event; = joint probability density function (PDF) of ; and = -domain describing event , i.e., .
(1)
SSR problems for Boolean events aim to compute the probability of the system eventwhere = logical function consisting of unions and/or intersections of component events. The simplest forms of the systems include a series system characterized by the unions of eventsand a parallel system expressed as the intersections of events
(2)
(3)
(4)
A more complex form of the systems can be obtained by mixing series and parallel systems, i.e., cut-sets and link-sets (Der Kiureghian 2005; Thoft-Christensen and Murotsu 2012) which are described, respectively, aswhere and = failure of the cut-set system and survival of the link-set system, respectively; = index set of components in the th cut-set the joint failure of which constitutes system failure; and = index set of components in the th link-set the joint survival of which guarantees survival of the system. SSR problems can be formulated as
(5)
(6)
The estimation of the probability of these systems is not straightforward, especially when there are many components or the component events are statistically dependent. They often involve calculations of bi- and higher-order joint failure probabilities, which may require computationally demanding or infeasible multidimensional integrals. Therefore, to overcome these challenges, advanced system reliability methods have been developed over conventional approaches (Fussell 1975) for applications to general SSR problems.
Time-Invariant System Reliability Analysis Methods
Of various systems described by Boolean events, time-invariant system reliability problems are discussed in this section. The definition of a time-invariant system is that its random variables or component states do not vary over time (Melchers and Beck 2018). The discussion mainly focuses on addressing the statistical dependence and the logical operations of multiple components in a system with an affordable computational cost.
Methods for Parallel or Series Systems
Analytical (Non-Simulation-Based) Methods
Analytical (non-simulation-based) methods include approximation methods and bounding formulas that do not rely on Monte Carlo simulation (MCS). They often have high computational efficiency in small to midsize problems. Their implementation may involve complex procedures compared with crude MCS and mostly rely on the availability of precalculated component reliabilities (Der Kiureghian 2005).
Kounias (1968) developed mathematical formulas to estimate the probability bounds of a series system. Hunter (1976) extended the formulation by deriving a linear upper-bound estimation formula for a series system event. In contrast to previous upper-bound formulas developed by Boole (1911) and Bonferroni (1936), which used marginal probability information only, these bounding formulas use bicomponent probability information as well to achieve narrower bounds. Ditlevsen (1979b) derived theoretical formulas to compute lower and upper bounds using marginal and bicomponent probabilities. These developments led to the widely used Kounias–Hunter–Ditlevsen (KHD) boundswhere = marginal probability of component event , where ; and = bicomponent probability, where . Zhang (1993) derived higher-order reliability bounds for a series system which can incorporate third-order and even higher-order joint failure probability information to obtain narrower bounds.
(7)
Hohenbichler and Rackwitz (1982) proposed the first-order multinormal (FOMN) method for a parallel system probability calculation. This method is based on the first-order approximation concept, in which a correlated standard normal space is transformed to the uncorrelated standard normal space. In this method, the multidimensional integral is decomposed successively into the product of marginal and conditional probabilities until its dimension becomes one in which the conditional probabilities are approximately linearized. Tang and Melchers (1986) further developed this method to the improved FOMN (I-FOMN), which evaluates the conditional probability using an asymptotic polygonal approximation. They also developed the generalized FOMN (G-FOMN), which evaluates the exact conditional probabilities to improve the accuracy of FOMN by slightly compromising computation efficiency. Pandey (1998) developed a fast approximation method called product of conditional marginals (PCM) for a multinormal integral, in which the multinormal integral is approximated by the products of one-dimensional normal integrals. The dimension of a multinormal integral is reduced by successively decomposing it into an ()-dimensional conditional probability multiplied by a one-dimensional probability. The conditional limit state function is linearized in each step through recursive calculations of two variables, i.e., a conditional fractile and a conditional correlation coefficient. The accumulation of the errors is small considering the computational simplicity of the method. To reduce the error accumulation of PCM in handling a highly reliable series system, Yuan and Pandey (2006) developed the improved PCM (I-PCM), which reformulates the bivariate normal probability term in the original PCM using an equivalent complementary bivariate series system probability term.
Table 1 compares the reviewed analytical (non-simulation-based) approaches in terms of their accuracy, computational efficiency, and efforts required for implementation.
| Methods | Accuracy | Efficiency | Implementation | Other remarks |
|---|---|---|---|---|
| Conventional bounding formulas (Kounias 1968; Hunter 1976; Ditlevsen 1979b; Zhang 1993) | Bound width becomes narrower as adding more joint probability terms. | Computation time quickly increases as more joint terms are included and the system size increases. Efficiency cannot be directly compared with that of numerical approaches. | Simple algebraic calculations in the theoretical bounding formulas. | — |
| FOMN, I-FOMN, and G-FOMN methods (Hohenbichler and Rackwitz 1982; Tang and Melchers 1986) | Results agree well with those by Monte Carlo simulation (MCS), but error is accumulated as more components are included in the calculation. | More efficient than MCS for systems with up to 50 components. Computational time exponentially increases as the number of components increases. | Methods require iterative linearization, minimization, and integration. | Based on the assumption that the random variables are jointly normal. |
| PCM and IPCM (Pandey 1998; Yuan and Pandey 2006) | Error accumulation is slower than FOMN-based methods. Method was demonstrated with examples with up to 50 components. | More efficient than FOMN-based methods. As an indication, for a 50-dimensional problem, with the same computer power, IPCM spent 0.8 s, PCM 0.05 s, and GFOMN 4.5 s, approximately. Computational time increases as the number of components increases. | No iterative linearization or minimization procedure. Instead, products of one-dimensional integrals are required. | Based on the assumption that the random variables are jointly normal. |
MCS-Based Methods
The implementation of MCS-based methods is relatively straightforward because the state of the target system event can be identified deterministically for each random sample. Logical operations such as union and intersection can be implemented simply by using min and max functions. Their computational cost often increases when the system failure is a rare event or when the desired precision level of the evaluated probability is high. To overcome these challenges in brute force MCS, advanced techniques have been developed for efficient evaluation of system reliability.
Ambartzumian et al. (1998) developed sequential conditioned importance sampling (IS). This method, which is based on the first-order concept (Hohenbichler and Rackwitz 1982), sequentially generates random samples based on the previous sample until a failed component is observed. Mori and Kato (2003) developed a method for series systems by proposing an optimal importance sampling function expressed as a weighted linear combination of linearized failure modes. The random sampling was carried out over a truncated normal PDF. Genz (1992) developed an efficient method based on three-step transformations from the multinormal integral to an integral over a unit hypercube to make the integrand simpler. The method enables a priority ordering of integration variables and makes the numerical integration more efficient. For numerical integration, three algorithms, the Schervish algorithm (Schervish 1984), MCS, and a subregion adaptive algorithm, were tested. The performance of the method was expedited further by adapting a randomized quasi-random rule with an optimized quasi-random integration point set, as demonstrated in software (Genz 2018). An importance sampling based technique for high-dimensional multinormal integral was developed by proposing an IS density containing all the components (Patelli et al. 2011). The methods reviewed in this subsection were developed mainly for multinormal probability calculations.
Table 2 compares the reviewed MCS-based approaches in terms of their accuracy, computational speed, and implementation details, and provides some remarks.
| Methods | Accuracy | Efficiency | Implementation | Other remarks |
|---|---|---|---|---|
| Sequential conditioned importance sampling (Ambartzumian et al. 1998) | Tested through numerical examples for the reliability index ranges 1–10 and up to 20 components while considering various correlation degrees. Mostly fewer than 1,000 samples are required. | Computational time is not significantly affected by the level of the probability and modestly increases with the number of components and the correlation between the random variables. | Conditional sampling is performed sequentially. | As byproducts, the method can provide the sensitivity of system probability with respect to distribution parameters and boundaries of domain. |
| Importance sampling for series systems (Mori and Kato 2003) | Method was tested through numerical examples for reliability indices of 1–5 and various correlation degrees. Up to 50 components were considered. The method showed better accuracy than G-FOMN and PCM. | Method is faster than MCS and twice faster than G-FOMN but slower than PCM, especially for problems with many components. For 50-dimensional problem, the proposed method was 3 times slower than PCM, 2 times faster than G-FOMN, and 50 times faster than crude MCS with samples. | Rotations of the coordinates of the samples are required for linearized limit states that are nonperpendicular to the sample space. | Method was developed for series systems. |
| Genz’s (1992) method | Method was tested through numerical examples for up to 20 component problems, but the accuracy is well kept even for higher dimension problems. Method is more accurate than other analytical methods. | Method is slower than other analytical methods, but the speed has been significantly improved by using a randomized quasi-random rule. | Implementation requires transformations of multinormal integrals and the Cholesky decomposition of a covariance matrix. | Error accumulation is remarkably low for parallel systems. |
| Importance sampling–based technique for parallel systems (Patelli et al. 2011) | Tested through numerical examples with up to 10 components with 50 random variables, and was more accurate than standard IS and PCM. | Efficiency is better than that of standard importance sampling because all unit vectors become orthogonal to each other. | Implementation requires the singular value decomposition, and sampling of each component is done independently from other components. | Method was further developed for slightly nonlinear limit states to handle non-Gaussian parameters. |
Methods for General Systems
This section reviews SSR methods directly applicable to general systems in Eq. (5), including series and parallel systems in Eqs. (3) and (4).
Analytical (Non-Simulation-Based) Methods
Hohenbichler and Rackwitz (1982) developed a bounding formula using the first-order concept. The multinormal integral in each cut-set and joint probabilities of cut-sets are approximated, and the union operation in the cut-sets is performed by applying the bounding formulas proposed by Hunter (1976) and Ditlevsen (1979b). Gollwitzer and Rackwitz (1983) developed an equivalent hyperplane concept, in which the reliability of a subsystem is represented by an equivalent hyperplane with a generalized reliability index (Ditlevsen 1979a). The correlations between subsystems are represented by their approximated directional cosine vectors. Murotsu et al. (1982) proposed an upper bound of the system reliability of a redundant frame structure. The approach automatically generates the failure modes, and dominant failure modes are identified systematically using the branch-and-bounds method.
Song and Der Kiureghian (2003) developed a method to obtain bounds on system reliability by linear programming (LP), often referred to as the LP bounds method, which can be applied not only to series, parallel, cut-set, and link-set systems, but also to any general systems. The narrowest bounds are obtained by solving the linear optimization problemwhere = set of probabilities of mutually exclusive and collectively exhaustive (MECE) events of the sample space, with which the probability of the target system event, , and the available information on the marginal and joint failure probabilities can be described as linear functions. In Eq. (8), the linear objective function describes the system failure probability . The equality- and inequality-type information of the marginal and joint failure probabilities are described by use of the matrices and and vectors and . Unlike theoretical bounding formulas, the LP bounds method can incorporate even an incomplete set of component probabilities and inequality constraints. A shortcoming is that the size of the LP problem grows exponentially with the number of components, which may result in a computer memory issue. To overcome this, a divide-and-conquer multiscale approach was proposed. The approach defines subsystems as supercomponents (Der Kiureghian and Song 2008) and obtains bounds of their marginal and joint probabilities using the LP bounds method. Next, these are used as the constraints for the LP problem defined for the target system event. Byun and Song (2020) proposed an LP bounds method with delayed column generation, which can alleviate significantly the memory requirement by an iteration of smaller binary integer programming.
(8)
Approximation methods have been developed for a point estimation of system reliability. Kang et al. (2008) and Song and Kang (2009) developed the matrix-based system reliability (MSR) method to estimate the reliability of general systems and its parameter sensitivities. In this method, system reliability is calculated by [Eq. (8)], i.e., the product of the two vectors, the event vector and the probability vector . The event vector can describe any general events by using the proposed vector operations, whereas the probability vector is expanded sequentially to represent all MECE events in the system space. The statistical dependence between components is handled by identifying a common source random variable (CSRV) to utilize conditional independency of the component events given an outcome of CSRV. For the case in which CSRVs are not identifiable directly in a given problem, the Dunnett and Sobel (1955) model was generalized and fitted with the given correlation matrix (Song and Kang 2009). The MSR method was developed further by Kang et al. (2012) for efficient evaluation of the integrals in the CSRV space using the first- or second-order reliability methods (FORM and SORM), and for the sensitivity of the system failure probability with respect to the parameters that affect the correlation coefficients between the components. Byun et al. (2017) extended the matrix formulation of the MSR method to solve -out-of- system problems in their efforts to evaluate the reliability growth of a complex system. The matrix-based formulation of the events and their corresponding probabilities in the LP bounds (Song and Der Kiureghian 2003) and MSR (Kang et al. 2008; Song and Kang 2009) methods led to the development of a matrix-based Bayesian network (MBN) (Byun et al. 2019), which utilizes an alternative matrix-based data structure of the probability mass functions for efficient memory storage and flexible inference.
Kang and Song (2010) developed the sequential compounding method (SCM) to approximate rapidly the reliability of general systems. This method compounds two components coupled by a logical function, i.e., union or intersection, successively until the whole system becomes a single supercomponent. Efficient approximation procedures were proposed to estimate the reliability index of the supercomponent and its correlation coefficient with the remaining components. Chun et al. (2015) proposed a method to calculate the system reliability sensitivity with respect to design/input parameters using SCM. The SCM was applied to first-passage probability–based design and topology optimization of structures (Chun et al. 2019b), in which the parameter sensitivities of general system reliability are required. Roscoe et al. (2015) developed the equivalent planes methods, which iteratively express a two-component system as an equivalent plane. This method differs from SCM in that it uses the information of the autocorrelation of all the underlying random variables instead of the correlation between the components.
Table 3 compares the analytical methods for general system reliability estimation reviewed in this section in terms of their accuracy, efficiency, and implementation, and provides other remarks.
| Methods | Accuracy | Efficiency | Implementation | Other remarks |
|---|---|---|---|---|
| Bounding formulas (Hohenbichler and Rackwitz 1982; Gollwitzer and Rackwitz 1983; Ditlevsen 1979b, Murotsu et al. 1982) | Bound width becomes narrower by adding more probability terms. Bounds become wider as the number of components in the system increases. | Rapid computation for a small system. Computation time quickly increases as more joint terms are included and the system size increases. | Methods require simple and straightforward calculations but need to deal with many terms for high-dimensional problems. | Methods rely on cut-set formulations or the branch-and-bound method. |
| LP bounds method (Song and Der Kiureghian 2003; Der Kiureghian and Song 2008; Byun and Song 2020) | Method provides the narrowest possible bounds for the given joint probability information. Method was demonstrated through applications to structural systems with redundancy. | Vector size increases exponentially with the number of components, which may result in issues related to computational time and memory. Multiscale approach or alternative optimization algorithms can alleviate this issue. | Linear programming needs to be implemented. | Method provides byproducts such as system reliability–based importance measures and sensitivities. Incomplete and inequality information on the component probabilities can be incorporated for narrower bounds. |
| MSR (Kang et al. 2008; Song and Kang 2009; Kang et al. 2012; Byun et al. 2017) | Error mainly arises from the generalized DS model fitting of the correlation matrix. Method was demonstrated through a variety of examples including a bridge network, a bridge system, and redundant truss problems. | Vector size issue in the LP bounds methods in inherited. Multifold integration over CSRVs increases the computation time. However, the formulated event and probability vectors can be recycled to improve efficiency. | Matrix formulations and operations are required. Numerical integration over the space of CSRVs is needed. | Method provides byproducts such as system reliability–based importance measures and sensitivities. When involving incomplete information, MSR becomes the LP bounds method. |
| SCM (Kang and Song 2010; Chun et al. 2015) | Error accumulation is very small compared to other methods such as PCM, IPCM, and MSR. Method was demonstrated through general system problems with up to 1,000 limit states and various correlation structures. | Computation time increases as the number of components increases, but still is highly efficient especially for parallel or series systems. It was tested in general systems with as many as 1,000 components. As an indication, a 50-dimensional problem required 11.90 s using MATLAB version R2008a on a personal computer with an AMD dual-core 2.0-GHz processor. | Proposed compounding procedures need to be applied sequentially. | Method provides byproducts such as the system reliability–based importance measures and sensitivities. |
| Equivalent planes method (Roscoe et al. 2015) | Error accumulation is small for up to 650 components. Error incurs when combining components. Accuracy is affected by the number of random variables and the correlation level. | For a general system with 250 components with the reliability index of 5, the computation times of directional MCS and the method were 17 h and less than 1 s. | Linearization procedures are performed iteratively. | Method is different from SCM because it needs autocorrelation of all underlying random variables instead of correlation of the components. |
MCS-Based Methods
Kurtz and Song (2013) proposed the Kullback–Leibler cross entropy–based adaptive importance sampling using Gaussian mixture (CE-AIS-GM) by further developing the cross entropy–based adaptive importance sampling method (CE-AIS) (Rubinstein and Kroese 2013). The method effectively finds a near-optimal importance sampling density with a few rounds of sampling. This is achieved by minimizing the difference between the best importance sampling density and the Gaussian mixture model, which is measured by the cross entropy. Wang and Song (2016) further developed CE-AIS-GM for component and system reliability problems in high-dimensional space using von Mises–Fisher mixture (CE-AIS-vMFM). Jiang et al. (2017) adopted the subset simulation developed by Au and Beck (2001) for the purpose of SSR analysis by using a system limit state function, in which the logical functions are treated deterministically using min and max functions.
Bourinet et al. (2011) proposed the algorithm, which combines the subset simulation and the support vector machines (SVMs) with an active learning process, in which an SVM classifier is built successively for each of the intermediate limit states. Fauriat and Gayton (2014) developed an SSR analysis method based on active learning and kriging–based Monte Carlo simulation (AK-MCS) (Echard et al. 2011). AK-MCS generates brute-force MC samples and evaluates the limit state function for a small subset to train a kriging model, which is used to choose the next MC samples in which the limit state function is calculated. This active learning process relies on a merit function that quantifies the expected merit of choosing each of the MC samples as the next simulation point. AK-SYSi is an improved version of AK-SYS specifically for the composite criterion approach by proposing a refined learning function to avoid false identification of failure modes (Yun et al. 2019). Hu et al. (2017) proposed the efficient kriging surrogate modeling approach (EKSA) for SSR analysis by using a composite surrogate built upon individual component and singular value decomposition (SVD) to efficiently represent the high-dimensional correlated vectors (Palmer et al. 2012). For further development of this method, inclusion of epistemic uncertainty and extension to time-varying reliability analysis could be considered. The adaptive kriging-oriented importance sampling (AKOIS) method was proposed for multiple most probable failure points problems. The method used a double-loop algorithm to identify importance sampling centers and subregion centering for samples (Zhang et al. 2020). Many MCS-based methods potentially have general applicability to system reliability analysis. However, because they were mainly developed for a single limit state, further challenges and issues could arise in their application to system reliability analysis, such as selection of seeds and samples, and surrogating multiple limit states. Therefore, this review focused on MCS methods and algorithms developed specifically for system reliability analysis.
Table 4 compares the simulation-based methods for general systems in terms of their accuracy, efficiency, and implementation.
| Methods | Accuracy | Efficiency | Implementation |
|---|---|---|---|
| CE-AIS–based methods (Kurtz and Song 2013; Rubinstein and Kroese 2013; Wang and Song 2016) | CE-AIS-GM performs better than CE-AIS-SG in series systems. Accuracy is not sensitive to probability level, random variable dimension (up to 50), or limit state nonlinearity. | For problems in which MCS requires about samples, CE-AIS-GM and CE-AIS-SG reduce the required number of samples to about . Required number of samples is not affected by the level of probability. | Optimization process is required to obtain near-optimal density in importance sampling. |
| Subset simulation–based SSR method (Jiang et al. 2017; Au and Beck 2001) | Accuracy was demonstrated through problems with on the order of probabilities, and the accuracy was agreeable to MCS. It was demonstrated through system problems with on the order of probabilities. Method showed better accuracy than the equivalent component concept–based method. | For probabilities lower than , the method is much faster than MCS. As an indication, for a problem with a probability of , the proposed method was 500 times faster than crude MCS. However, for probabilities greater than , MCS and subset simulation had similar speed. | Implementation of subset simulation is required, in which min and max functions are used to describe the system definition. |
| AK-SYS (Fauriat and Gayton 2014) | Method was validated through parallel and series systems. Method had less than 1% error, up to 10 limit states with 11 random variables. Method was more accurate than the direct use of AK-MCS. | In a tested example, fewer than 50 samples were needed, whereas MCS used samples. | Active learning process needs to be implemented with the learning functions developed for system limit states. Number of the initial design of experiments needs to be chosen based on experience. |
| AK-SYSi (Yun et al. 2019) | Tested for up to 10 failure modes with 11 random variables. | Had faster convergence than AK-SYS. As an indication, almost half the total number of function calls were required in the examples. | Refined learning function is implemented on top of AK-SYS. |
| Kriging surrogate approach (Hu et al. 2017) | Accuracy of the method is similar to that of AK-SYS and higher than AK-MCS. Method was verified through an 8-limit state series system, a 9-limit state parallel system, and a 5-limit state general system with up to 11 random variables. | Method required slightly fewer samples than AK-SYS and much fewer than AK-MCS. As an indication, for a problem with a probability of for which the proposed method and AK-SYS required 30–40 samples, MCS used samples to obtain similar results. | As the number of components increases, more surrogate models need to be constructed for individual limit states. |
| AKOIS (Zhang et al. 2020) | Numerical examples and a steel frame structure example consisting of several limit states or multiple most probable failure points were considered. As an indication, in the structural example, the accuracy was similar to that of AK-MCS and comparable to that of MCS. | As an indication, in the structural example, AKOIS required 5% of the number of finite-element calls required by AK-MCS. | Implementation requires double-loop active learning procedures. |
Time-Variant System Reliability Analysis Methods
This section reviews time-variant system reliability analysis methods, in which the system has time-varying random variables or component states. The review focused on methods developed specifically for time-variant reliability analysis of systems. Mahadevan and Xiao (1995) proposed a failure path approach for time-variant reliability estimation for brittle structures in which significant failure sequences were identified using the branch-and-bound method. The Markov chain assumption is used to model the cumulative damage due to time-varying loads with the Poisson process, and the overlapping load effect is considered. Enright and Frangopol (1998) proposed a Monte Carlo–based method for system reliability estimation for a deteriorating structure with deteriorating resistance and two independent time-variant (live) and invariant (dead) loads modeled based on Mori and Ellingwood (1993a, b). The system events are represented by event trees, and the system reliabilities are calculated using an adaptive importance sampling technique (Enright 2000). Enright and Frangopol (1999) applied this approach to an RC bridge suffering corrosion while considering the effect of resistance degradation.
Der Kiureghian et al. (2007) derived closed-form expressions for the mean rates of failure, the mean duration of repair, and the lower-bound time-variant system reliability of a minimal cut-set system with randomly and independently failing components. Song and Der Kiureghian (2006) introduced a notion of the joint first-passage reliability to promote the use of first-passage probabilities in reliability analysis of a system the components of which are subjected to common stochastic excitations. Approximation formulas for calculating a joint first-passage probability for two and three correlated stationary and zero-mean Gaussian vector processes were proposed by expanding the Poisson (Rice 1944, 1945) and Vanmarcke (1975) approximations available for marginal first-passage probabilities. These were applied to compute the bounds of the failure probability of an electrical substation network subjected to earthquake excitations through integration with the LP bounds method (Song and Der Kiureghian 2003). Gupta et al. (2006) developed a method for series systems with statistically correlated log-normal vector responses. The main assumption was that for high crossing thresholds, the number of level crossings of a non-Gaussian process could be modeled as a Poisson point process; however, this was a source of error and inaccuracy.
Son and Savage (2007) proposed a reliability estimation approach for multiple time-variant responses due to component degradation for discrete time points. Series systems are considered, the system reliability is calculated using the second-order bounds, and FORM is used for the joint probability calculations. Sonal et al. (2018) proposed a variance reduction scheme using the subset simulation and the Markov chain splitting (Kanjilal and Manohar 2015), in which the interim levels in the subset simulation are fixed and not subjected to the sampling fluctuations, and the simulations in each level can be performed independently. The method achieves a similar level of coefficient of variation (COV) as other subset sampling–based studies (Au and Beck 2001; Pradlwarter et al. 2007). Yu et al. (2018) proposed an approach to calculate the time-variant reliability for multiple failure modes and temporal parameters based on the extreme value moment method and the improved maximum entropy method. The maximum entropy method estimates a PDF based on high-order extreme moments and the extreme value moments by using the sparse grid technique to overcome the curse of dimensionality and the extreme value theory. Lu et al. (2018) proposed an event tree and -unzipping (Thoft-Christensen and Murotsu 2012) based method. This approach expedites the reliability analysis process by using the adaptive support vector regression to construct response surface functions. Du et al. (2019) proposed a parallel subset simulation–based method, which can be applied to problems with multiple limit states. The concept of a principal variable that is correlated with all limit states was proposed to generate samples in the analysis for multiple Gaussian and non-Gaussian stochastic processes. The principal variable is determined using the principal component analysis based on the Pearson correlation coefficient.
Table 5 compares the time-variant system reliability methods in terms of their assumptions about the component level processes and the time-invariant methods adopted by the methods.
| Methods | Assumption for component level time-variant process | Time-invariant system reliability analysis method adopted | Other remarks |
|---|---|---|---|
| Markov chain–based model (Mahadevan and Xiao 1995) | Poisson process with a Markov chain model is assumed. | Branch-and-bound method. | — |
| MCS-based time-invariant SSR approach (Enright and Frangopol 1998) | Poisson process for load and a degradation model for resistance. | Event tree and an adaptive importance sampling. | — |
| Bound formulas for systems with randomly failing, repairable components (Der Kiureghian et al. 2007) | Homogeneous Poisson process and exponentially distributed repair durations are assumed. | Closed-form expressions. | Method is applicable to statistically independent components. Method also provides importance measures and sensitivities. |
| Joint first-passage reliability method (Song and Der Kiureghian 2006) | Stationary zero-mean Gaussian vector process is assumed. Poisson and Vanmarcke approximations were developed to consider dependency. | LP bounds method (Song and Der Kiureghian 2003). | Method was verified against MCS results. |
| Method for series systems with a log-normal vector response (Gupta et al. 2006) | Number of level crossings of a non-Gaussian process is modeled as a Poisson point process. | Analytical formulations. | Proposed multivariate extreme value distributions have limitations and inaccuracies due to the Poisson point process assumption. |
| FORM and set theory–based method (Son and Savage 2007) | Discrete time intervals are assumed. | Second-order bounds and FORM concept for joint probability calculations. | — |
| Variation reduction scheme using subset simulation (Sonal et al. 2018) | Excitation is assumed to follow a zero mean non-stationary Gaussian process. | Subset simulation and Markov chain splitting. | Method is faster than crude MCS for small probability estimations of less than . |
| Extreme value moment and entropy method (Yu et al. 2018) | Extreme value distribution is assumed based on discrete time points. | Extreme value moment and entropy method. | — |
| Event tree and -unzipping–based method (Lu et al. 2018) | Discrete time interval was assumed, and the resistance degradation model was used. | -unzipping method and support vector machine. | — |
| Parallel subset simulation–based method (Du et al. 2019) | Gaussian and non-Gaussian processes are transformed into discrete time points and independent static limit states. | Parallel subset simulation. | — |
SSR Methods for Sequential Failures
Introduction
Various types of structural systems are subject to the risk of sequential failures (Byers et al. 1997; Karamchandani et al. 1992). These structural systems should have a sufficient level of structural redundancy so that the failures of structural components (hereinafter referred to as members) do not progress toward system-level failure such as collapse, which can cause serious structural damage and socioeconomic losses. To prevent such disastrous events, structural systems should be designed and maintained based on accurate SSR analysis with the risk of sequential failure properly considered.
A challenge in such SSR analysis is that the definition of system-level failure is not determined a priori, but rather is identified through repeated structural analyses following an event tree of potential failure sequences (Lee and Song 2011). This means that, for a complex structural system, one might need to explore a large number of member failure sequences in order to obtain an accurate estimate of system reliability. Furthermore, calculating the probability of each failure sequence requires component and system reliability analyses in conjunction with sophisticated structural analysis, because the effects of various sources of uncertainty and load redistributions during sequential failures need to be considered (Lee and Song 2012). Thus, SSR analysis taking into consideration sequential failure often involves overwhelming computational cost and time.
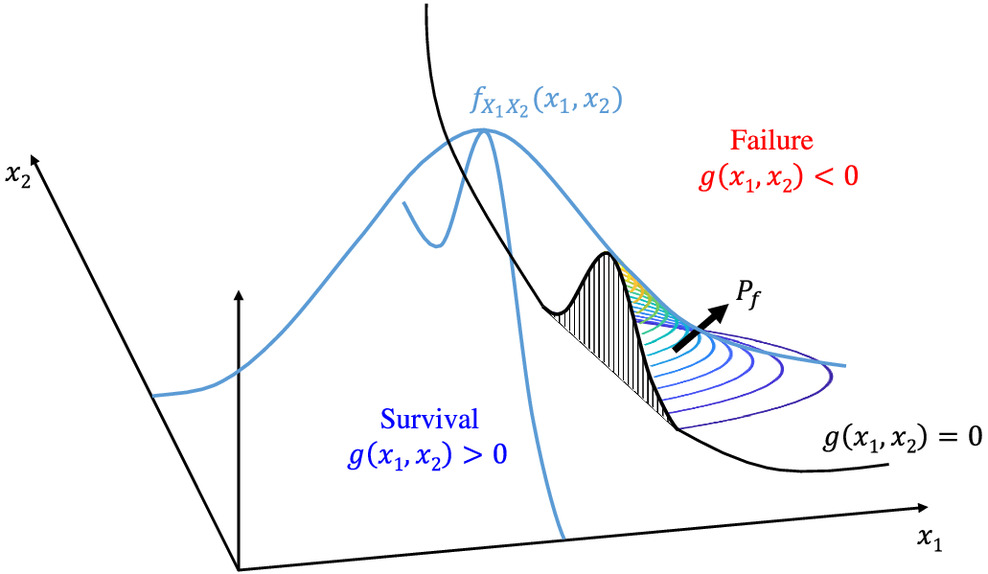
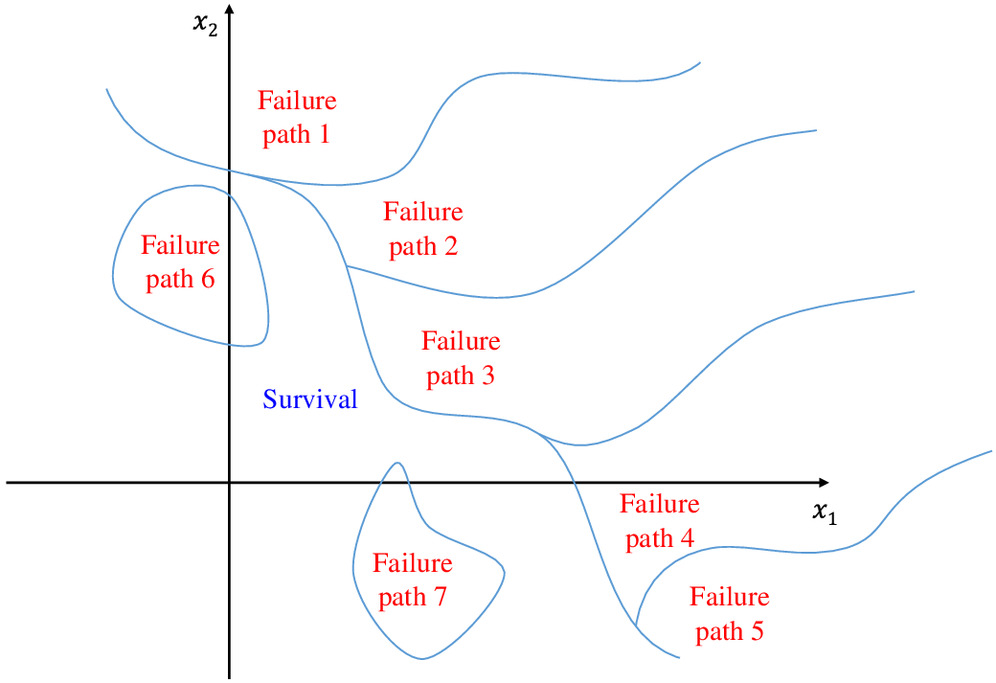
For example, when two random variables are used to describe a structural reliability problem in Eq. (1), the failure probability can be illustrated as in Fig. 1. The failure and survival (i.e., nonfailure) domains are separated by , i.e., the limit state surface, and the failure probability is equal to the volume of the joint PDF over the failure domain . If the reliability (or failure probability) of a structural member is of interest, the failure domain often is constituted with a single region, and the limit state function is smooth and not highly nonlinear.
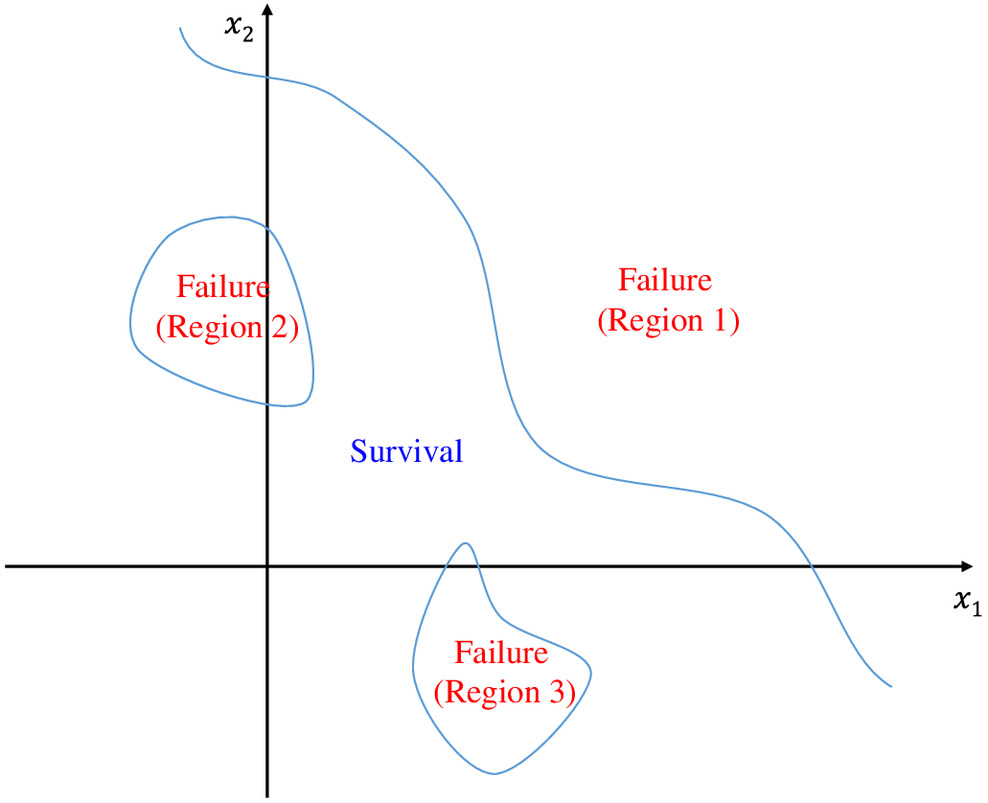
On the other hand, when a structural system subject to sequential failures is of interest, the system failure domain in Eq. (6), i.e., , is often constituted of multiple regions (Fig. 2). In Fig. 2, each region represents a sequential failure; for example, Member B fails under the load condition caused by the preceding failure of Member A, or Member C fails under the load condition caused by the preceding failures of Members A and B (Kim et al. 2013). The limit state surfaces separating the failure and survival domains may be highly nonlinear, which makes the problem more challenging. Another important challenge is that, after a member fails, the limit state functions of the remaining members should be redefined because of the effect of the failure, such as the load redistribution. As a result, the required number of limit state functions and component reliability analyses increases exponentially, which may lead to a computationally intractable SSR problem.
This section comprehensively reviews SSR methods that have been developed to address these technical challenges regarding sequential failures of structural systems. The challenges caused by sequential failures are described, and a few existing SSR approaches along with their advantages and limitations are introduced.
Numerical Approaches
Analytical Formulation–Based Methods
Several studies addressed challenges of SSR problems involving sequential failures by deriving analytical formulations. For example, Stahl and Geyer (1984) derived mathematical formulations to estimate the probability of fatigue-induced sequential failures for the Daniels (1945) system problem in which the reliability of a bunch of wires is investigated while considering the load-redistribution effects. The fatigue life was derived to follow a lognormal distribution. The correlations between structural members also were derived analytically. These analytical formulations made it possible to calculate the probability of a sequential failure event, and the failure probability of the Daniels system then was estimated. Although this method can provide an exact solution for the system reliability of a structural system with consideration of sequential failures, its application is limited to fatigue problems in parallel systems in which the random variables are assumed to follow lognormal distributions.
Some researchers modeled the problem using LP. For example, Ditlevsen and Bjerager (1984) expressed the failure of structural members as linear functions and calculated the system failure probability by solving the corresponding LP problem. The proposed method was applied to frame structures to obtain the lower and upper bounds of the system reliability. Bjerager (1989) also introduced the use of LP into modeling such SSR problems, and estimated the system-level reliability of truss structures. However, the application of these LP-based methods is limited to cases in which the failures of structural members are described by linear limit state functions, and the associated random variables are assumed to be normally distributed.
MCS-Based Methods
MCS (Rubinstein and Kroese 2016; Shinozuka 1983), which involves repeating computational simulations for many scenarios based on randomly generated values of uncertain parameters (so-called samples), is advantageous in dealing with sequential failures because of its straightforward applications to general reliability problems. Some researchers have combined MCS-based methods with failure path algorithms to consider the order of failure events of structural members leading to system collapse. This failure sequence description helps to provide more accurate estimates of system reliability. This section introduces such efforts, with a focus on MCS. More details on failure path algorithms are provided in the section “Failure Path Approaches.”
Yang and Younis (2005) estimated the failure probability of a power plant system considering the load redistribution that may occur during sequential failures. They calculated the probabilities of component events constituting a failure path using FORM and SORM (Der Kiureghian 2005), and estimated the system failure probabilities using MCS. Similarly, Dey and Mahadevan (1998), Enright and Frangopol (1999), and Mahadevan and Raghothamachar (2000) employed adaptive importance sampling and a failure path approach to calculate the system failure probabilities of a truss, frame, and concrete bridge, respectively. Mahadevan and Xiao (1995) used the failure path algorithm with the Markov-chain Monte Carlo (MCMC) method to estimate the system reliability of a truss.
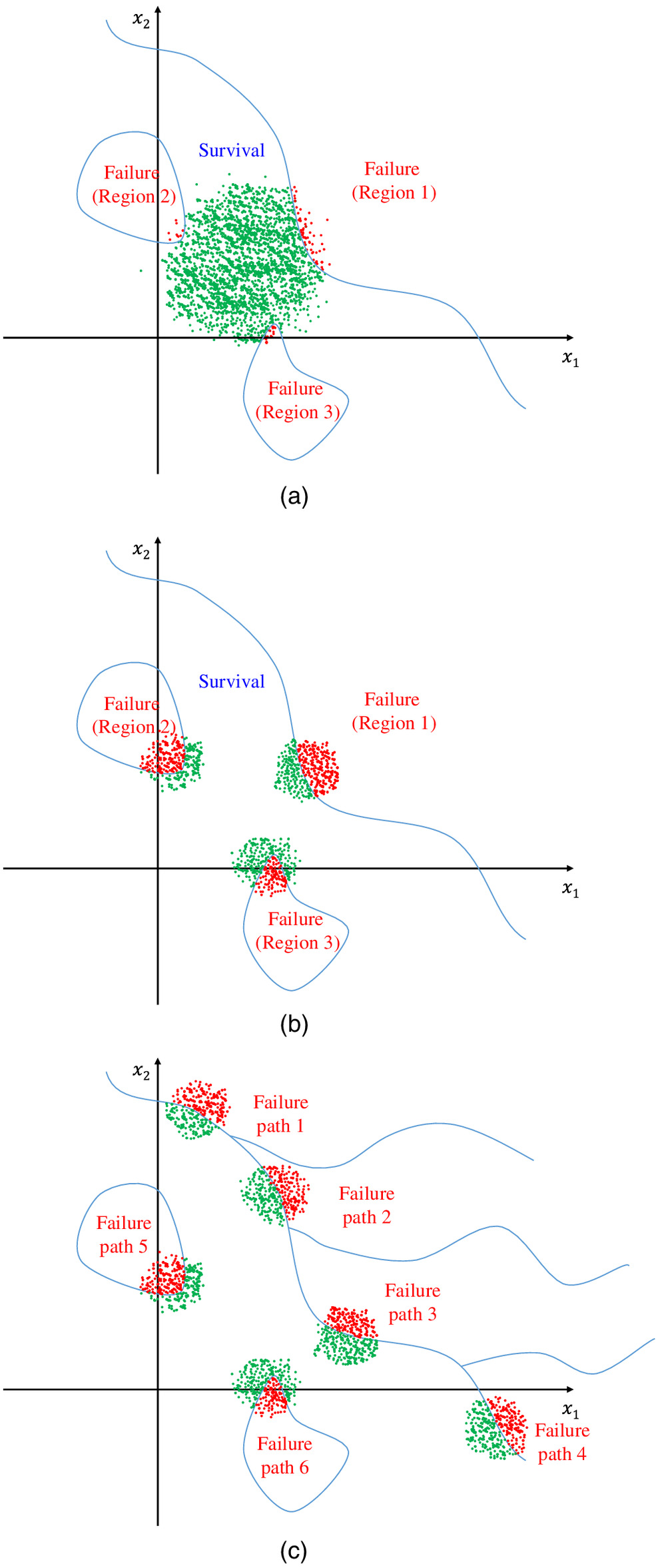
Fig. 3 illustrates the concepts of standard MCS, advanced MCS, and advanced MCS with the failure path algorithm. As mentioned previously, a standard MCS [Fig. 3(a)] may require a large number of samples and involve a huge computational cost because most of the randomly-generated samples are likely to fall within the survival domain, whereas a small number of samples are likely to fall within the failure domain. To resolve this issue and increase the efficiency of SSR analysis, various advanced approaches to MCS have been introduced and combined with failure path algorithms so that more samples can fall within the failure domain [Figs. 3(b and c)]. These advanced MCS-based methods have been applied successfully to various structural systems, such as trusses, frames, and bridges. However, application of such methods to more complex structural systems still involves considerable computational cost, so the computational efficiency of advanced MCS-based methods needs to be improved further.
Response Surface–Based Approaches
As mentioned in the section “Introduction,” a critical challenge in SSR analysis dealing with sequential failure is the high nonlinearity of the limit state surface representing the system failure event. To alleviate the issues caused by the nonlinearity, response surface–based methods have been employed. The response surface approach is a collection of statistical analysis methods that examine the relationship between experimental response and the values of input variables (Box et al. 1978; Draper and Smith 1998). Since its first development by research scientists in biology and agriculture, it has been applied to creating and analyzing statistical models of performance functions in structural reliability the direct investigation of which had been considered too difficult.
For example, Zhao and Ono (1998) estimated the system reliability of frame structures using the response surface method. They first approximated the system-level performance function of the target frame structure as a function of applied loads. After the response surface function was constructed, FORM (Der Kiureghian 2005) was applied to calculate the component and system failure probability. Similarly, Ghosn et al. (2010) used the response surface method to estimate the system reliability of highway bridges consisting of superstructures and substructures. Furthermore, based on the system reliability estimates, they proposed a probabilistic framework to quantify the structural redundancy and robustness of the bridges. Liu and Moses (1994) employed the response surface method to simplify the limit state functions for a three-bar truss and multiweb wing of an aircraft. For the simplified limit state functions, they used importance sampling to estimate the system reliability.
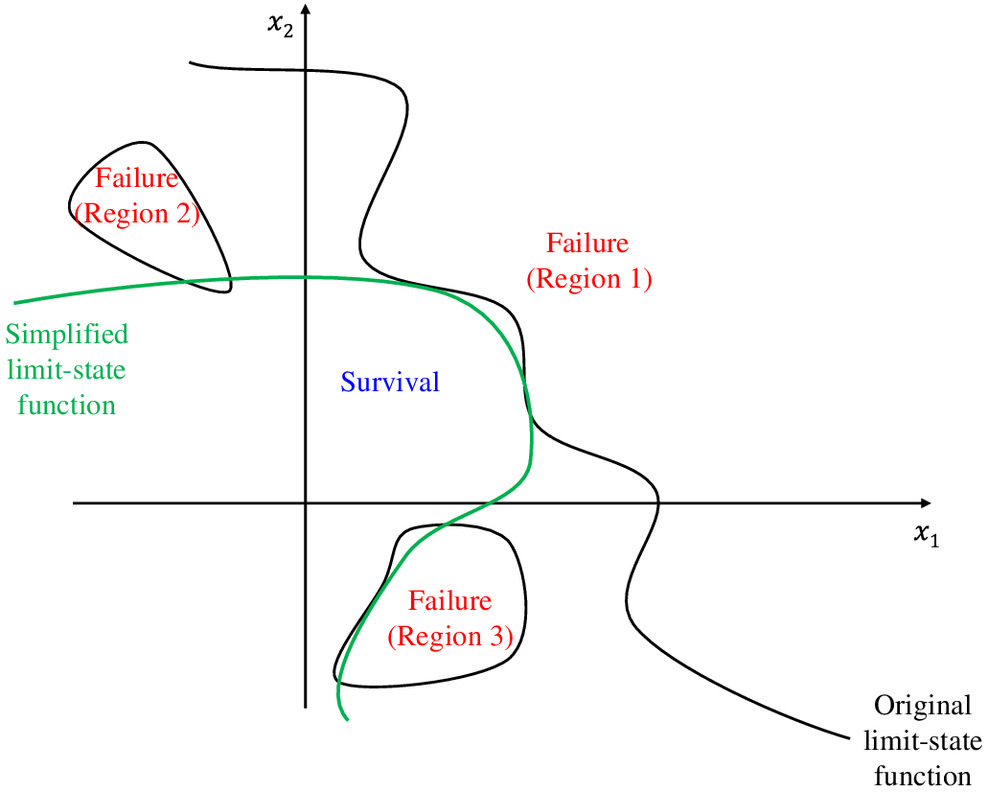
Fig. 4 illustrates the concept of the response surface method. Whereas the original limit state function representing the system reliability may be highly complex and nonlinear when considering sequential failures, the limit state function obtained using the response surface method can be relatively simple and not highly nonlinear. After the limit state function is simplified, the problem can be solved by conventional structural reliability methods such as FORM, SORM, or MCS (Der Kiureghian 2005). Several studies have shown that the response surface–based methods can provide good approximations of system reliability estimates (Ghosn et al. 2010; Liu and Moses 1994; Zhao and Ono 1998). However, the response surface–based methods may cause errors in reliability outcomes, mainly because of the simplification of the limit state function.
Failure Path Approaches
Another notable approach to deal with sequential failures in SSR analysis is a failure path algorithm, in which the system failure is described by sequences of member failures (Gharaibeh et al. 2002; Hendawi and Frangopol 1994). Fig. 5 illustrates the concept of the failure path approach. As mentioned previously, the failure domain of a structural system subject to the risk of sequential failures often is highly complex because there can be a large number of failure sequences. The failure path algorithm can divide the complex failure domain into several subdomains that are relatively simple. The methods developed earlier in this category did not consider the order of member failures in a failure path (i.e., the failure sequence). However, consideration of the order of member failures was found to produce more accurate results. Such methods can be categorized into three subgroups: (1) deterministic search; (2) probabilistic local search; and (3) probabilistic global search.
Deterministic Search
Failure path approaches are initiated by a deterministic search approach, which performs a deterministic structural analysis using the mean values of the random variables to identify a sequence of failures leading to structural collapse. The most representative method of deterministic search is the incremental load method (Moses 1977, 1982). This method identifies a failure mode by following a load path from initial component failure to system collapse, which leads to a linear equation describing failure. The method has been developed for use in identifying collapse mode expressions for large structural systems consisting of both ductile and brittle components. The method often utilizes existing structural analysis programs with incremental loadings and repeats structural analyses following the sequences of component failures. The array of different potential collapse modes is determined by a systematic strategy of examining changes in component utilization ratios following element failures. The analysis procedure is summarized as follows:
1.
analyze the intact structure for the given load;
2.
identify the first structural element to fail;
3.
reanalyze the structure with the failed component eliminated; and
4.
repeat Steps 2 and 3 until structural collapse occurs.
The deterministic approach is prone to missing critical failure sequences because the sequences identified by this approach are not necessarily the most probable ones. In addition, the deterministic search can identify only one failure path for a given load because the method relies on deterministic structural analysis. To obtain additional sequences, the values of some variables need to be modified, and the deterministic analysis must be repeated. For example, one can strengthen structural members involved in the identified sequence to search for additional failure sequences. For this reason, deterministic search may not be appropriate for use in probabilistic evaluation of the risk of sequential failures.
Probabilistic Local Search
This section deals with a probabilistic extension of the deterministic search in the section “Deterministic Search.” The first step is to identify the member that is most likely to fail in an intact structure. A new structural analysis model is constructed to reflect the damage or failure of the identified member. Through component reliability analysis using the model, the member that is most likely to fail under the damage scenario is identified. This process is repeated until a system failure such as collapse is observed.
One of the most representative methods in this category is the truncated enumeration method. For structural systems with nonlinear member behavior, the truncated enumeration method can be used to identify sequence-dependent failure modes (Melchers and Tang 1984; Tang and Melchers 1987). The method is derived from consideration of the exhaustive enumeration of the event tree containing all combinations of structural member failures. This is performed by imposing a truncation criterion to delete those modes of failure which would make a negligible contribution to the probability of total system failure.
Another widely used method in this category is the -unzipping method (Hashemolhosseini 2013; Lu et al. 2018; Thoft-Christensen and Murotsu 2012). This method first requires a component-level reliability analysis of each structural element, and selection of the minimum reliability index. Potential failure components with reliability index values within a specified interval then are identified. The initial system then branches into different subsystems, according to a system updating criterion, by removing the component that is identified to have failed. These procedures are repeated until the structure collapses or fails to satisfy a specified performance requirement. Finally, the reliability indexes of the identified components are combined into a parallel-series system that is similar to an event tree, whereby the system reliability can be eventually evaluated.
However, the sequences identified by a local search approach may not be the most critical sequences overall. For example, there may be a member with the failure probability that is lower than that of the most likely to fail member, but the conditional probability of structural collapse given its failure can be fairly high. This important sequence could be missed if a search scheme focuses on the most likely to fail members at each step.
Probabilistic Global Search
One of the most widely used probabilistic approaches for global search is the so-called branch-and-bound method (Guenard 1984; Lee and Song 2011; Murotsu 1984), which was introduced to identify critical sequences with significant likelihood in an efficient manner. Although many research efforts have developed risk analysis methods based on the branch-and-bound approach, these methods still remain either time-consuming or prone to missing critical failure sequences.
The branch-and-bound method is considered to be more accurate than the search methods introduced in the sections “Deterministic Search” and “Probabilistic Local Search.” To identify system failure sequences that globally are most likely to occur, the method compares the probabilities of all the failure sequences that have been investigated during the search process and assumes that the most likely sequence of further damage occurs. When the system failure of interest, such as structural collapse, is observed, the particular sequence is identified as a system failure sequence. Unless heuristic rules are employed to truncate apparently insignificant sequences, the branch-and-bound method can identify system failure sequences in the decreasing order of their probabilities. This makes it possible to terminate the search process without ignoring significant system failure sequences.
For example, Karamchandani et al. (1992) applied the branch-and-bound search to offshore platforms to identify important sequences of member failures and calculate the system-level failure probability in terms of a lower bound. In the analysis, the branch-and-bound search introduces more reasonable rules for the determination of structural collapse than do heuristic rules, and reduces the required number of failure sequences and the computational cost.
Although this selective search approach based on the probabilities of sequences helps to reduce the number of sequences to explore, one still might need to explore a large number of sequences to obtain a reliable estimate of the risk of structural system failure (Lee and Song 2011). This is due to the lack of reasonable criteria that would help terminate the search without underestimating the system failure risk. A structural system failure event often is described as the union of the identified system failure sequences. During a search process, one can obtain a lower bound of the system failure probability by means of a system reliability analysis that employs the identified failure sequences, which can be continuously updated as new failure sequences are identified. Because the upper bound usually is unknown, the trend of the lower-bound updates alone cannot provide accurate termination criteria. This is because the size of the updates of the lower bound caused by newly identified system failure sequences does not decrease monotonically, due to the statistical dependence between identified failure modes. This is the case even if the likelihood of identified sequences decreases monotonically. Therefore, a termination criterion based solely on the apparent convergence of the lower bound may underestimate the system risk. Furthermore, a new system reliability analysis needs to be conducted each time the lower bound is updated.
To overcome these challenges, a branch-and-bound method employing system reliability bounds, termed the method (Lee and Song 2011, 2012), was developed. As in other existing approaches based on the branch-and-bound method, the method employs a systematic search scheme in which branching and bounding are repeated (Fig. 6). Unlike other existing approaches, however, the method identifies disjoint failure sequences in order to (1) obtain both the lower and upper bounds of the system failure probability, (2) achieve a monotonic decrease in the updates of the lower bound as the search process proceeds, and (3) update both bounds of the system failure probability without performing additional system reliability analysis. The updated bounds provide reasonable criteria for terminating the branch-and-bound search without missing critical sequences or estimating the system-level risk inaccurately. The method was improved after its initial development and successfully demonstrated by applications to truss and continuum structures. However, applications of the method have been limited to the problem of fatigue-induced sequential failure. Further research is needed to extend its applications to general SSR problems with sequential failures.
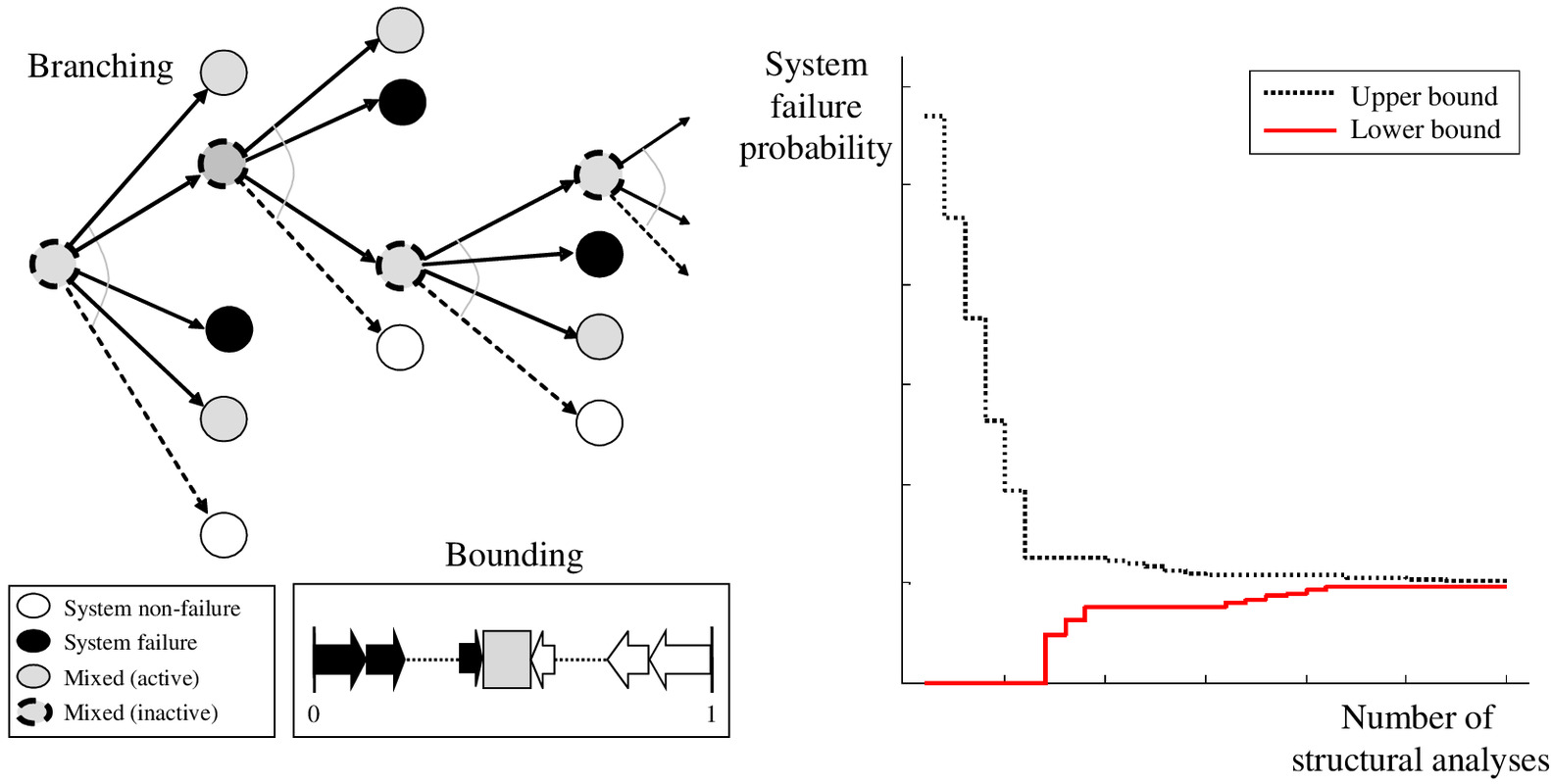
Another notable probabilistic global search is a selective search technique by Kim et al. (2013), which identifies sequential failure modes using a genetic algorithm. By identifying the domains representing sequential failures near the origin of the standard normal space with a priority, the method facilitates identifying those with dominant contributions to the system failure probability. The probabilities of the identified modes are calculated by the MSR method (Kang et al. 2008, 2012; Song and Kang 2009). This method was applied to complex offshore structural systems (Coccon et al. 2017) through combination with multiscale MSR analysis.
Table 6 compares the SSR methods reviewed in this section in terms of their implementation, efficiency, and accuracy, and provides other remarks. Direct comparison of these methods is challenging, and may not be reasonable because the associated problems differ in terms of the aspects of structural types, level of structural complexity, failure modes and definitions, and statistical modeling of random variables. More attention should be paid to the ongoing and further improvement of these methods, which is related closely to the development of SSR methods for Boolean system events (section “SSR Methods for Boolean System Events”).
| Approach | Implementation | Efficiency | Accuracy | Other remarks |
|---|---|---|---|---|
| Analytical formulation–based methods (Bjerager 1989; Ditlevsen and Bjerager 1984; Stahl and Geyer 1984) | Requires deriving analytical formulations representing sequential failures based on prescribed assumptions. | Mostly high because the formulations are derived in a way reducing computational costs. | Depends on the adequacy of prescribed assumptions in representing reality. | Prescribed assumptions include lognormal random variables and linear limit state functions. |
| MCS-based methods (Dey and Mahadevan 1998; Enright and Frangopol 1999; Mahadevan and Raghothamachar 2000; Mahadevan and Xiao 1995; Yang and Younis 2005) | Repeated computational simulations for many scenarios based on randomly generated samples. | Computational cost can be extremely large, especially when the expected level of system failure probability is low. However, it can be improved by using advanced MCS-based methods. | Accurate if enough number of samples is used. | Methods can be combined with failure path methods to increase the accuracy and efficiency of the analysis. |
| Response surface–based methods (Ghosn et al. 2010; Liu and Moses 1994; Zhao and Ono 1998) | Requires constructing a response surface function to approximate the system-level limit state function of sequential failures. | Mostly efficient because, compared with the original limit state function, it is cheaper to evaluate the constructed response surface function. | Depends on the accuracy of the constructed response surface function. | After the response surface is constructed, conventional methods of reliability analysis can be used to calculate the probability approximately. |
| Deterministic search (Moses 1977, 1982) | Performs a deterministic structural analysis using the mean values of random variables. | Compared with other failure path methods, computationally efficient because the method identifies only one failure path. | Accuracy of solutions cannot be checked or compared because the method is not probabilistic. | Because the method is not probabilistic, it may not be appropriate for the risk assessment of sequential failures. |
| Probabilistic local search (Hashemolhosseini 2013; Lu et al. 2018; Melchers and Tang 1984; Tang and Melchers 1987; Thoft-Christensen and Murotsu 2012) | Identifies the locally most likely to fail member repeatedly through component reliability analyses until a system failure is observed. | Similar to MCS-based methods, especially when the system failure is dominated by a few sequential paths and the expected level of system failure probability is low. | Compared with MCS-based methods, the accuracy of solutions can be high despite the reduced cost. | Prone to missing the most critical failure paths because the method focuses only on the most likely to fail members in each step. |
| Probabilistic global search(Coccon et al. 2017; Karamchandani et al. 1992; Kim et al. 2013; Lee and Song 2011, 2012) | Requires repeated identification of the globally most likely to fail member through component reliability analysis until a system failure is observed. | Search method is slower than the probabilistic local search but can be faster than MCS, especially when the system failure is dominated by a few sequential paths and the expected level of system failure probability is low. | Considered more accurate than other failure path methods, and the achieved upper bound on system reliability is fairly close to the exact solution. | Methods were originally developed for fatigue-induced sequential failures, and their application still is limited. |
SSR-Based Design/Topology Optimization
Introduction
Mathematical design optimization (Peressini et al. 1988; Haftka and Gu¨rdal 1992) aims to optimize design solutions with an objective function described in a mathematical form. The optimization problem may include constraints with regard to the structural performance or other criteria leading to feasible designs. The overarching goal of optimization is to identify a design solution that provides the best performance in terms of the prescribed objective function while satisfying given design constraints.
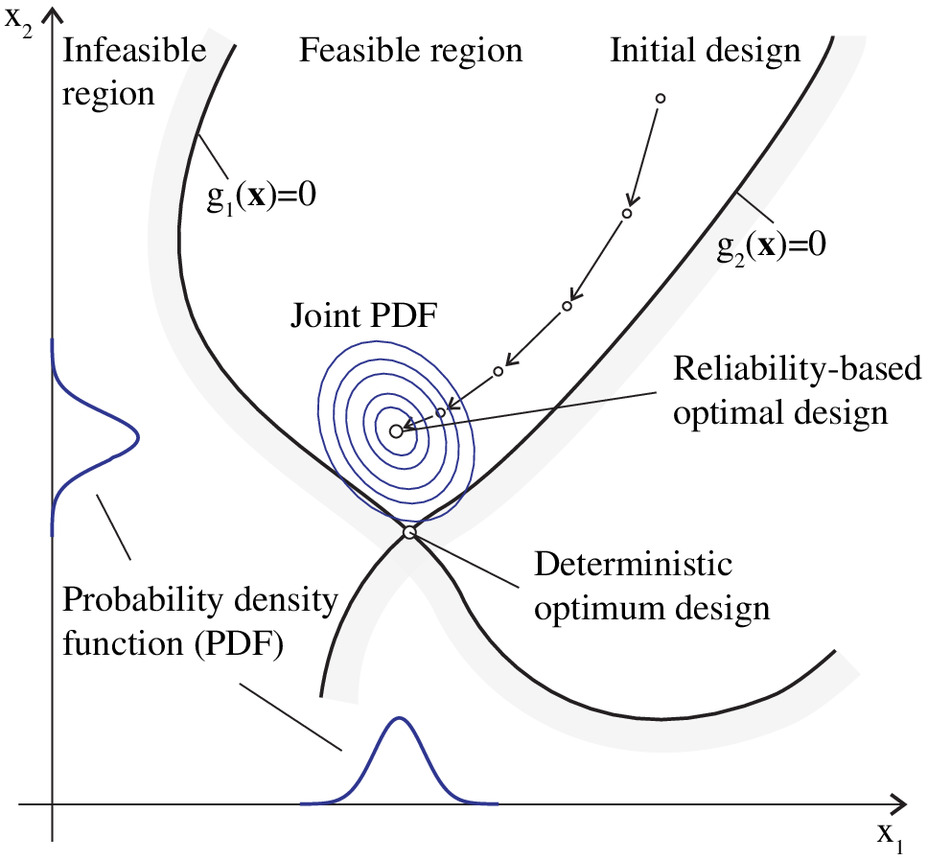
Deterministic optimization (DO) in engineering problems considers design parameters such as material properties, loadings, and geometry as deterministic quantities in analysis and optimization. However, consideration of uncertainties in loads and material properties is an essential aspect of engineering optimization because they can result in unexpected failures in components or systems, which eventually may lead to catastrophic damage and/or loss of life and assets. A design optimization process incorporating reliability analysis to constraints or the objective is referred to as reliability-based design optimization (RBDO) (Enevoldsen and Sørensen 1994; Frangopol et al. 1997; Frangopol and Maute 2004; Ayyub et al. 2015). Topology optimization (TO) (Bendsøe and Sigmund 2004) is a mathematical method that identifies the optimal shape of a structure by acting on its topology, in which the design variable is the material density in a continuum setting or a cross-sectional size in a discrete setting. In general, TO aims to achieve the best physical size, shape, and connectivity through material layouts obtained by the optimization procedure. TO has been applied successfully to various fields such as mechanical engineering (Schramm et al. 2002; Paulino and Silva 2005; Carbonari et al. 2007; Sigmund 2009), aerospace engineering (Krog et al. 2004), the medical field (Sutradhar et al. 2010), and structural engineering (Neves et al. 1995; Huang and Xie 2008; Stromberg et al. 2012; Chun 2016). Reliability-based topology optimization (RBTO) incorporates uncertainties into the TO process to generate the optimal topology while achieving a prescribed level of reliability.
In system reliability–based design/topology optimization (SRBDO/TO), the probabilistic constraint encompasses all the component failure events, which often are statistically dependent. The general concept of SRBDO/TO is illustrated in Fig. 7. The system-level optimization problem generally includes multidimensional integration for reliability analysis, complex sensitivity calculations for gradient-based optimization algorithms, and additional computational procedures to assess the system-level reliability. In recent decades, various studies and advancements in the field have overcome computational challenges and achieved accurate assessment of system reliability and sensitivity with regard to SRBDO/SRBTO. This section provides an overview of recent developments and future perspectives of SRBDO/SRBTO.
Mathematical Descriptions of Structural System Reliability–Based Optimization
System Reliability–Based Design Optimization (SRBDO)
RBDO problems typically are formulated with an objective function and deterministic and/or probabilistic constraints. Examples of the use of the objective function in RBDO include minimizing the failure probability of a structural system, minimizing cost or weight, and maximizing the structural performance. Design considerations, requirements, or other needs can be imposed in the form of constraint functions including probability terms. For a mathematical description of RBDO, consider design variables and random variables included in the objective and/or constraint functions. It is assumed that the design variables can be controlled to minimize or maximize the objective function throughout the optimization process. In the literature, the mean vector of selected random variables often is included as a design variable when the design optimization process can control the mean of the random variables.
A structural system typically is designed with a level of redundancy and fails as a result of the occurrence of multiple failure events or their combined effects. The failure domain for the system failure can be described aswhere = index set which includes elements of the th cut-set. The cut-set formulation in Eq. (9) can cover series and parallel system events in Eqs. (3) and (4) as well. Alternatively, the link-set formulation in Eq. (5) can be used to define the failure domain. Incorporating the system failure domain in Eq. (9) into the reliability constraint, SRBDO can be formulated. For example, the SRBDO formulation of a linear structure under static loads iswhere , , and = global stiffness matrix, displacement vector, and load vector, respectively; = system failure probability; = target failure probability; denotes the th component limit state function whose negative value indicates occurrence of failure; and and = lower and upper bounds of design variables, respectively.
(9)
(10)
System Reliability–Based Topology Optimization (SRBTO)
Topology optimization (Bendsøe and Sigmund 2004) aims to determine the optimal distribution of material within the design domain while minimizing the objective function and satisfying the given constraints. Topology optimization can be categorized into two types, continuum and discrete topology optimization, which are determined by the type of the design domain of the system. In a continuum TO, external and internal shapes, as well as inner void areas, are optimized simultaneously. In discrete TO, the procedure determines the optimal connectivity, size, and position of structural members. Deterministic topology optimization (DTO) considers system modeling variables and structural characteristics such as geometry, loading, and material property to be deterministic. Critical reviews of deterministic TO approaches and methods were given by Rozvany (2009) and Sigmund and Maute (2013). Reliability-based topology optimization (RBTO) considers inherent uncertainty, randomness, and variability in the design and manufacturing process by incorporating reliability or safety criteria. The review in this paper focused on SRBTO methods.
Continuum SRBTO
In a continuum topology optimization problem, the continuum domain is discretized by a large number of finite elements that are affected by design variables representing their density. The optimization procedure seeks the optimal placement of material in which the finite elements are determined to be either solid or void within the spatial domain. Structural SRBTO generally is formulated aswhere = vector of material density; and = vector of unities. The material density is obtained by material interpolation or projection schemes such as , where denotes the filtering matrix (Bendsøe and Sigmund 1999). A small lower bound for the filtered density usually is imposed to avoid singularity in solving the finite-element problem.
(11)
Discrete SRBTO
Discrete topology optimization discretizes a design domain into a finite spatial distribution of nodes. All nodes are connected with structural components, such as truss members or beams. For example, an optimal Michell structure can be derived numerically by using a ground structure method (Dorn et al. 1964) composed of a finite number of truss members. This method removes unnecessary members from a highly interconnected ground structure while keeping the initial nodal positions (Ohsaki 2010; Chun et al. 2019a). A general formulation of discrete SRBTO has a mathematical form which is similar to Eq. (11), but has a different type of design variables. Cross-sectional area is a common design variable because the optimal discrete structure is identified by removing bars. In addition, a lower bound of design variables in discrete topology optimization is set to a minimal value introduced to avoid an ill-posed condition such as a singular matrix.
Approaches for SRBDO/TO
A conventional approach to finding solutions in SRBDO/TO involves the nested two-level process: finding the design space by optimization algorithms based on the failure probability of each design, which is computed by structural reliability methods that require iterative calculations at sublevel. Therefore, the system reliability analysis and optimization are primary parts of SRBDO/TO. The reliability analysis forms a loop to identify what is referred to as the most probable failure point (MPP) or design point, using reliability analysis methods (Der Kiureghian 2005) such as the FORM or SORM. This is done by performing constrained nonlinear optimization that finds the shortest distance from the origin in the standard normal space. Subsequently, the system failure probability is computed on the basis of the reliability indexes of limit state functions. A gradient-based optimization algorithm often is employed to find optimal solutions in design optimization problems.
Double-Loop Approach
The double-loop approach is often performed with either the reliability index approach (RIA) (Nikolaidis and Burdisso 1988) or the performance measure approach (PMA) (Tu et al. 1999), because they are equivalent in describing the probabilistic constraint. In RBDO/TO, the RIA approach directly uses the MPP obtained by using FORM, i.e., by solving the optimization problemwhere = outcome of uncorrelated standard normal variables that are transformed from the original random vector ; and = limit state function defined in terms of the standard normal random variables. The reliability index in the standard normal space is obtained as
(12)
(13)
Alternatively, the PMA approach checks the violation of the probabilistic constraint using the minimum value of the limit state function on the surface of the hypersphere with the radius , which is the generalized reliability index corresponding to the target failure probability, i.e., . The performance measure of the limit state function is evaluated by solving the optimization problem
(14)
The double-loop (nested) algorithm is the traditional and direct approach consisting of outer and inner optimization cycles. As the outer optimization algorithm minimizes the objective function, the inner optimization cycle in Eqs. (13) or (14) finds the reliability index or the performance measure to check if the design considered by the outer loop satisfies the probability constraints. The nested iterations are repeated until feasible solutions converge to the prescribed thresholds or the termination criteria are satisfied.
Mogami et al. (2006) formulated the probabilistic constraint as a series system in discrete SRBTO which considered uncertainties in the structural stiffness and eigenfrequency. The upper-bound formula by Ditlevsen (1979b) and FORM are used to compute the reliability index of a series system for the RIA-based SRBTO. The derivatives of the system reliability index with respect to design variables are obtained by the direct differentiation with chain rules. Because only two limit state functions are considered in the framework, the direct differentiation for sensitivity analysis is not computationally expensive. Agarwal and Renaud (2004) employed the second-order response surface approximations (RSAs) of limit state functions governing the failure of system. The samples from a region defined within 3 standard deviations from the MPP obtained at the previous design point were used for the approximation. Based on this system reliability analysis, an approximate subproblem was constructed and solved for reliability constraint evaluation. The use of RSAs within the sublevel optimization of RBDO reduces the computational cost of performing double-loop RBDO. Chun et al. (2019b) developed a method for topology optimization of structures subjected to stochastic excitations. The proposed optimization framework incorporates random processes into the SRBTO framework by the discrete representation method (Der Kiureghian 2000). For linear structures subject to Gaussian processes, the probabilistic constraints on the first-passage probability can be constructed efficiently without performing FORM or SORM. The analytical sensitivity was derived for the first-passage probability constraint using an adjoint method and the parameter sensitivity of the system reliability calculated based on the sequential compounding method (Chun et al. 2015).
Decoupling Approach
To improve the efficiency of SRBDO/TO, various decoupling algorithms have been proposed to eliminate the inner reliability analysis loop. This approach decouples the RBDO procedure, which leads to a sequence of cycles constructed by deterministic optimization followed by the assessment of the reliability of the converged solution in the feasible domain. In general, an equivalent deterministic formulation is used in design optimization. If the system reliability evaluated after DO does not meet the target failure probability, the constraint is pushed in the feasible domain using a shift-vector.
Du and Chen (2004) proposed using the reliability information obtained in the previous cycle to shift the violated deterministic constraints in the feasible domain. Sequential approximate programming was proposed by Cheng et al. (2006). This approach identifies the optimal design solution by solving a sequence of subproblems consisting of the approximate objective and constraint functions by a Taylor series–based linear approximation of the reliability. A recurrence formula based on the optimality conditions for MPPs is applied to find an approximate reliability index and its sensitivity.
Aoues and Chateauneuf (2006) proposed an SRBDO method which formulates SRBDO problems in terms of component constraints and their target reliability indexes. The component reliabilities are pulled down to the level of the target system probability by the least-squares minimization of the gap between the component and the target level. The subupdating procedure ensures that the target system reliability is satisfied by adjusting the target reliabilities of components. Aoues and Chateauneuf further developed a decoupling algorithm to improve computational efficiency by transforming the original double-loop optimization framework, including the nested optimization loop for the subupdating procedure, into an equivalent SRBDO formulation. The finite-difference approximation is used for sensitivity analysis of constraints and the sequential quadratic programming (Schittkowski et al. 1994). The proposed method aimed to find the best compromise between satisfying the target system reliability and optimizing the component performance.
Zou and Mahadevan (2006) developed a simulation-based method to decouple reliability analysis iterations from the nested formulation in RBDO. The system reliability constraint is approximated by a Taylor series expansion and is decoupled from the optimization loop. Reliability and sensitivity analysis, used in the Taylor series expansion, are conducted, and then deterministic optimization is performed using the approximated constraints. To achieve higher accuracy in reliability analysis in the proposed RBDO method, the multimodal adaptive importance sampling approach is used. The MPP of a limit state function is determined by FORM or SORM. A new sampling density function is constructed using the weighted sum of the densities at the representative points. The MPP is used to identify the representative points, which are close to the failure region.
Royset et al. (2001) developed a method for approximately solving RBDO problems for series structural systems. The method reformulates the RBDO problems as deterministic and semi-infinite optimization problems (Terlaky 1998) by replacing the reliability indexes of component events in the series system with a corresponding limit state function within balls in the standard normal space. The radii of balls are determined through iterative schemes with reliability computations. The reformulated deterministic, semi-infinite optimization problem is solved by a robust optimization algorithm, and the system failure probability is assessed by a reliability method. This SRBDO approach was applied to the design of a rectangular column, offshore jacket structure, and a frame structure with multiple failure modes.
Ba-Abbad et al. (2006) decoupled the reliability analysis from the design optimization by replacing a probabilistic constraint with an equivalent deterministic constraint constructed with reliability-based factors of safety. The system reliability is approximated by the first-order upper-bound method (Ditlevsen 1979b), and the target failure probability in SRBDO is considered as a design variable. The MPP is identified approximately as a function of the reliability index obtained by the PMA reliability analysis. Ba-Abbad et al. recommended the use of the truss region optimization algorithm to solve the proposed optimization formulation to ensure the validation of the approximated MPP. Thus, the optimization algorithm solves the approximate deterministic optimization problem and simultaneously finds optimal design variables and the minimum allowable reliability indexes of failure events.
Lee et al. (2008) proposed a decoupling method for RBDO of multidimensional systems using an inverse reliability analysis that employed an MPP-based dimension reduction method (DRM). This method calculates the probability of failure using the constraint shift. The reliability index from the probability calculation then is updated to the new reliability index by a recursive formula to ensure that the probability of failure using the MPP-based DRM is the same as the target failure probability. The MPP then is updated approximately by taking the same radial direction of the current MPP with the change rate of the reliability index from the previous iteration. The updated MPP subsequently is used for the next design iteration in RBDO to obtain the optimum design.
Valdebenito and Schuëller (2011) replaced the nested reliability analysis loop in SRBDO by approximating the failure probability as an explicit function of the design variables. The RBDO subproblem is solved by starting an optimization procedure while constructing a local approximation of the failure probability around a candidate optimal design within the subdomain. A sequence of candidate optimal designs obtained by repeated solving of the RBDO subproblem is expected to converge toward the solution of the original RBDO problem. A line search strategy and weighted approximations of reliability sensitivity analysis are introduced to improve computational efficiency. The finite-difference method is used to compute the parameter sensitivity of the reliability. This method was applied to nonlinear structures subject to dynamic loading, considering the first passage probability.
Single-Loop Approach
In a single-loop approach, the probabilistic constraints are converted into deterministic constraints approximated by exploiting the Karush–Kuhn–Tucker (KKT) optimality conditions. The position vector computed at the MPP can be approximately collinear to the gradient of the performance function when the KKT conditions are satisfied. Optimization is performed in the outer loop with an equivalent constraint along with the KKT conditions. The single-loop approach approximates the MPPs and the target reliability index in relation to the KKT optimality condition. By considering the target failure probability approximated by the procedure described previously as design variables, the necessity of reliability analysis at each iteration can be removed.
Meng et al. (2018) applied the chaos control theory to evaluate approximately the MPPs rather than employing the KKT optimality conditions. This was to address the numerical instability of the single-loop approach that may occur during iterative computations in highly nonlinear problems. Liang et al. (2007) proposed an SRBDO for series systems by transforming a double-loop optimization problem into a single-loop deterministic optimization problem using an approximation of the MPP of each constraint. The KKT condition is imposed to find the approximated MPP rather than solving the nested optimization problem in each iteration. The target failure probabilities of limit state functions are considered as design variables, and the system failure probability is estimated by the bicomponent theoretical bounding formula (Ditlevsen 1979b). The single optimization loop with the approximated MPP improved the efficiency of SRBDO.
Nguyen et al. (2010) integrated the MSR method (Song and Kang 2009; Kang et al. 2012) into a single-loop SRBDO. The MPP of each constraint is approximated by scaling the negative normalized gradient vector with the target reliability index. The failure probability of a system then is estimated by the MSR method efficiently and effectively. By employing the MSR method, applications of the single-loop SRBDO approach were extended to nonseries system events. Furthermore, the MSR method provides a systematic way to compute the sensitivity of the system failure probability with respect to design variables to facilitate the use of gradient-based optimization algorithms in SRBDO. The single-loop approach with the MSR method was extended further and applied to SRBTO. Nguyen et al. (2011) proposed a single-loop SRBTO approach considering statistical dependence between limit state functions of a highly nonlinear problem. The system failure probability and its sensitivity to statistically dependent limit states are computed using the MSR method. To improve the accuracy of the single-loop approach, the following scheme was proposed to address the error by FORM. After approximated MPPs of limit state functions are obtained by employing the KKT conditions in the single-loop approach, the reliability index for each component is evaluated by SORM in each iteration. The radius of the scaling is updated by taking the ratio of the target reliability index to the reliability index obtained by the SORM analysis and multiplying the ratio by the target reliability index in the previous step. As a result, the approximated MPP can be improved based on the updated radius and the normalized gradient vector in each iteration of optimization.
Simulation-Based Approach
Reliability analysis of a system problem defined by multiple failure events often employs simulation techniques such as MCS to avoid difficulty in evaluating multifold integrals in system reliability analysis. The accuracy of MCS is affected significantly by the number of samples and regions describing the system failure event.
The probabilistic sufficient factor approach that combined the concepts of the failure probability and the safety factor was proposed by Qu and Haftka (2004) to improve design response surface approximation for RBDO. After completing the probability calculation of a probabilistic constraint by MCS, the probabilistic sufficiency factor (PSF) is obtained from the target probability and MCS sample size, which is not a computationally expensive process. The proposed method showed that design response surface approximation based on the PSF increases accuracy in regions of a low probability of failure and achieves faster convergence in SRBDO. A simulation-based RBTO of a structure subjected to stochastic excitation was proposed by Bobby et al. (2017). The reliability analysis of the probabilistic constraint in terms of the first-passage probability is computationally expensive in general. In the proposed method, the inverse constraint, which is equivalent to the original probabilistic constraint, is considered along with the damage measure threshold corresponding to the target failure probability. The damage measure threshold is the inverse of a parameter estimated directly from the MC samples of structural damage state. An approximate optimization subproblem then is defined from the simulation-based probabilistic analysis to decouple the probabilistic analysis from the optimization loop. Solutions of the sequence of subproblems in the deterministic form are obtained without performing additional probabilistic analyses, and are expected to meet the original probabilistic constraint associated with the first-passage probability. Papadrakakis and Lagaros (2002) solved RBDO problems using MCS, incorporating the importance sampling technique for reliability analysis. In this method, neural networks (NNs) (Rogers and Mcclelland 2014) are trained and used to reduce computational cost in the evaluation of limit state functions in RBDO. The evolution strategies were used for optimization in conjunction with the NN which was more robust and had more-global behavior than mathematical programming.
Alternatively, an approximate representation of the probability in RBDO with an explicit function of the deterministic variables was studied. Gasser and Schuëller (1997) decoupled the reliability analysis loop from RBDO by applying variance-reducing MCS techniques, in which the limit state function was constructed explicitly by interpolation. Taflanidis and Beck (2009) developed a stochastic subset optimization (SSO) algorithm for reliability optimization problems involving system reliability as the objective function and sensitivity analysis. An augmented problem was formulated with design variables that were considered artificially as uncertain. MCS with samples of the model parameters and the design variables that lead to system failure are performed to obtain information that is used to identify a subset of the design space. The identified design space has the highest likelihood of containing optimal design variables. An adaptive iterative approach using MCMC simulation was applied to reduce the size of subsets until the original design space, including near-optimal design variables, was identified. In addition, SSO was used to perform sensitivity analysis with respect to the uncertain parameters and design variables. The SSO algorithm was extended further to nonparametric stochastic subset optimization (NP-SSO) (Jia and Taflanidis 2013). NP-SSO uses kernel density estimation to approximately evaluate the objective function. Candidate optimal points for the global RBDO minimum then are identified using the approximation of the objective function.
Surrogate-Based Approach
The purpose of employing surrogate models is to replace computationally intensive or expensive assessment of functions due to high nonlinearity and dimensionality with surrogate models which are cheap and easy to evaluate. Various surrogate models (Sudret and Der Kiureghian 2002; Papadrakakis and Lagaros 2002; Bichon et al. 2008) have been used for the reliability analysis in RBDO. Moustapha and Sudret (2019) surveyed surrogate-based RBDO and benchmark studies on computational efficiency and effectiveness.
Li and Wang (2020) proposed a reliability-based multifidelity optimization method that deals with design problems involving low- and high-fidelity data. This method utilizes a Gaussian process modeling approach, in which a limit state function is considered to be a realization of a Gaussian process, to construct a surrogate model by fusing data points with different fidelity levels. The generated surrogate model subsequently was employed to perform reliability and sensitivity analyses in solving RBDO problems.
Dubourg et al. (2011) proposed an adaptive surrogate-based RBDO approach which utilized a refinement technique for reliability estimation. The kriging metamodeling technique is adopted to develop surrogates of the performance functions in which errors in the surrogate models are controlled using the adaptive refinement technique.
Acar et al. (2009) performed SRBDO for automobile structures. To handle computationally expensive simulations without compromising accuracy, the metamodels representing a mathematical relationship between the critical responses of system, design variable, and random variables were constructed using quadratic polynomial response surface, radial basis function, and Gaussian process. The system reliability index and sensitivity analysis of system reliability were computed using MCS with the metamodel. Khatibinia et al. (2013) developed a discrete gravitational search algorithm for SRBDO of RC structures while considering soil–structure interaction effects using a metamodel-based MCS. The metamodel consisting of a weighted least-squares support vector machine and wavelet kernel function was incorporated into RBDO in which system reliability analysis was performed by MCS. The discrete gravitational search algorithm proposed to find the optimum design of structures was enhanced using a passive congregation (He et al. 2004). The global surrogate modeling for RBDO was investigated by Bichon et al. (2011). The efficient global reliability analysis (Bichon et al. 2008) was used to create a Gaussian process model of response functions with a small number of samples. Thus, using the inexpensive surrogate model, the probability of failure can be evaluated with a reduction of computational cost but without significant loss of accuracy. Efficient global optimization (EGO) (Jones et al. 1998), which originally was developed for solving unconstrained optimization problems, was extended to establish a new formulation for enforcing constraints in EGO based on an augmented Lagrangian for RBDO problems. Jensen et al. (2020) proposed a method of reliability-based global design optimization for structures under stochastic excitation. A kriging meta-based surrogate model was employed to assess system failure probability. A stochastic simulation scheme with a transitional Markov-chain Monte Carlo method was utilized to solve an optimization problem.
Heuristic Approach
Heuristic optimization algorithms have been adopted and utilized to obtain optimal solutions of problems that may not have explicit mathematical forms or that may make sensitivity analysis difficult due to implicit or nonsmooth manifold complexity. Greiner and Hajela (2012) proposed an approach of coevolutionary multiobjective formulations for discrete topology optimization considering the randomness of applied loads and material properties. The multiobjective optimization problem was formulated to maximize a system reliability index in terms of design interest while minimizing the deterministic volume of a discrete truss structure. Component reliability indexes of structural elements are evaluated using the first-order second-moment method, and a system reliability analysis with component reliability indexes is computed using the method of Park et al. (2004). A Pareto nondominance criterion was obtained using a coevolution strategy that identifies a complete nondominated solution front with increased search efficiency in the evolutionary algorithm of optimization. Thampan and Krishnamoorthy (2001) developed a modified branch-and-bound (MBB) algorithm to assess the system reliability of discrete structures and used a genetic algorithm (GA) to find an optimal truss structure under uncertainties in loads and strength parameters of the material. The MBB approach imposes bounding conditions of prime member group assignment in the subsequent element failures on the basic bounding technique. The GA based on the fitness evaluation for each candidate solution is implemented to solve RBDO problems of parallel, series, and series of parallel subsystems.
Table 7 compares the aforementioned SRBDO/TO approaches, and flowcharts of their processes are given in Fig. 8. A fair comparison of SRBDO/TO approaches is challenging because of different types of optimization problems; target reliability; and implementations of reliability methods, optimization algorithms, and convergence criteria. However, a few examples of comparisons are available for review in the published literature, such as computational cost comparison between the double- and single-loop approaches by Liang et al. (2014). To solve RBDO problems, the double-loop approach required 1.5–3 times more iterations to find a converged solution than did the single-loop approach. Furthermore, the number of function evaluations in RBDO with the double-loop method was 50–380 times higher than that of the single-loop approach, depending on problem types and the number of design variables. Liang et al. indicated that the efficiency of the single-loop method could be comparable to deterministic optimization. Another such example was provided by Bichon et al. (2013), who performed computation experiments with double-loop, decoupling, and surrogate-based approaches for a short-column RBDO problem. The results showed that the surrogate-based method in RBDO could require less than half the number of function evaluations needed for the decoupling method. The decoupling method for the same problem required one-third fewer function evaluations than the double-loop method. The decoupling-based RBDO generally is more efficient than the double-loop formulation, but more computationally expensive than the single-loop formulation. Furthermore, the computational efficiency of a surrogate-based approach in RBDO and of others was illustrated using numerical examples by Moustapha and Sudret (2019).
| Approach | Efficiency of implementation and computation | Feasibility/accuracy of solutions | Other remarks |
|---|---|---|---|
| Double-loop (Chun et al. 2019a, Mogami et al. 2006; Agarwal and Renaud 2004) | Can be extremely inefficient when there are many probabilistic constraints or high dimensional system reliability analysis is needed. | It has high feasibility/accuracy because the algorithm assesses the reliability in each iteration given design solutions during the optimization process. | There is flexibility in the choice of optimization algorithm and reliability method. |
| Decoupling (Du and Chen 2004; Cheng et al. 2006; Aoues and Chateauneuf 2006; Zou and Mahadevan 2006; Royset et al. 2001; Ba-Abbad et al. 2006; Lee et al. 2008; Valdebenito and Schuëller 2011) | If reliability analysis dominates the overall computational cost, this approach may still be inefficient for practical RBDO applications because in general the approach still searches for the MPPs in the reliability assessment loop. | Accuracy of solutions can be dependent on the approximate representation of the probability. High-order approximation to the limit state function can result in more accurate solutions than single-loop results. | |
| Single-loop (Liang et al. 2007; Nguyen et al. 2010, 2011) | Computationally more affordable than double-loop strategies, and computational efficiency is improved by eliminating the inner reliability loops. | Accuracy/feasibility of final solutions can be improved by employing a more accurate reliability method such as SORM. | Some single-loop approaches require the second-order derivatives which increase the computational cost. |
| Simulation (Qu and Haftka 2004; Bobby and Kareem 2017; Papadrakakis and Lagaros 2002; Gasser and Schuëller 1997; Taflanidis and Beck 2009; Jia and Taflanidis 2013) | It is relatively easy to implement simulation techniques in optimization. It shows efficiency for the assessment of a high-dimensional system reliability problem. However, it will suffer from heavy computational burden for sensitivity analysis with respect to a large number of design variables. | Sample sizes for simulations affect the overall accuracy of reliability assessment and sensitivity as well as the feasibility of converged solutions. | — |
| Surrogate model (Dubourg et al. 2011; Acar et al. 2009; Khatibinia et al. 2013; Bichon et al. 2011; Jones et al. 1998) | Effort required for numerical evaluations of functions is generally minimal once a surrogate model achieving a prescribed accuracy is constructed. | Accuracy/feasibility can be guaranteed by using sufficient samples and simulations and creating models showing accuracy in areas where reliability is needed. | Training surrogate model can be challenging when the vector of inputs is defined in a high-dimensional space. |
| Heuristic (Greiner and Hajela 2012; Thampan and Krishnamoorthy 2001) | This approach may be used to find an acceptable solution to optimization problems with incomplete information and limited data. Implementation of the heuristic approach is relatively easy because it does not make use of gradients. This approach is ideally suited for parallel computing settings to improve computational efficiency. | Optimal solutions can be dependent on the set of generated individuals. Thus, search process with a large feasible set of generations will lead to a good design solution. | Less prone to converging to local optima. |
Concluding Remarks
The first part of this review paper summarized SSR methods developed for Boolean system events. For both time-invariant and variant problems, various analytical, approximate, and simulation-based methods in the literature were summarized. An SSR method needs to be selected carefully based on the accuracy, efficiency, and implementation issues summarized in Tables 1–5. For time-invariant methods, analytical SSR methods need to be developed further to reduce the accumulation of estimation errors and analysis time, especially for systems with large numbers of components; to handle parameters following nonnormal distributions more effectively; and to facilitate implementations. Simulation-based methods need further development to reduce the computational cost, especially for highly reliable systems; to improve accuracy; and to mitigate the curse of dimensionality issues. On the other hand, time variant-methods require solid establishment of component-level time-variant analysis methods that can resolve the issues of high dimensionality and nonlinearity, and of related time-invariant system reliability analysis methods. A common challenge is to reduce the computational cost without significantly compromising the estimation accuracy. This is important, especially when complex and detailed numerical simulations should be performed or when the reliability analysis is included in an iterative framework of optimization or inverse analysis, which requires multiple function calls. The strategies to overcome the limitations may include further theoretical developments, effective use of machine learning–based surrogates, and the use of advanced computing power including parallel high-performance computing.
The next section of this paper reviewed SSR methods that can consider sequential failures in structural systems. Table 6 compares the reviewed SSR approaches. When sequential failures are considered, the failure domain may consist of multiple regions and/or may exhibit high nonlinearity, which makes the problem more challenging. Various methods in the literature were categorized into numerical approaches, response surface–based approaches, and failure path approaches. The numerical approaches were categorized further into two subgroups: analytical formulation–based methods, and MCS-based methods. In addition, the failure path approaches were categorized further into deterministic search, probabilistic local search, and probabilistic global search. Direct comparison of these methods is challenging and may not be reasonable, because target SSR problems can differ in terms of structural types, level of structural complexity, failure modes and definitions, and statistical modeling of random variables. More attention should be paid to the ongoing improvement of these methods, which is related closely to the further development of SSR methods for Boolean system events and innovative integration of reliability analysis with machine learning theories and adaptive surrogate models to address computational challenges caused by the complexity of the problem.
In SRBDO/TO (Table 7 and Fig. 8), as demands for addressing practical questions and needs increase, new challenges and opportunities also arise. First, a large-scale multiobjective SRBDO/TO remains challenging even though the advancement of computing power and technologies makes it faster to solve large complex problems. Thus, efficient and effective SSR methods and SRBDO/TO frameworks integrated with versatile optimization algorithms are indispensable. Furthermore, a systematic framework for interactive multiobjective decision-making using Pareto optimal solutions is needed to reduce the gap between research developments and actual decision-making practices. Second, nonconvexity of objective and constraint functions in SRBDO/TO makes optimization problems difficult. Third, nonstatic optimization cases such as transient problems dealing with time-dependent responses of systems or multistate questions considering intermediate states of structural failure may add an extra layer of complexity. Fourth, to compute sensitivity for large-scale SRBDO/TO problems, gradient-based optimization algorithms can be expensive or infeasible. Because SSR analysis and optimization are essential and crucial parts of SRBDO/TO, the development and continuous improvement of each field and their novel integration are expected to advance the technology and promote applications in engineering practice.
Data Availability Statement
No data, models, or code were generated or used during the study.
Acknowledgments
The corresponding author is supported by the Institute of Construction and Environmental Engineering at Seoul National University. The fourth author is supported by the Office of Research at Syracuse University.
References
Acar, E., K. Solanki, E. Acar, and K. Solanki. 2009. “System reliability based vehicle design for crashworthiness and effects of various uncertainty reduction measures.” Struct. Multidiscip. Optim. 39 (3): 311–325. https://doi.org/10.1007/s00158-008-0327-3.
Adduri, P. R., and R. C. Penmetsa. 2009. “System reliability analysis for mixed uncertain variables.” Struct. Saf. 31 (5): 375–382. https://doi.org/10.1016/j.strusafe.2009.02.001.
Agarwal, H., and J. E. Renaud. 2004. “Reliability based design optimization using response surfaces in application to multidisciplinary systems.” Eng. Optim. 36 (3): 291–311. https://doi.org/10.1080/03052150410001666578.
Ambartzumian, R., A. Der Kiureghian, V. Ohaniana, and H. Sukiasiana. 1998. “Multinormal probability by sequential conditioned importance sampling: Theory and application.” Probab. Eng. Mech. 13 (4): 299–308. https://doi.org/10.1016/S0266-8920(98)00003-4.
Aoues, Y., and A. Chateauneuf. 2006. “Reliability-based optimization of structural systems by adaptive target safety—Application to RC frames.” Struct. Saf. 30 (2): 144–161. https://doi.org/10.1016/j.strusafe.2006.10.002.
Au, S. K., and J. L. Beck. 2001. “Estimation of small failure probabilities in high dimensions by subset simulation.” Probab. Eng. Mech. 16 (4): 263–277. https://doi.org/10.1016/S0266-8920(01)00019-4.
Ayyub, B. M., U. O. Akpan, T. S. Koko, and T. Dunbar. 2015. “Reliability-based optimal design of steel box structures. I: Theory.” ASCE-ASME J. Risk Uncertainty Eng. Syst. Part A: Civ. Eng. 1 (3): 04015009. https://doi.org/10.1061/AJRUA6.0000829.
Ba-Abbad, M. A., E. Nikolaidis, and R. K. Kapania. 2006. “New approach for system reliability-based design optimization.” AIAA J. 44 (5): 1087–1096. https://doi.org/10.2514/1.17237.
Bendsøe, M. P., and O. Sigmund. 1999. “Material interpolation schemes in topology optimization.” Arch. Appl. Mech. 69 (9–10): 635–654. https://doi.org/10.1007%2Fs004190050248.
Bendsøe, M. P., and O. Sigmund. 2004. Topology optimization. Berlin: Springer.
Bichon, B. J., M. S. Eldred, S. Mahadevan, and J. M. McFarland. 2013. “Efficient global surrogate modeling for reliability-based design optimization.” J. Mech. Des. 135 (1): 011009. https://doi.org/10.1115/1.4022999.
Bichon, B. J., M. S. Eldred, L. P. Swiler, S. Mahadevan, and J. M. McFarland. 2008. “Efficient global reliability analysis for nonlinear implicit performance functions.” AIAA J. 46 (10): 2459–2468. https://doi.org/10.2514/1.34321.
Bichon, B. J., J. M. McFarland, and S. Mahadevan. 2011. “Efficient surrogate models for reliability analysis of systems with multiple failure modes.” Reliab. Eng. Syst. Saf. 96 (10): 1386–1395. https://doi.org/10.1016/j.ress.2011.05.008.
Bjerager, P. 1989. “Plastic systems reliability by LP and FORM.” Comput. Struct. 31 (2): 187–196. https://doi.org/10.1016/0045-7949(89)90224-1.
Bobby, S., A. Suksuwan, S. M. J. Spence, and A. Kareem. 2017. “Reliability-based topology optimization of uncertain building systems subject to stochastic excitation.” Struct. Saf. 66 (May): 1–16. https://doi.org/10.1016/j.strusafe.2017.01.005.
Bonferroni, C. 1936. Vol. 8 of Teoria statistica delle classi e calcolo delle probabilita, 3–62. Florence, Italy: Pubblicazioni del R Istituto Superiore di Scienze Economiche e Commerciali di Firenze.
Boole, G. 1911. The laws of thought (1854). London: Open Court.
Bourinet, J. M., F. Deheeger, and M. Lemaire. 2011. “Assessing small failure probabilities by combined subset simulation and support vector machines.” Struct. Saf. 33 (6): 343–353. https://doi.org/10.1016/j.strusafe.2011.06.001.
Box, G. E., W. G. Hunter, and J. S. Hunter. 1978. Statistics for experimenters. New York: Wiley.
Byers, W. G., M. J. Marley, J. Mohammadi, R. J. Nielsen, and S. Sarkani. 1997. “Fatigue reliability reassessment applications: State-of-the-art paper.” J. Struct. Eng. 123 (3): 277–285. https://doi.org/10.1061/(ASCE)0733-9445(1997)123:3(277).
Byun, J.-E., H.-M. Noh, and J. Song. 2017. “Reliability growth analysis of k-out-of-N systems using matrix-based system reliability method.” Reliab. Eng. Syst. Saf. 165 (Sep): 410–421. https://doi.org/10.1016/j.ress.2017.05.001.
Byun, J.-E., and J. Song. 2017. “Structural system reliability, reloaded.” Chap. 2-2 in Risk and reliability analysis: Theory and applications, edited by P. Gardoni. Berlin: Springer.
Byun, J.-E., and J. Song. 2020. “Bounds on reliability of larger systems by linear programming with delayed column generation.” J. Eng. Mech. 146 (4): 04020008. https://doi.org/10.1061/(ASCE)EM.1943-7889.0001717.
Byun, J.-E., K. Zwirglmaier, D. Straub, and J. Song. 2019. “Matrix-based Bayesian network for efficient memory storage and flexible inference.” Reliab. Eng. Syst. Saf. 185 (May): 533–545. https://doi.org/10.1016/j.ress.2019.01.007.
Carbonari, R. C., E. C. N. Silva, and G. H. Paulino. 2007. “Topology optimization design of functionally graded bimorph-type piezoelectric actuators.” Smart Mater. Struct. 16 (6): 2605–2620. https://doi.org/10.1088/0964-1726/16/6/065.
Cheng, G., L. Xu, and L. Jiang. 2006. “A sequential approximate programming strategy for reliability-based structural optimization.” Comput. Struct. 84 (21): 1353–1367. https://doi.org/10.1016/j.compstruc.2006.03.006.
Cheng, J., W. Lu, W. Hu, Z. Liu, Y. Zhang, and J. Tan. 2019. “Hybrid reliability-based design optimization of complex structures with random and interval uncertainties based on ASS-HRA.” IEEE Access 7: 87097–87109. https://doi.org/10.1109/ACCESS.2019.2926145.
Chun, J. 2016. “Reliability−based topology optimization frameworks for the design of structures subjected to random excitations.” Ph.D. dissertation, Dept. of Civil and Environmental Engineering, Univ. of Illinois, Urbana-Champaign.
Chun, J., G. H. Paulino, and J. Song. 2019a. “Reliability-based topology optimization by ground structure method employing a discrete filtering technique.” Struct. Multidiscip. Optim. 60 (3): 1035–1058. https://doi.org/10.1007/s00158-019-02255-1.
Chun, J., J. Song, and G. H. Paulino. 2015. “Parameter sensitivity of system reliability using sequential compounding method.” Struct. Saf. 55 (Jul): 26–36. https://doi.org/10.1016/j.strusafe.2015.02.001.
Chun, J., J. Song, and G. H. Paulino. 2019b. “System-reliability-based design and topology optimization of structures under constraints on first-passage probability.” Struct. Saf. 76 (Jan): 81–94. https://doi.org/10.1016/j.strusafe.2018.06.006.
Coccon, M. N., J. Song, S.-Y. Ok, and U. Galvanetto. 2017. “A new approach to system reliability analysis of offshore structures using dominant failure modes identified by selective searching technique.” KSCE J. Civ. Eng. 21 (6): 2360–2372. https://doi.org/10.1007/s12205-016-1192-z.
Daniels, H. E. 1945. “The statistical theory of the strength of bundles of threads.” Proc. R. Soc. London, Ser. A 183 (995): 405–435. https://doi.org/10.1098/rspa.1945.0011.
Der Kiureghian, A. 2000. “Geometry of random vibrations and solutions by FORM and SORM.” Probab. Eng. Mech. 15 (1): 81–90. https://doi.org/10.1016/S0266-8920(99)00011-9.
Der Kiureghian, A. 2005. “First- and second-order reliability methods.” Chap. 14 in Engineering design reliability handbook, edited by E. Nikolaidis, D. Ghiocel, and S. Singhal. Boca Raton, FL: CRC Press.
Der Kiureghian, A. 2006. “System reliability revisited.” In Proc., 3rd ASRANet Int. Colloquium. Glasgow, Scotland: ASRANet.
Der Kiureghian, A., O. D. Ditlevsen, and J. Song. 2007. “Availability, reliability and downtime of systems with repairable components.” Reliab. Eng. Syst. Saf. 92 (2): 231–242. https://doi.org/10.1016/j.ress.2005.12.003.
Der Kiureghian, A., and J. Song. 2008. “Multi-scale reliability analysis and updating of complex systems by use of linear programming.” Reliab. Eng. Syst. Saf. 93 (2): 288–297. https://doi.org/10.1016/j.ress.2006.10.022.
Dey, A., and S. Mahadevan. 1998. “Ductile structural system reliability analysis using adaptive importance sampling.” Struct. Saf. 20 (2): 137–154. https://doi.org/10.1016/S0167-4730(97)00033-7.
Ditlevsen, O. 1979a. “Generalized second moment reliability index.” J. Struct. Mech. 7 (4): 435–451. https://doi.org/10.1080/03601217908905328.
Ditlevsen, O. 1979b. “Narrow reliability bounds for structural systems.” J. Struct. Mech. 7 (4): 453–472. https://doi.org/10.1080/03601217908905329.
Ditlevsen, O., and P. Bjerager. 1984. “Reliability of highly redundant plastic structures.” J. Eng. Mech. 110 (5): 671–693. https://doi.org/10.1061/(ASCE)0733-9399(1984)110:5(671).
Dorn, W. S., R. E. Gomory, and H. J. Greenberg. 1964. “Automatic design of optimal structures.” J. Mécanique 3 (1): 25–52.
Draper, N. R., and H. Smith. 1998. Applied regression analysis. New York: Wiley.
Du, W., Y. Luo, and Y. Wang. 2019. “Time-variant reliability analysis using the parallel subset simulation.” Reliab. Eng. Syst. Saf. 182 (Feb): 250–257. https://doi.org/10.1016/j.ress.2018.10.016.
Du, X., and W. Chen. 2004. “Sequential optimization and reliability assessment method for efficient probabilistic design.” J. Mech. Des. 126 (2): 225–233. https://doi.org/10.1115/1.1649968.
Dubourg, V., D. Sudret, and J.-M. Bourinet. 2011. “Reliability-based design optimization using kriging surrogates and subset simulation.” Struct. Multidiscip. Optim. 44 (5): 673–690. https://doi.org/10.1007/s00158-011-0653-8.
Dunnett, C. W., and M. Sobel. 1955. “Approximations to the probability integral and certain percentage points of a multivariate analogue of Student’s -distribution.” Biometrika 42 (1–2): 258–267. https://doi.org/10.1093/biomet/42.1-2.258.
Echard, B., N. Gayton, and M. Lemaire. 2011. “AK-MCS: An active learning reliability method combining Kriging and Monte Carlo Simulation.” Struct. Saf. 33 (2): 145–154. https://doi.org/10.1016/j.strusafe.2011.01.002.
Enevoldsen, I., and J. D. Sørensen. 1994. “Reliability-based optimization in structural engineering.” Struct. Saf. 15 (3): 169–196. https://doi.org/10.1016/0167-4730(94)90039-6.
Enright, M. P. 2000. “Time-variant reliability of reinforced concrete bridges under environmental attack.” Ph.D. thesis, Dept. of Civil, Environmental, and Architectural Engineering, Univ. of Colorado.
Enright, M. P., and D. M. Frangopol. 1998. “Failure time prediction of deteriorating fail-safe structures.” J. Struct. Eng. 124 (12): 1448–1457. https://doi.org/10.1061/(ASCE)0733-9445(1998)124:12(1448).
Enright, M. P., and D. M. Frangopol. 1999. “Reliability-based condition assessment of deteriorating concrete bridges considering load redistribution.” Struct. Saf. 21 (2): 159–195. https://doi.org/10.1016/S0167-4730(99)00015-6.
Fauriat, W., and N. Gayton. 2014. “AK-SYS: An adaptation of the AK-MCS method for system reliability.” Reliab. Eng. Syst. Saf. 123 (Mar): 137–144. https://doi.org/10.1016/j.ress.2013.10.010.
Frangopol, D. M., R. B. Corotis, and R. Rackwitz. 1997. “Reliability and optimization of structural systems.” In Proc., 7th IFIP WG7.5 Working Conf. on Reliability and Optimization of Structural Systems. Pergamon, Turkey: Pergamon Press.
Frangopol, D. M., and K. Maute. 2004. “Reliability-based optimization of civil and aerospace structural systems.” Chap. 24 in Engineering design reliability handbook, edited by E. Nikolaidis, D. Ghiocel, and S. Singhal. Boca Raton, FL: CRC Press.
Fussell, J. B. 1975. “How to hand-calculate system reliability and safety characteristics.” IEEE Trans. Reliab. R-24 (3): 169–174. https://doi.org/10.1109/TR.1975.5215142.
Gasser, M., and G. I. Schuëller. 1997. “Reliability-based optimization of structural systems.” Math. Methods Oper. Res. 46 (3): 287–307. https://doi.org/10.1007/BF01194858.
Genz, A. 1992. “Numerical computation of multivariate normal probabilities.” J. Comput. Graphical Stat. 1 (2): 141–149. https://doi.org/10.1080/10618600.1992.10477010.
Genz, A. 2018. “Alan Genz website.” Accessed January 1, 2021. http://www.math.wsu.edu/faculty/genz/homepage.
Gharaibeh, E. S., D. M. Frangopol, and T. Onoufriou. 2002. “Reliability-based importance assessment of structural members with applications to complex structures.” Comput. Struct. 80 (12): 1113–1131. https://doi.org/10.1016/S0045-7949(02)00070-6.
Ghosn, M., F. Moses, and D. M. Frangopol. 2010. “Redundancy and robustness of highway bridge superstructures and substructures.” Struct. Infrastruct. Eng. 6 (1–2): 257–278. https://doi.org/10.1080/15732470802664498.
Gollwitzer, S., and R. Rackwitz. 1983. “Equivalent components in first-order system reliability.” Reliab. Eng. 5 (2): 99–115. https://doi.org/10.1016/0143-8174(83)90024-0.
Greiner, D., and P. Hajela. 2012. “Truss topology optimization for mass and reliability considerations—Co-evolutionary multiobjective formulations.” Struct. Multidiscip. Optim. 45 (4): 589–613. https://doi.org/10.1007/s00158-011-0709-9.
Guenard, Y. F. 1984. Application of system reliability analysis to offshore structures. Stanford, CA: John A. Blume Earthquake Engineering Center.
Gupta, S., P. van Gelder, and M. Pandey. 2006. “Time-variant reliability analysis for series systems with log-normal vector response.” In Proc., Advances in Engineering Structures, Mechanics and Construction, 747–759. Dordrecht, Netherlands: Springer.
Haftka, R. T., and Z. Gu¨rdal. 1992. Elements of structural optimization. Dordrecht, Netherlands: Springer.
Hashemolhosseini, S. 2013. “Algorithmic component and system reliability analysis of truss structures.” Ph.D. dissertation, Dept. of Civil Engineering, Stellenbosch Univ.
He, S., Q. H. Wu, J. Y. Wen, J. R. Saunders, and R. C. Paton. 2004. “A particle swarm optimizer with passive congregation.” BioSystems 78 (1–3): 135–147. https://doi.org/10.1016/j.biosystems.2004.08.003.
Hendawi, S., and D. M. Frangopol. 1994. “System reliability and redundancy in structural design and evaluation.” Struct. Saf. 16 (1–2): 47–71. https://doi.org/10.1016/0167-4730(94)00027-N.
Hohenbichler, M., and R. Rackwitz. 1982. “First-order concepts in system reliability.” Struct. Saf. 1 (3): 177–188. https://doi.org/10.1016/0167-4730(82)90024-8.
Hu, Z., S. Nannapaneni, and S. Mahadevan. 2017. “Efficient Kriging surrogate modeling approach for system reliability analysis.” Artif. Intell. Eng. Des. Anal. Manuf. 31 (2): 143–160. https://doi.org/10.1017/S089006041700004X.
Huang, X., and Y. M. Xie. 2008. “Topology optimization of nonlinear structures under displacement loading.” Eng. Struct. 30 (7): 2057–2068. https://doi.org/10.1016/j.engstruct.2008.01.009.
Hunter, D. 1976. “An upper bound for the probability of a union.” J. Appl. Probab. 13 (3): 597–603. https://doi.org/10.2307/3212481.
Jensen, H. A., D. J. Jerez, and M. Valdebenito. 2020. “An adaptive scheme for reliability-based global design optimization: A Markov chain Monte Carlo approach.” Mech. Syst. Sig. Process. 143 (Sep): 106836. https://doi.org/10.1016/j.ymssp.2020.106836.
Jia, G., and A. A. Taflanidis. 2013. “Non-parametric stochastic subset optimization for optimal-reliability design problems.” Comput. Struct. 126 (Sep): 86–99. https://doi.org/10.1016/j.compstruc.2012.12.009.
Jiang, S.-H., J. Huang, and C.-B. Zhou. 2017. “Efficient system reliability analysis of rock slopes based on Subset simulation.” Comput. Geotech. 82 (Feb): 31–42. https://doi.org/10.1016/j.compgeo.2016.09.009.
Jones, D. R., M. Schonlau, and W. J. Welch. 1998. “Efficient global optimization of expensive black-box functions.” J. Global Optim. 13 (4): 455–492. https://doi.org/10.1023/A:1008306431147.
Kang, W.-H., Y.-J. Lee, J. Song, and B. Gencturk. 2012. “Further development of matrix-based system reliability method and applications to structural systems.” Struct. Infrastruct. Eng. 8 (5): 441–457. https://doi.org/10.1080/15732479.2010.539060.
Kang, W.-H., and J. Song. 2010. “Evaluation of multivariate normal integrals for general systems by sequential compounding.” Struct. Saf. 32 (1): 35–41. https://doi.org/10.1016/j.strusafe.2009.06.001.
Kang, W.-H., J. Song, and P. Gardoni. 2008. “Matrix-based system reliability method and applications to bridge networks.” Reliab. Eng. Syst. Saf. 93 (11): 1584–1593. https://doi.org/10.1016/j.ress.2008.02.011.
Kang, Z., and Y. Luo. 2009. “Non-probabilistic reliability-based topology optimization of geometrically nonlinear structures using convex models.” Comput. Methods Appl. Mech. Eng. 198 (41–44): 3228–3238. https://doi.org/10.1016/j.cma.2009.06.001.
Kanjilal, O., and C. S. Manohar. 2015. “Markov chain splitting methods in structural reliability integral estimation.” Probab. Eng. Mech. 40 (Apr): 42–51. https://doi.org/10.1016/j.probengmech.2015.02.004.
Karamchandani, A., J. I. Dalane, and P. Bjerager. 1992. “Systems reliability approach to fatigue of structures.” J. Struct. Eng. 118 (3): 684–700. https://doi.org/10.1061/(ASCE)0733-9445(1992)118:3(684).
Khatibinia, M., E. Salajegheh, J. Salajegheh, and M. J. Fadaee. 2013. “Reliability-based design optimization of reinforced concrete structures including soil-structure interaction using a discrete gravitational search algorithm and a proposed metamodel.” Eng. Optim. 45 (10): 1147–1165. https://doi.org/10.1080/0305215X.2012.725051.
Kim, D.-S., S.-Y. Ok, J. Song, and H.-M. Koh. 2013. “System reliability analysis using dominant failure modes identified by selective searching technique.” Reliab. Eng. Syst. Saf. 119 (Nov): 316–331. https://doi.org/10.1016/j.ress.2013.02.007.
Kounias, E. G. 1968. “Bounds for the probability of a union, with applications.” Ann. Math. Stat. 39 (6): 2154–2158. https://doi.org/10.1214/aoms/1177698049.
Krog, L., A. Tucker, A. Uk, M. Kemp, and R. Boyd. 2004. “Topology optimization of aircraft wing box ribs.” In Proc., AIAA Multidisciplonary Analysis and Optimization Conf. Reston, VA: American Institute of Aeronautics and Astronautics. https://doi.org/10.2514/6.2004-4481.
Kurtz, N., and J. Song. 2013. “Cross-entropy-based adaptive importance sampling using Gaussian mixture.” Struct. Saf. 42 (May): 35–44. https://doi.org/10.1016/j.strusafe.2013.01.006.
Lee, I., K. K. Choi, L. Du, and D. Gorsich. 2008. “Inverse analysis method using MPP-based dimension reduction for reliability-based design optimization of nonlinear and multi-dimensional systems.” Comput. Methods Appl. Mech. Eng. 198 (1): 14–27. https://doi.org/10.1016/j.cma.2008.03.004.
Lee, Y.-J., and J. Song. 2011. “Risk analysis of fatigue-induced sequential failures by branch-and-bound method employing system reliability bounds.” J. Eng. Mech. 137 (12): 807–821. https://doi.org/10.1061/(ASCE)EM.1943-7889.0000286.
Lee, Y.-J., and J. Song. 2012. “Finite-element-based system reliability analysis of fatigue-induced sequential failures.” Reliab. Eng. Syst. Saf. 108 (Dec): 131–141. https://doi.org/10.1016/j.ress.2012.05.007.
Li, M., and Z. Wang. 2020. “Reliability-based multifidelity optimization using adaptive hybrid learning.” ASCE-ASME J. Risk Uncertainty Eng. Syst., Part B: Mech. Eng. 6 (2): 021005. https://doi.org/10.1115/1.4044773.
Liang, J., Z. P. Mourelatos, and E. Nikolaidis. 2007. “A single-loop approach for system reliability-based design optimization.” J. Mech. Des. 129 (12): 1215–1222. https://doi.org/10.1115/1.2779884.
Liang, J., Z. P. Mourelatos, and J. Tu. 2014. “A single-loop method for reliability-based design optimization.” In Proc., 30th Design Automation Conf., 419–430. New York: ASME.
Liu, Y. W., and F. Moses. 1994. “A sequential response surface method and its application in the reliability analysis of aircraft structural systems.” Struct. Saf. 16 (1–2): 39–46.
Lu, N., Y. Liu, and M. Beer. 2018. “System reliability evaluation of in-service cable-stayed bridges subjected to cable degradation.” Struct. Infrastruct. Eng. 14 (11): 1486–1498. https://doi.org/10.1080/15732479.2018.1459743.
Mahadevan, S., and P. Raghothamachar. 2000. “Adaptive simulation for system reliability analysis of large structures.” Comput. Struct. 77 (6): 725–734. https://doi.org/10.1016/S0045-7949(00)00013-4.
Mahadevan, S., and Q. Xiao. 1995. “Time-variant reliability of brittle structural systems.” J. Eng. Mech. 121 (3): 414–423. https://doi.org/10.1061/(ASCE)0733-9399(1995)121:3(414).
Melchers, R. E., and A. T. Beck. 2018. Structural reliability analysis and prediction. New York: Wiley.
Melchers, R. E., and L. K. Tang. 1984. “Dominant failure modes in stochastic structural systems.” Struct. Saf. 2 (2): 127–143. https://doi.org/10.1016/0167-4730(84)90016-X.
Meng, Z., D. Yang, H. Zhou, and B. P. Wang. 2018. “Convergence control of single loop approach for reliability-based design optimization.” Struct. Multidiscip. Optim. 57 (3): 1079–1091. https://doi.org/10.1007/s00158-017-1796-z.
Mettas, A., and M. Savva. 2001. “System reliability analysis: The advantages of using analytical methods to analyze non-repairable systems.” In Proc., Int. Symp. on Product Quality and Integrity (Cat. No. 01CH37179), 80–85. New York: IEEE.
Mogami, K., S. Nishiwaki, K. Izui, M. Yoshimura, and N. Kogiso. 2006. “Reliability-based structural optimization of frame structures for multiple failure criteria using topology optimization techniques.” Struct. Multidiscip. Optim. 32 (4): 299–311. https://doi.org/10.1007/s00158-006-0039-5.
Mori, Y., and B. R. Ellingwood. 1993a. Methodology for reliability based condition assessment: Application to concrete structures in nuclear plants. Washington, DC: Nuclear Regulatory Commission.
Mori, Y., and B. R. Ellingwood. 1993b. “Reliability-based service-life assessment of aging concrete structures.” J. Struct. Eng. 119 (5): 1600–1621. https://doi.org/10.1061/(ASCE)0733-9445(1993)119:5(1600).
Mori, Y., and T. Kato. 2003. “Multinormal integrals by importance sampling for series system reliability.” Struct. Saf. 25 (4): 363–378. https://doi.org/10.1016/S0167-4730(03)00015-8.
Moses, F. 1977. “Structural system reliability and optimization.” Comput. Struct. 7 (2): 283–290. https://doi.org/10.1016/0045-7949(77)90047-5.
Moses, F. 1982. “System reliability developments in structural engineering.” Struct. Saf. 1 (1): 3–13. https://doi.org/10.1016/0167-4730(82)90011-X.
Moustapha, M., and B. Sudret. 2019. “Surrogate-assisted reliability-based design optimization: A survey and a unified modular framework.” Struct. Multidiscip. Optim. 60 (5): 2157–2176. https://doi.org/10.1007/s00158-019-02290-y.
Murotsu, Y. 1984. “Automatic generation of stochastically dominant modes of structural failure in frame structures.” Struct. Saf. 2 (1): 17–25. https://doi.org/10.1016/0167-4730(84)90004-3.
Murotsu, Y., H. Okada, M. Yonezawa, G. Martin, and K. Taguchi. 1982. “Automatic generation of stochastically dominant modes of structural failure in frame structure.” Bull. Univ. Osaka Prefecture Ser. A. Eng. Nat. Sci. 30 (2): 85–101.
Neves, M. M., H. Rodrigues, and J. M. Guedes. 1995. “Generalized topology design of structures with a buckling load criterion.” Struct. Optim. 10 (2): 71–78. https://doi.org/10.1007/BF01743533.
Nguyen, T. H., J. Song, and G. H. Paulino. 2010. “Single-loop system reliability-based design optimization using matrix-based system reliability method: Theory and applications.” J. Mech. Des. 132 (1): 11005. https://doi.org/10.1115/1.4000483.
Nguyen, T. H., J. Song, and G. H. Paulino. 2011. “Single-loop system reliability-based topology optimization considering statistical dependence between limit-states.” Struct. Multidiscip. Optim. 44 (5): 593–611. https://doi.org/10.1007/s00158-011-0669-0.
Nikolaidis, E., and R. Burdisso. 1988. “Reliability based optimization: A safety index approach.” Comput. Struct. 28 (6): 781–788. https://doi.org/10.1016/0045-7949(88)90418-X.
Ohsaki, M. 2010. Optimization of finite dimensional structures. Boca Raton, FL: CRC Press.
Palmer, J. A., R. Mejia-Alvarez, J. L. Best, and K. T. Christensen. 2012. “Particle-image velocimetry measurements of flow over interacting barchan dunes.” Exp. Fluids 52 (3): 809–829. https://doi.org/10.1007/s00348-011-1104-4.
Pandey, M. D. 1998. “An effective approximation to evaluate multinormal integrals.” Struct. Saf. 20 (1): 51–67. https://doi.org/10.1016/S0167-4730(97)00023-4.
Papadrakakis, M., and N. D. Lagaros. 2002. “Reliability-based structural optimization using neural networks and Monte Carlo simulation.” Comput. Methods Appl. Mech. Eng. 191 (32): 3491–3507. https://doi.org/10.1016/S0045-7825(02)00287-6.
Park, S., S. Choi, C. Sikorsky, and N. Stubbs. 2004. “Efficient method for calculation of system reliability of a complex structure.” Int. J. Solids Struct. 41 (18–19): 5035–5050. https://doi.org/10.1016/j.ijsolstr.2004.04.028.
Patelli, E., H. J. Pradlwarter, and G. I. Schuëller. 2011. “On multinormal integrals by importance sampling for parallel system reliability.” Struct. Saf. 33 (1): 1–7. https://doi.org/10.1016/j.strusafe.2010.04.002.
Paulino, G. H., and E. C. N. Silva. 2005. “Design of functionally graded structures using topology optimization.” In Vol. 492 of Proc., Materials Science Forum, 435–440. Bäch, Switzerland: Trans Tech Publications.
Peressini, A. L., F. E. Sullivan, and J. J. Uhl. 1988. The mathematics of nonlinear programming. New York: Springer.
Pradlwarter, H. J., G. I. Schueller, P. S. Koutsourelakis, and D. C. Charmpis. 2007. “Application of line sampling simulation method to reliability benchmark problems.” Struct. Saf. 29 (3): 208–221. https://doi.org/10.1016/j.strusafe.2006.07.009.
Qu, X., and R. T. Haftka. 2004. “Reliability-based design optimization using probabilistic sufficiency factor.” Struct. Multidiscip. Optim. 27 (5): 314–325.
Rice, S. O. 1944. “Mathematical analysis of random noise.” Bell Syst. Tech. J. 23 (3): 282–332. https://doi.org/10.1002/j.1538-7305.1944.tb00874.x.
Rice, S. O. 1945. “Mathematical analysis of random noise.” Bell Syst. Tech. J. 24 (1): 46–156. https://doi.org/10.1002/j.1538-7305.1945.tb00453.x.
Rogers, T. T., and J. L. Mcclelland. 2014. “Parallel distributed processing at 25: Further explorations in the microstructure of cognition.” Cognit. Sci. 38 (6): 1024–1077. https://doi.org/10.1111/cogs.12148.
Roscoe, K., F. Diermanse, and T. Vrouwenvelder. 2015. “System reliability with correlated components: Accuracy of the Equivalent Planes method.” Struct. Saf. 57 (Nov): 53–64. https://doi.org/10.1016/j.strusafe.2015.07.006.
Royset, J. O., A. Der Kiureghian, and E. Polak. 2001. “Reliability-based optimal design of series structural systems.” J. Eng. Mech. 172 (6): 607–614. https://doi.org/10.1061/(ASCE)0733-9399(2001)127:6(607).
Rozvany, G. I. N. 2009. “A critical review of established methods of structural topology optimization.” Struct. Multidiscip. Optim. 37 (3): 217–237. https://doi.org/10.1007/s00158-007-0217-0.
Rubinstein, R. Y., and D. P. Kroese. 2013. The cross-entropy method: A unified approach to combinatorial optimization, Monte-Carlo simulation and machine learning. New York: Springer.
Rubinstein, R. Y., and D. P. Kroese. 2016. Simulation and the Monte Carlo method. New York: Wiley.
Schervish, M. J. 1984. “Algorithm AS 195: Multivariate normal probabilities with error bound.” J. R. Stat. Soc. Ser. C 33 (1): 81–94.
Schittkowski, K., C. Zillober, and R. Zotemantel. 1994. “Numerical comparison of nonlinear programming algorithms for structural optimization.” Struct. Optim. 7 (1–2): 1–19. https://doi.org/10.1007/BF01742498.
Schramm, U., H. L. Thomas, and M. Zhou. 2002. “Manufacturing considerations and structural optimization for automotive components.” In Proc., SAE Technical Paper 2002-01-1242. Warrendale, PA: SAE International.
Shinozuka, M. 1983. “Basic analysis of structural safety.” J. Struct. Eng. 109 (3): 721–740. https://doi.org/10.1061/(ASCE)0733-9445(1983)109:3(721).
Sigmund, O. 2009. “Manufacturing tolerant topology optimization.” Acta Mech. Sin. 25 (2): 227–239. https://doi.org/10.1007/s10409-009-0240-z.
Sigmund, O., and K. Maute. 2013. “Topology optimization approaches.” Struct. Multidiscip. Optim. 48 (6): 1031–1055. https://doi.org/10.1007/s00158-013-0978-6.
Son, Y. K., and G. J. Savage. 2007. “Set theoretic formulation of performance reliability of multiple response time-variant systems due to degradations in system components.” Qual. Reliab. Eng. Int. 23 (2): 171–188. https://doi.org/10.1002/qre.783.
Sonal, S. D., S. Ammanagi, O. Kanjilal, and C. S. Manohar. 2018. “Experimental estimation of time-variant system reliability of vibrating structures based on subset simulation with Markov chain splitting.” Reliab. Eng. Syst. Saf. 178 (Oct): 55–68. https://doi.org/10.1016/j.ress.2018.05.007.
Song, J., and A. Der Kiureghian. 2003. “Bounds on system reliability by linear programming.” J. Eng. Mech. 129 (6): 627–636. https://doi.org/10.1061/(ASCE)0733-9399(2003)129:6(627).
Song, J., and A. Der Kiureghian. 2006. “Joint first-passage probability and reliability of systems under stochastic excitation.” J. Eng. Mech. 132 (1): 65–77. https://doi.org/10.1061/(ASCE)0733-9399(2006)132:1(65).
Song, J., and W.-H. Kang. 2009. “System reliability and sensitivity under statistical dependence by matrix-based system reliability method.” Struct. Saf. 31 (2): 148–156. https://doi.org/10.1016/j.strusafe.2008.06.012.
Stahl, B., and J. F. Geyer. 1984. “Fatigue reliability of parallel member systems.” J. Struct. Eng. 110 (10): 2307–2323. https://doi.org/10.1061/(ASCE)0733-9445(1984)110:10(2307).
Stromberg, L. L., A. Beghini, W. F. Baker, and G. H. Paulino. 2012. “Topology optimization for braced frames: Combining continuum and beam/column elements.” Eng. Struct. 37 (Apr): 106–124. https://doi.org/10.1016/j.engstruct.2011.12.034.
Sudret, B., and A. Der Kiureghian. 2002. “Comparison of finite element reliability methods.” Probab. Eng. Mech. 17 (4): 337–348. https://doi.org/10.1016/S0266-8920(02)00031-0.
Sutradhar, A., G. H. Paulino, M. J. Miller, and T. H. Nguyen. 2010. “Topological optimization for designing patient-specific large craniofacial segmental bone replacements.” Proc. Nat. Acad. Sci. 107 (30): 13222–13227. https://doi.org/10.1073/pnas.1001208107.
Taflanidis, A. A., and J. L. Beck. 2009. “Stochastic subset optimization for reliability optimization and sensitivity analysis in system design.” Comput. Struct. 87 (5): 318–331. https://doi.org/10.1016/j.compstruc.2008.12.015.
Tang, L. K., and R. E. Melchers. 1986. “Improved approximation for multinormal integral.” Struct. Saf. 4 (2): 81–93. https://doi.org/10.1016/0167-4730(86)90024-X.
Tang, L. K., and R. E. Melchers. 1987. “Dominant mechanisms in stochastic plastic frames.” Reliab. Eng. 18 (2): 101–115. https://doi.org/10.1016/0143-8174(87)90025-4.
Terlaky, T. 1998. “Optimization. Algorithms and consistent approximations: Elijah Polak Springer, New York, NY, 1997, ISBN 0-38794971-2, hb., 118 DM, 779 pages.” Eur. J. Oper. Res. 107 (3): 755–756. https://doi.org/10.1016/S0377-2217(98)80004-0.
Thampan, C. K. P. V., and C. S. Krishnamoorthy. 2001. “System reliability-based configuration optimization of trusses.” J. Struct. Eng. 127 (8): 947–956. https://doi.org/10.1061/(ASCE)0733-9445(2001)127:8(947).
Thoft-Christensen, P., and Y. Murotsu. 2012. Application of structural systems reliability theory. New York: Springer.
Tu, J., K. K. Choi, and Y. H. Park. 1999. “A new study on reliability-based design optimization.” J. Mech. Des. 121 (4): 557–564. https://doi.org/10.1115/1.2829499.
Valdebenito, M. A., and G. I. Schuëller. 2011. “Efficient strategies for reliability-based optimization involving non-linear, dynamical structures.” Comput. Struct. 89 (19–20): 1797–1811. https://doi.org/10.1016/j.compstruc.2010.10.014.
Vanmarcke, E. H. 1975. “On the distribution of the first-passage time for normal stationary random processes.” J. Appl. Mech. 42 (1): 215–220. https://doi.org/10.1115/1.3423521.
Verma, A. K., S. Ajit, and D. R. Karanki. 2010. Reliability and safety engineering. London: Springer.
Wang, Z., and J. Song. 2016. “Cross-entropy-based adaptive importance sampling using von Mises-Fisher mixture for high dimensional reliability analysis.” Struct. Saf. 59 (Mar): 42–52. https://doi.org/10.1016/j.strusafe.2015.11.002.
Yang, K., and H. Younis. 2005. “A semi-analytical Monte Carlo simulation method for system’s reliability with load sharing and damage accumulation.” Reliab. Eng. Syst. Saf. 87 (2): 191–200. https://doi.org/10.1016/j.ress.2004.04.016.
Yu, S., Z. Wang, and D. Meng. 2018. “Time-variant reliability assessment for multiple failure modes and temporal parameters.” Struct. Multidiscip. Optim. 58 (4): 1705–1717. https://doi.org/10.1007/s00158-018-1993-4.
Yuan, X.-X., and M. D. Pandey. 2006. “Analysis of approximations for multinormal integration in system reliability computation.” Struct. Saf. 28 (4): 361–377. https://doi.org/10.1016/j.strusafe.2005.10.002.
Yun, W., Z. Lu, Y. Zhou, and X. Jiang. 2019. “AK-SYSi: An improved adaptive Kriging model for system reliability analysis with multiple failure modes by a refined learning function.” Struct. Multidiscip. Optim. 59 (1): 263–278. https://doi.org/10.1007/s00158-018-2067-3.
Zhang, X., L. Wang, and J. D. Sørensen. 2020. “AKOIS: An adaptive Kriging oriented importance sampling method for structural system reliability analysis.” Struct. Saf. 82 (Jan): 101876. https://doi.org/10.1016/j.strusafe.2019.101876.
Zhang, Y. C. 1993. “High-order reliability bounds for series systems and application to structural systems.” Comput. Struct. 46 (2): 381–386. https://doi.org/10.1016/0045-7949(93)90203-P.
Zhao, Y.-G., and T. Ono. 1998. “System reliability evaluation of ductile frame structures.” J. Struct. Eng. 124 (6): 678–685. https://doi.org/10.1061/(ASCE)0733-9445(1998)124:6(678).
Zou, T., and S. Mahadevan. 2006. “A direct decoupling approach for efficient reliability-based design optimization.” Struct. Multidiscip. Optim. 31 (3): 190–200. https://doi.org/10.1007/s00158-005-0572-7.
Information & Authors
Information
Published In
Copyright
This work is made available under the terms of the Creative Commons Attribution 4.0 International license, https://creativecommons.org/licenses/by/4.0/.
History
Published online: Feb 16, 2021
Published in print: Jun 1, 2021
Discussion open until: Jul 16, 2021
Authors
Metrics & Citations
Metrics
Citations
Download citation
If you have the appropriate software installed, you can download article citation data to the citation manager of your choice. Simply select your manager software from the list below and click Download.
